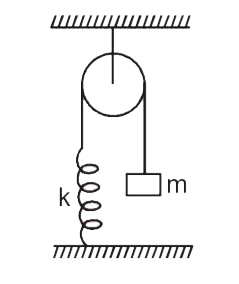
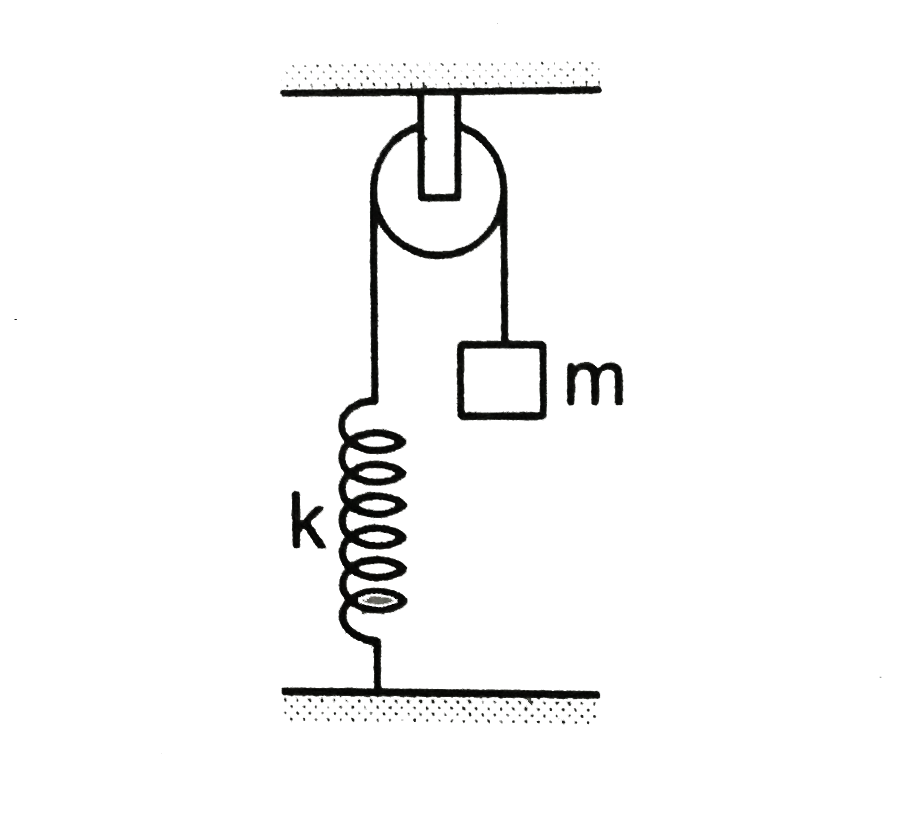
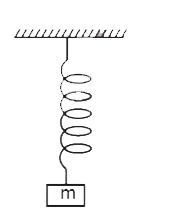
The string, spring and the pulley shown in figure are light. Find the time period of the mass m.

Force Method
Let in equilibrium position of the block, extension in spring is x0.
∴Kx0−1
Now if we displace the block by x in the downward direction, net force on the block towards mean position is
F=k(x+x0)−mg,=kx using (1)
Hence the net force is acting towards mean position and is also propotional to x. So, the particle will perform S.H.M. and its time period would be
T=2π√mk
(b) Energy Method
Let gravitational potential energy is to be zero at the level of the block when spring is in its natural length.
Now at a distance x below that level, let speed of the block be v.
Since total mechcanical energy is conserved in S.H.M.
∴−mgx+12kx2+12mv2=constant
Differentiating w.r.t. time, we get
−mgv+kxv+mva=0
where a is accleration.
∴F=ma=−kx+mg or F=−k(x−mgk)
This shows that for the motion, force constant is k and equilibrium position is x=mgk.
So, the particle will perform S.H.M and its timne period would be T=2π√mk
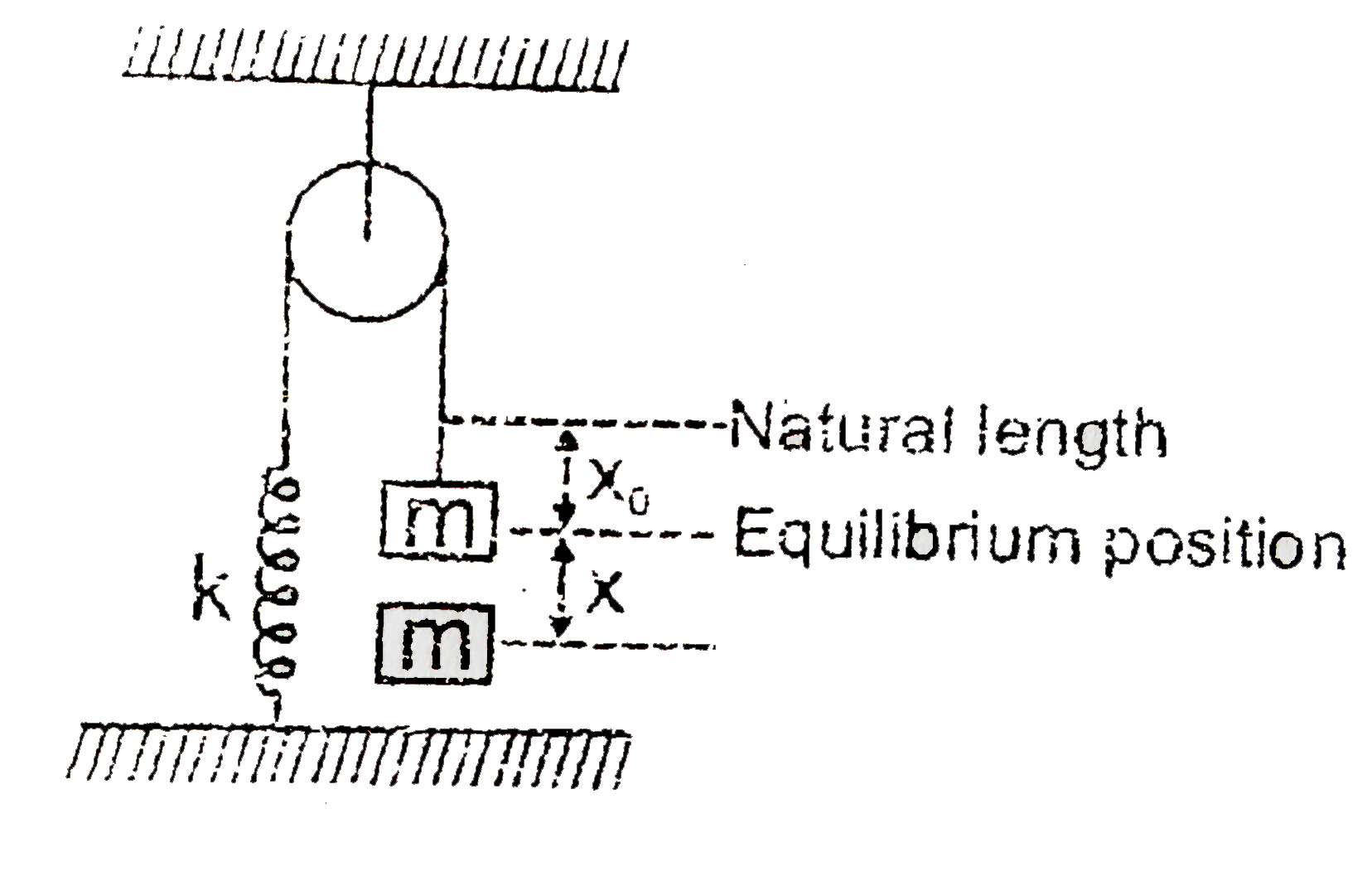
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems
9 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
Knowledge Check
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
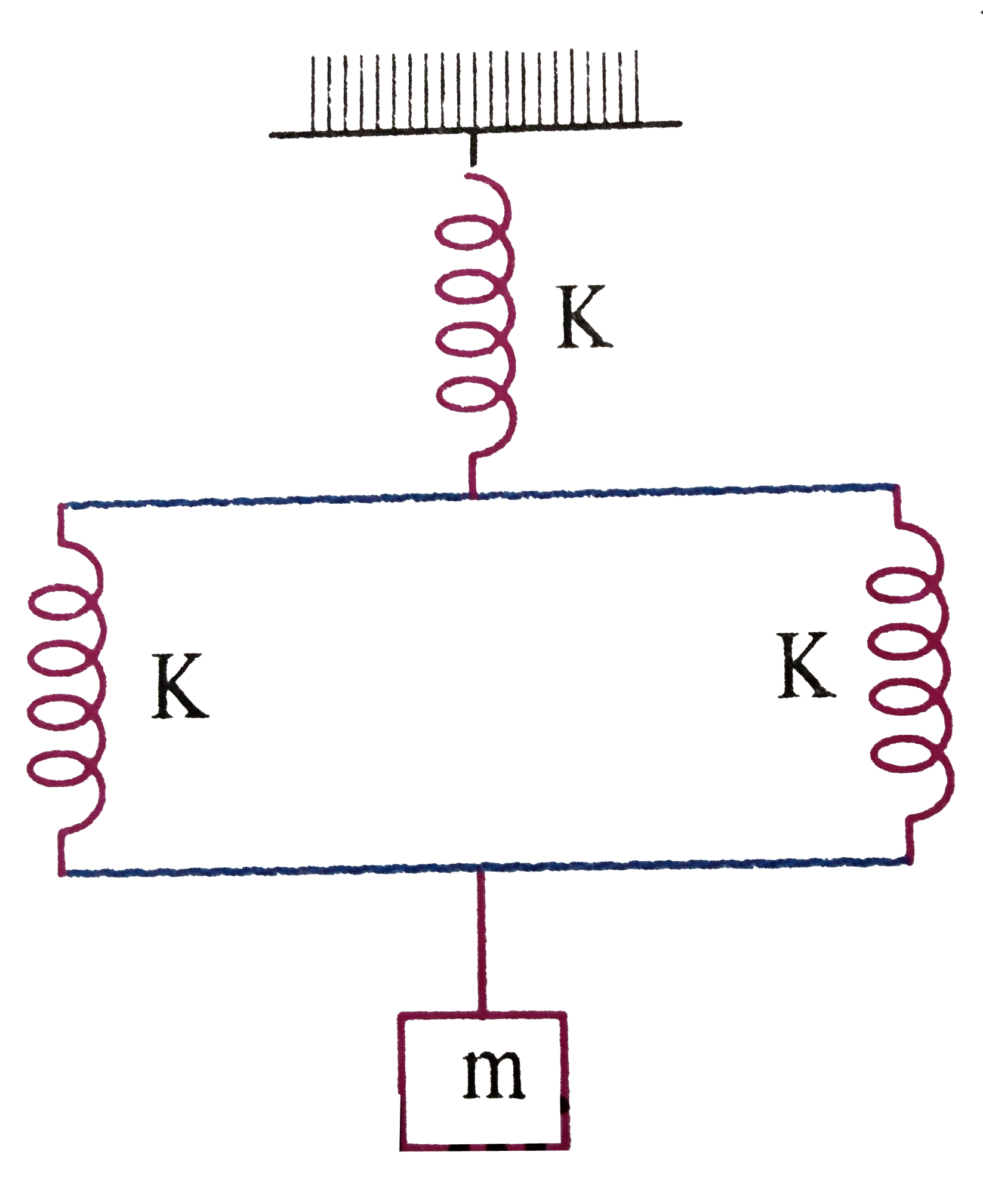 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.

View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionConsider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

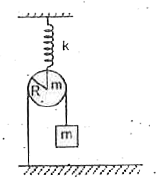
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
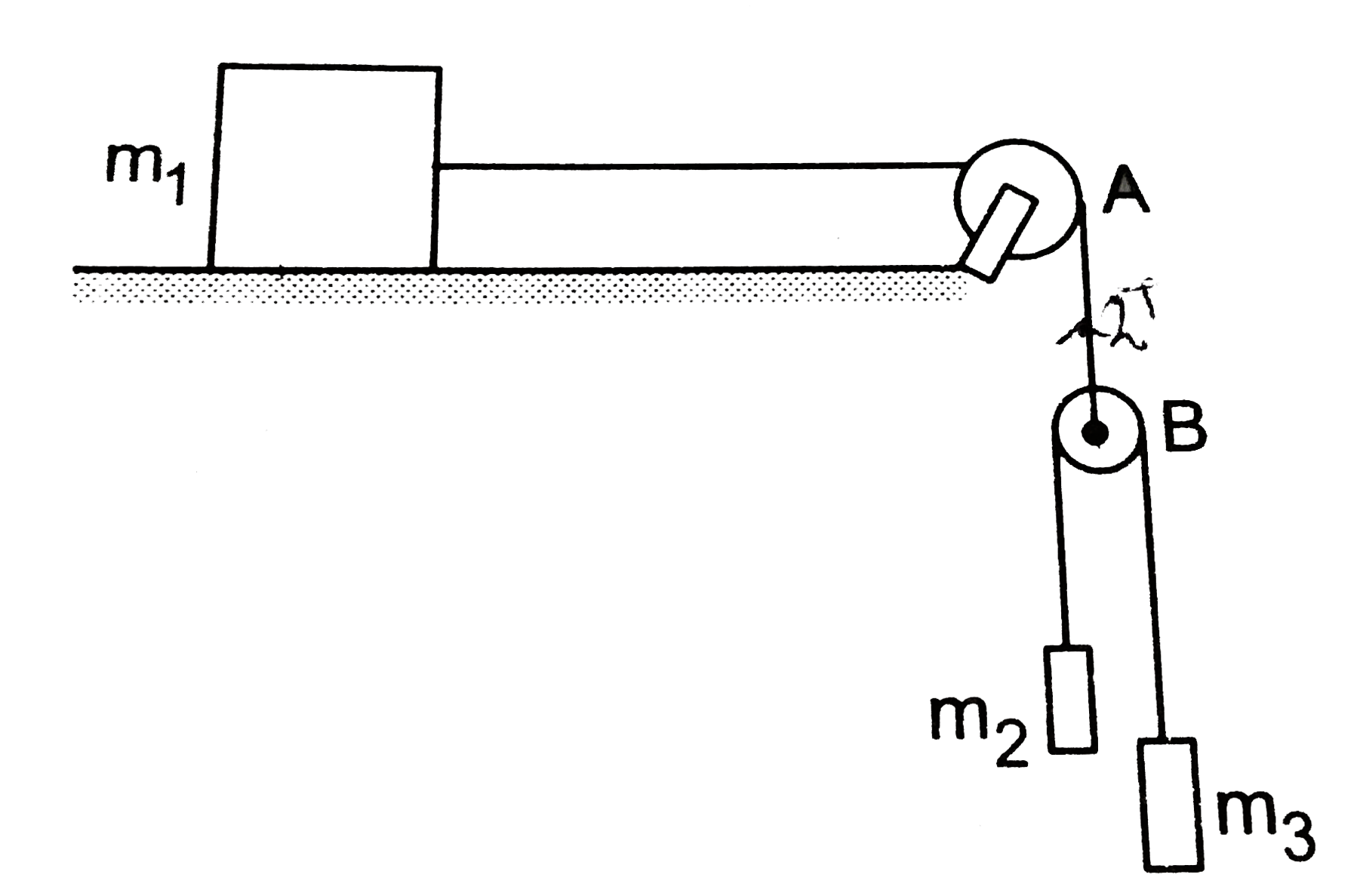
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
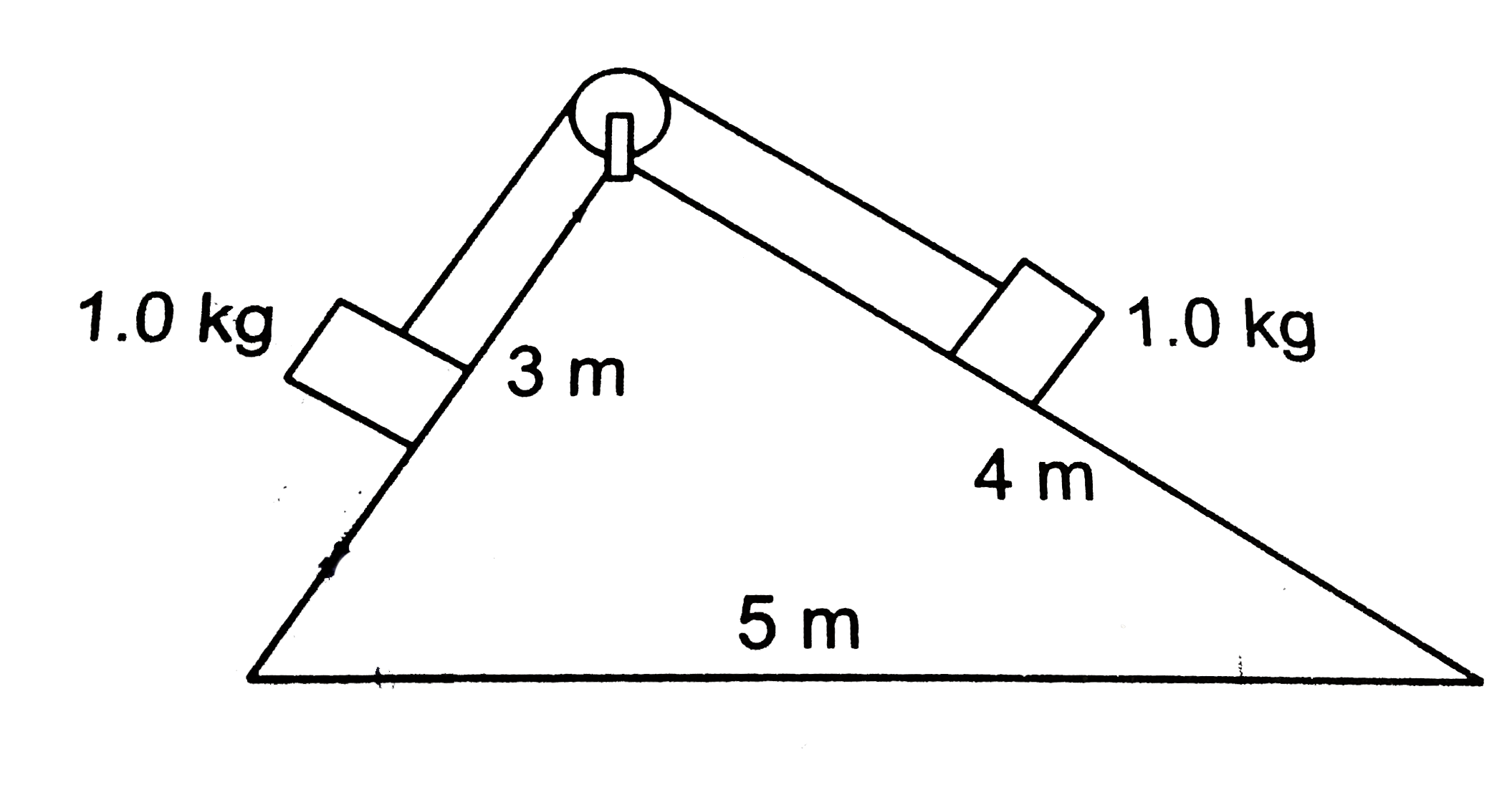
View SolutionA constant force F=m_2g/sisappliedontheblockofmassm_1asshown∈figure.Thestr∈gandthep≤––––yarelightandthesurfaceofthetab≤issm∞th.F∈dtheae≤rationofm_1
View Solution