A circuit contains an ideal cell and an inductor with a switch. Initially, the switch is open. It is closed at t=0. Find the current as a function of time.
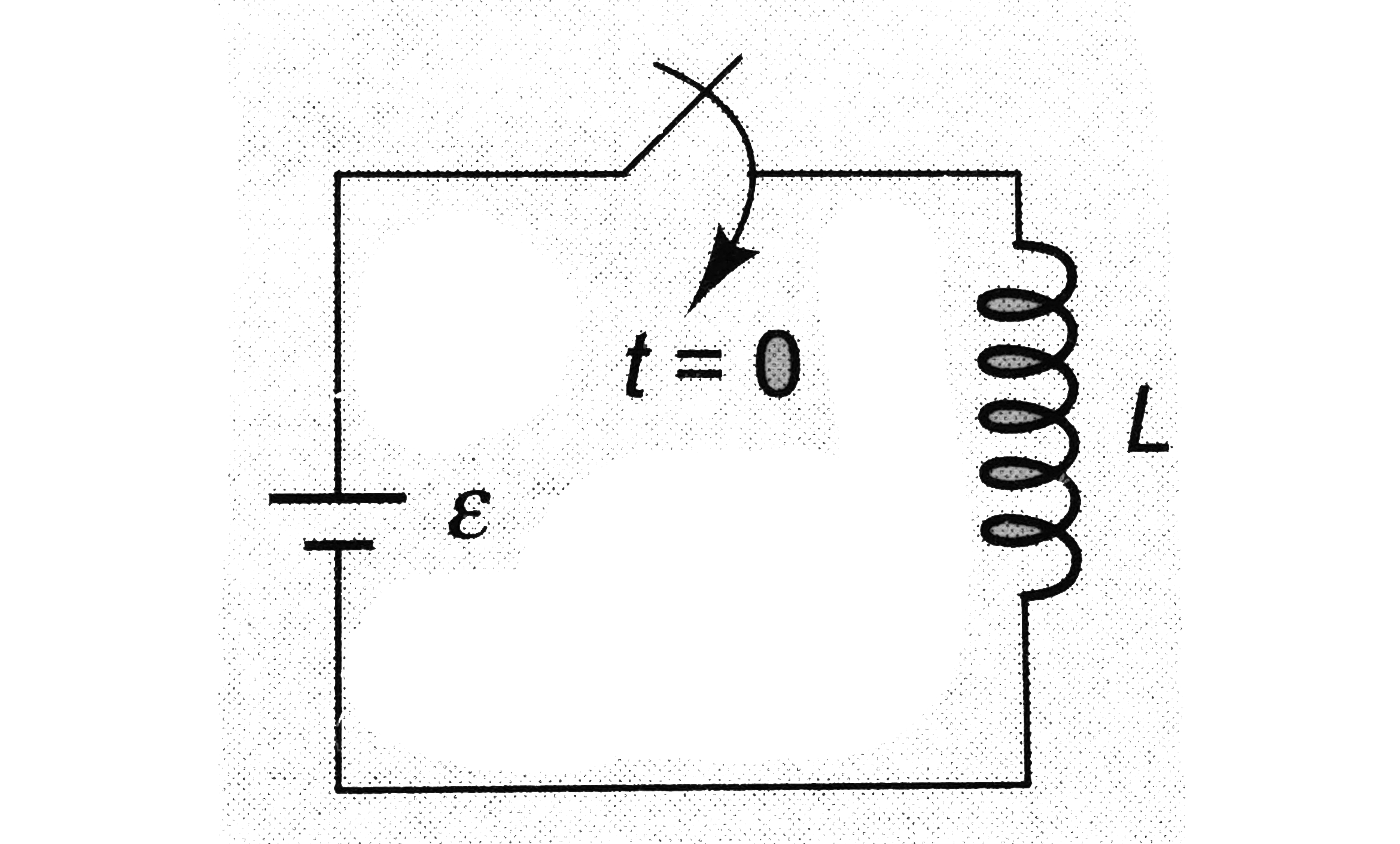
ε=Ldidt⇒i∫0εdt=i∫0εLdi
εt=Li⇒i=εtL
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Problem
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-1
Explore 63 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:HLP
Explore 39 Videos
Similar Questions
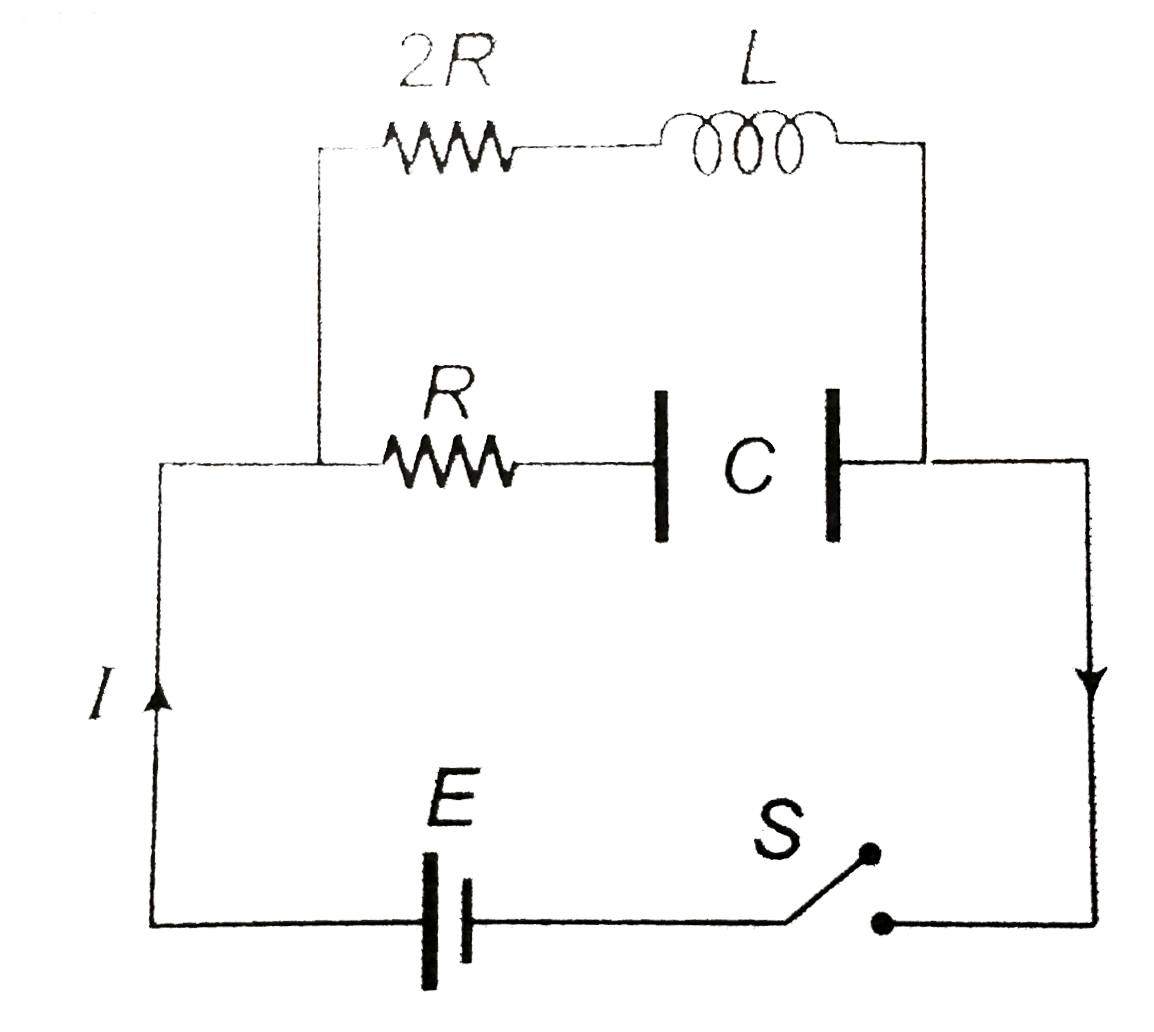
In the circuit diagram shown, intially there is no energy in the inductor and the capacitor. The switch is closed at t=0 . Find the current I as a function of time t .
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View Solution
Knowledge Check
An inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
AAt t = 0, induced emf in inductor is zeroBAt t=LR, energy stored in the inductor is (1−1e)2(LE22R2)CAt t=LR, induced emf in the inductor is EeDAt t=LR, voltage drop across the resistor is E(1−12)In the circuit shows in Fig the switch is closed at t=0.
 AAt t=0,I1=I2=0BAt any time t,I0I2=L2L1CAt any time t, I1+I2=εRDAt t=∞,I1 and I2 are independent of L1 and L2
AAt t=0,I1=I2=0BAt any time t,I0I2=L2L1CAt any time t, I1+I2=εRDAt t=∞,I1 and I2 are independent of L1 and L2
In given LR circuit the switch S is closed at time t=0 thenAThe ratio of induced emfs in the inductors of inductance L and 2L will be constantBThe ratio of induced emfs in the inductor of inductance L and 2L will be time varyingCthe potential difference VA−VB increases with timeDThe potential difference VA−VB will be constant
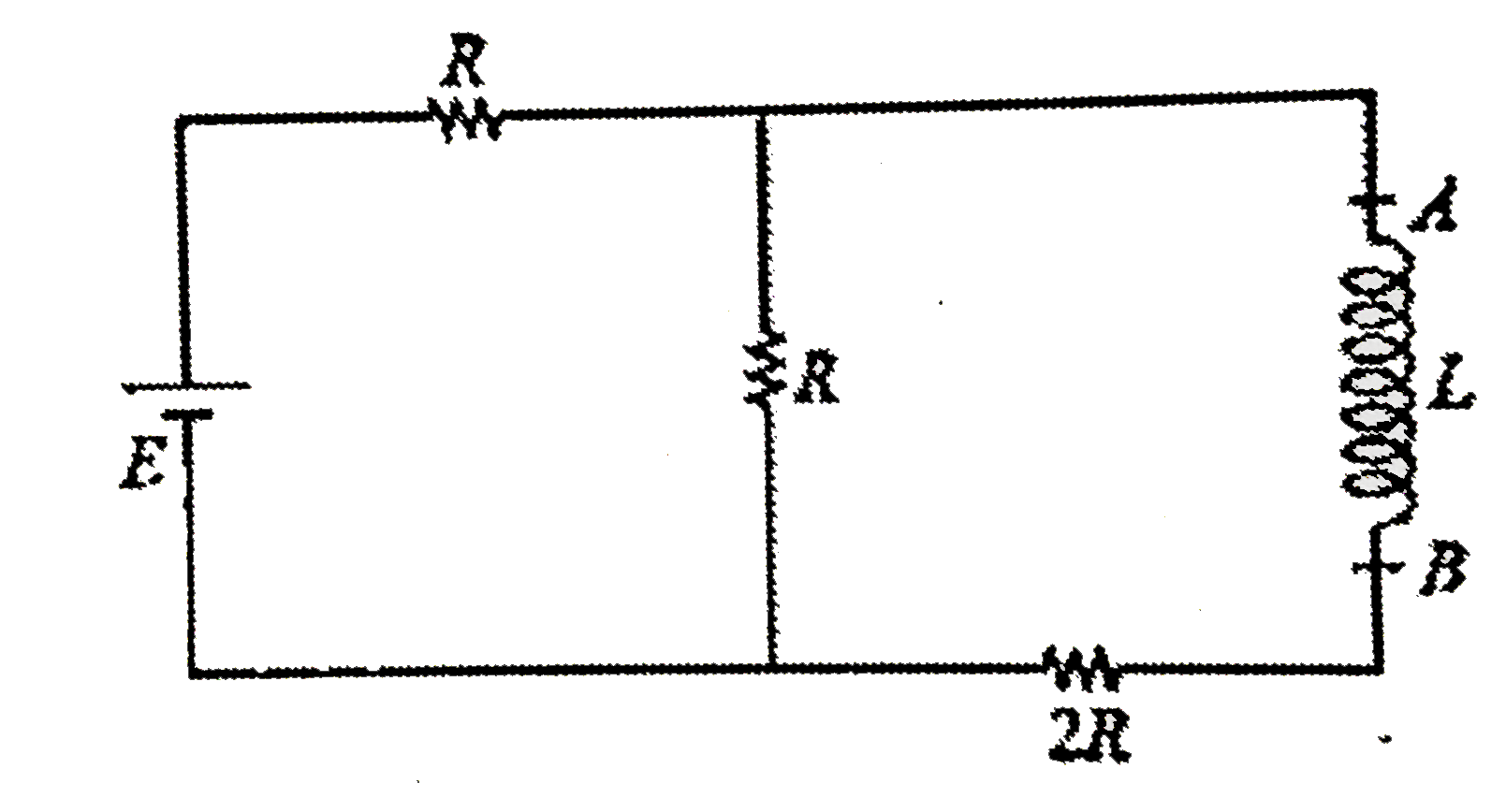
shows three resistances are
connected with switch S initially the switch is open. When
the switch S is closed find the current passed through it.
View SolutionFigure-5.102 shows a RL circuit. If at t-0 switch is closed, find the current in inductor as a function of time.
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

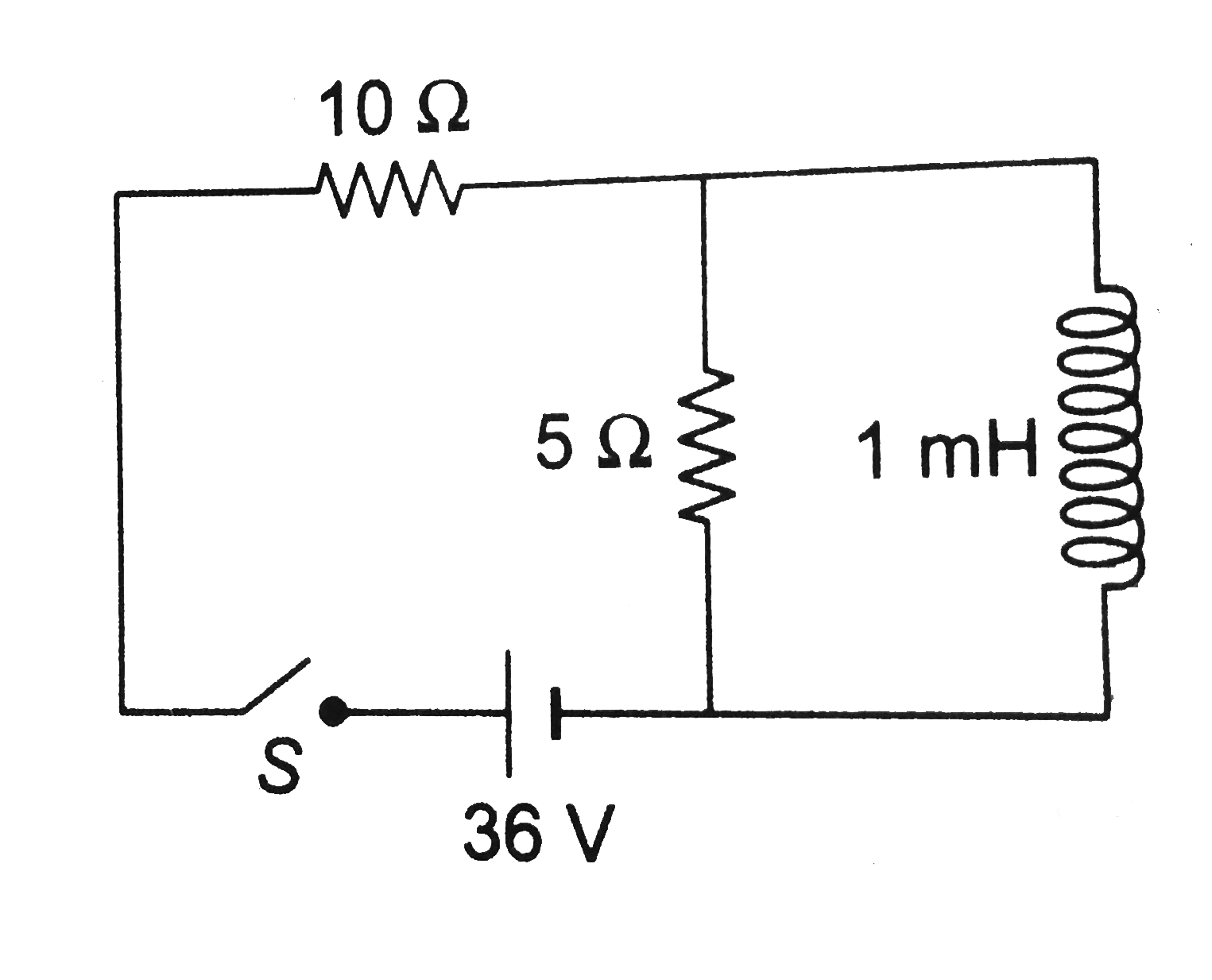
View SolutionIn the circuit arrangement shown in figure, the switch S is closed at t=0. Find the current in the inductance as a function of time? Does the current through 10Ω resistor vary with time or remains constant.
View Solution