Two capacitors of capacitances 2C and C are connected in series with an inductor of inductance L. Initially, capacitors have charge such that VB−VA=4V0 and VC−VD=V0. Initial current in the circuit is zero. Find
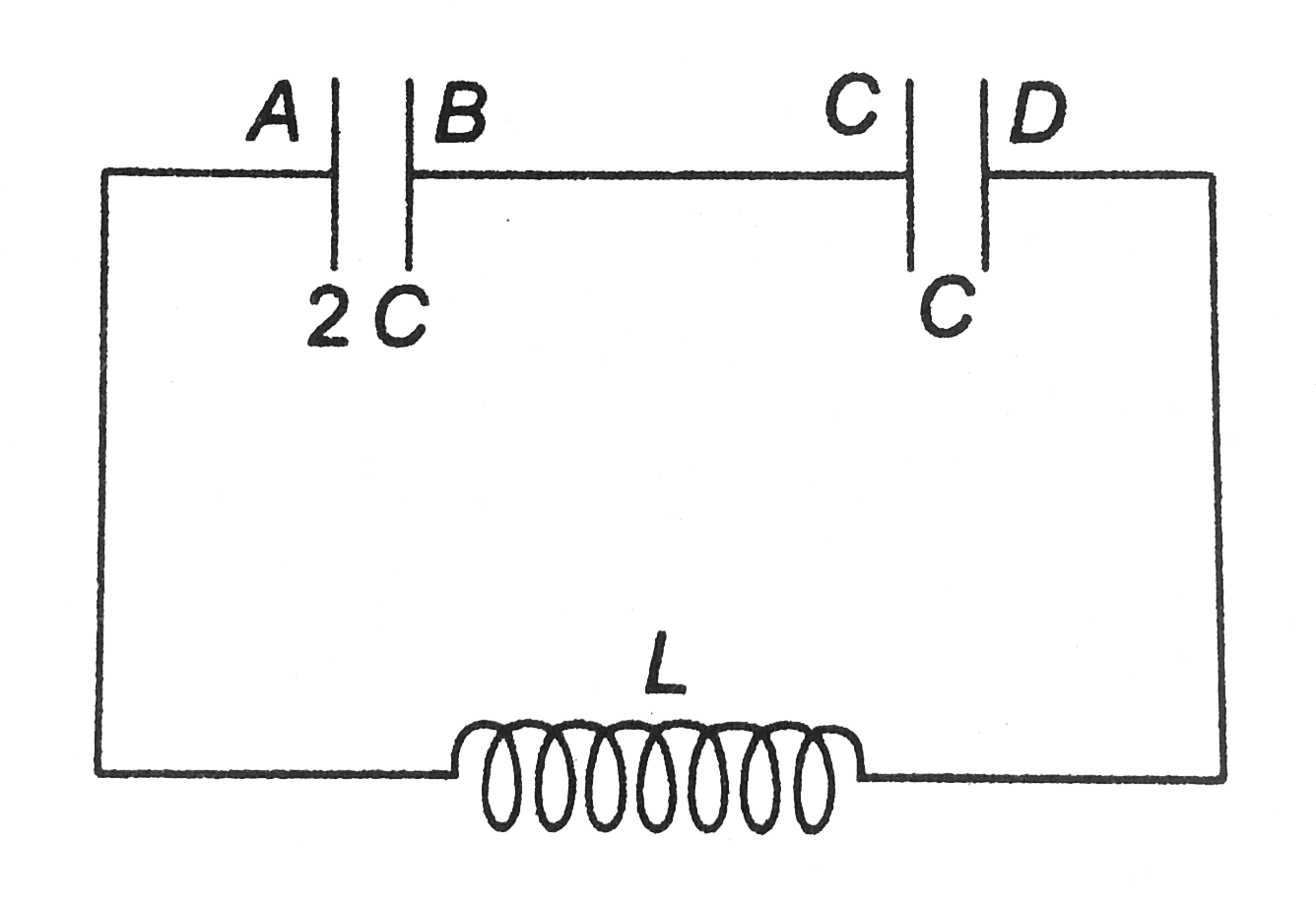
(a) maximum current that will flow in the circuit,
(b) potential difference across each capacitor at that instant,
(c) equation of current flowing towards left in the inductor.
The correct Answer is:A, B, C
The charges on both capacitors are shown at t=0sec.and any time t later in figure a and b.Applying KVL to the loop at any time when current i flows through it.
Ldidt+9CV0−Q2C−Q2C=0
for cuurent to be maximum didt=0 or Q=6CV0
Total energy in the system at t=0 is U=12L(0)2+12CV20=−Q2C+9CV0−QC=0 or Q=6CV0
Total energy in the system at t=0 is Ui=12L(0)2+12(2C)(4V0)2+12CV20=332CV20
Total energy when current i is maximum U1=12Limax2+12(6CV0)22C+12(3CV0)2C=12Limax2+272(6CV0)2
from conservation of energy 332CV20=12Limax2+272CV20,imax=√6CV20L
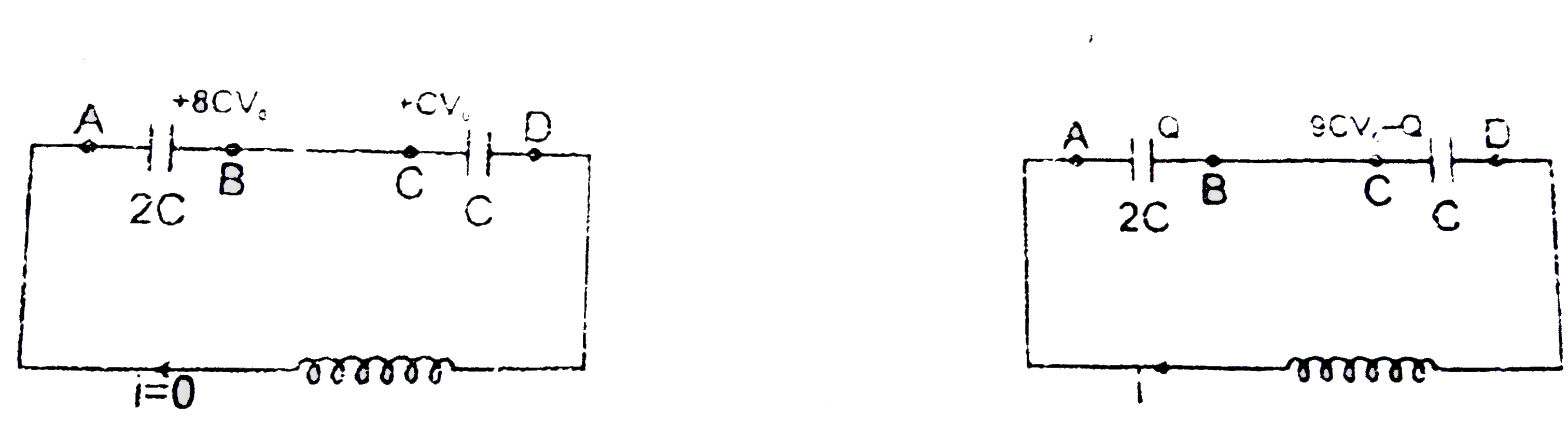
Topper's Solved these Questions
Similar Questions
Two capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionA capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. What is the current (in A) in the circuit at a time when the potential difference across the capacitor is 6.0V?
View Solution
Knowledge Check
In the circuit shown, the potential difference across the 3μF capacitor is V and the equivalent capacitance between A and B is C Then:
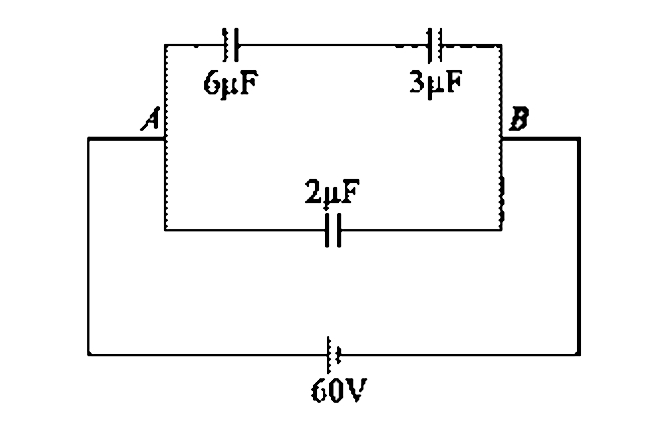 AC=4μFBC=11μFCV=20VDV=40V
AC=4μFBC=11μFCV=20VDV=40VTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
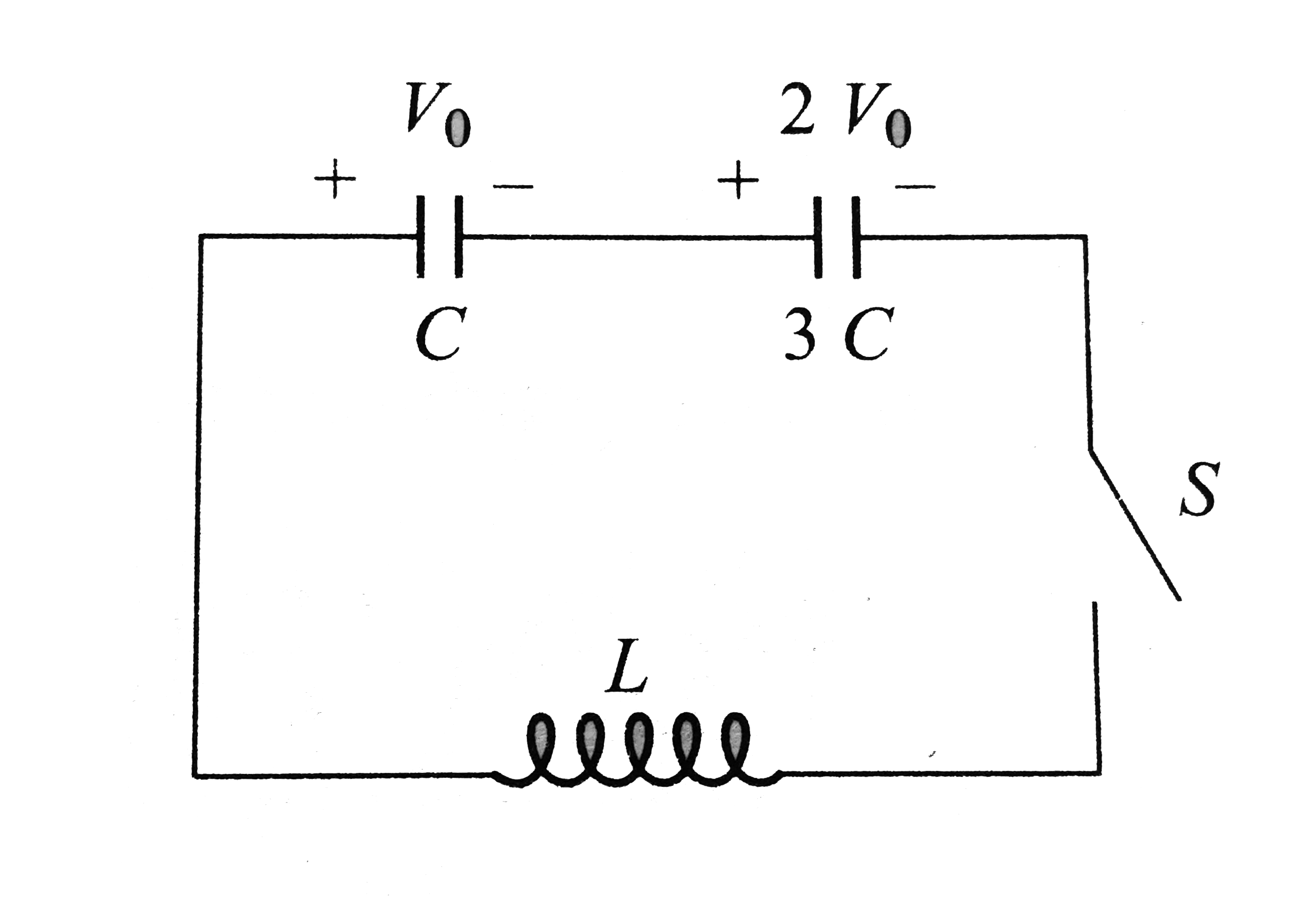
The maximum current in the inductor isA3V02√3CLBV0√3CLC2V0√3CLDV0√CLTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
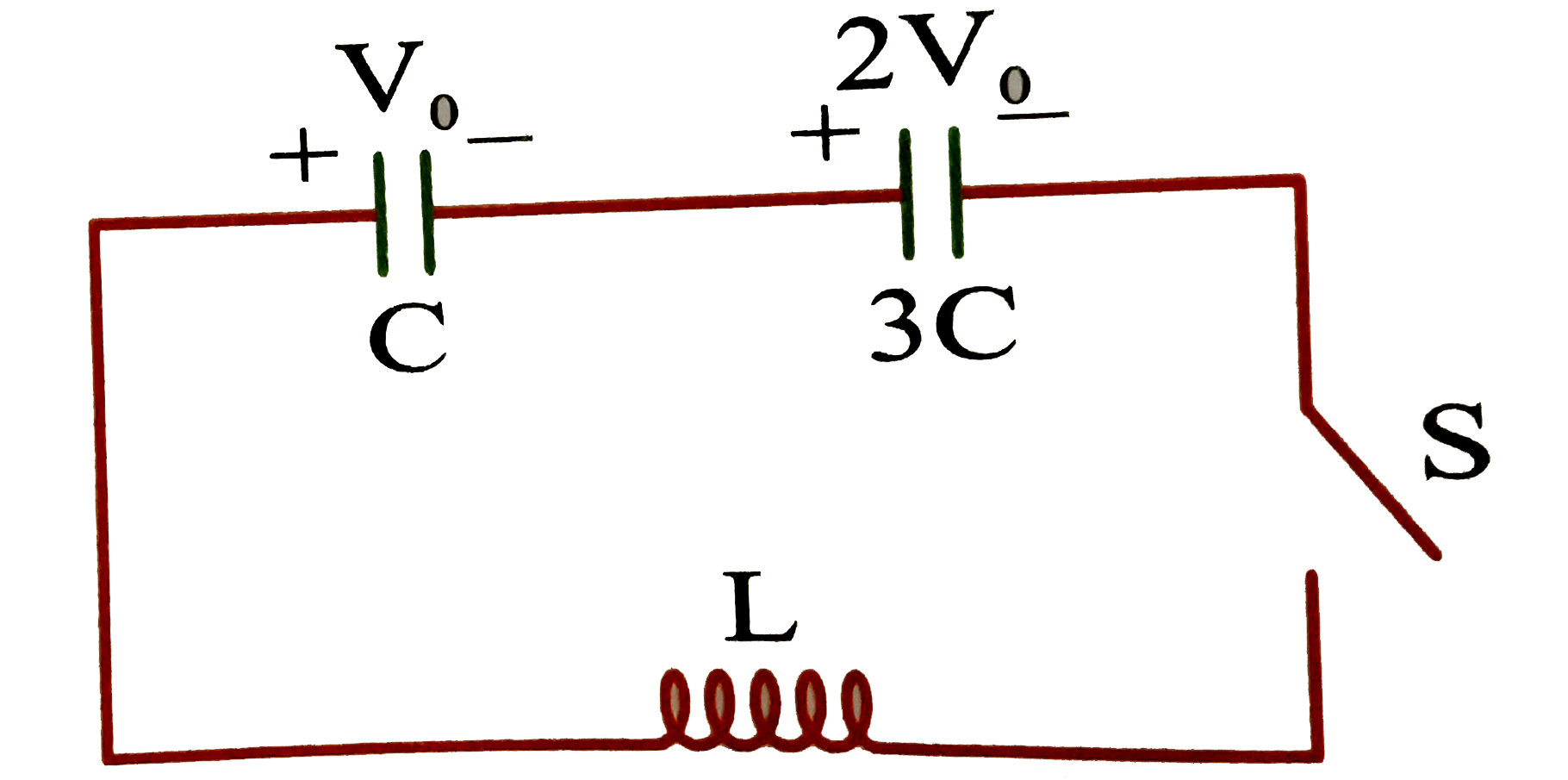
The maximum current in the indcutor is :A3V02√3CLBV0√3CLC2V0√3CLDV0√CL
Two capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
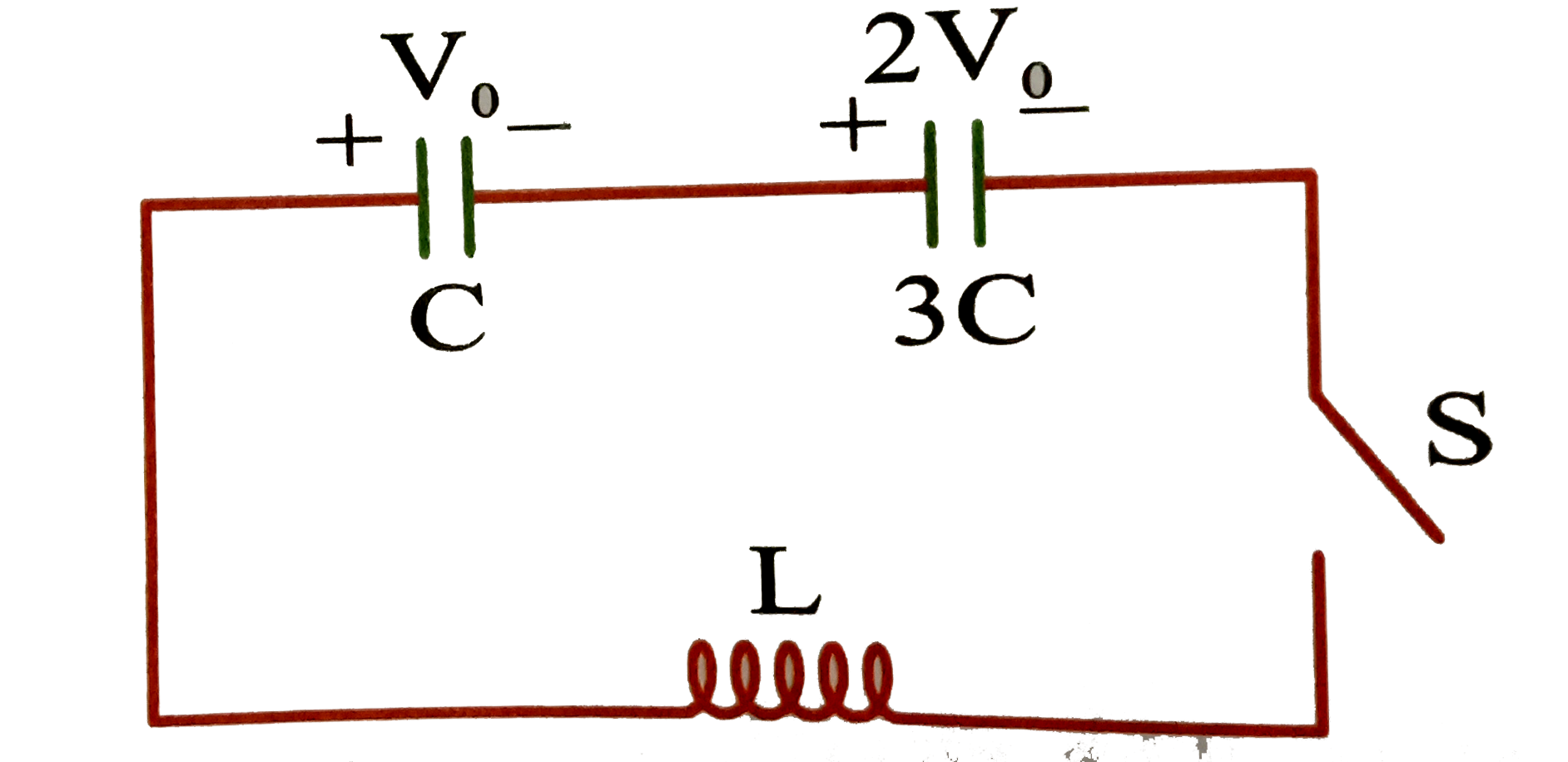
Potential difference across capacitor of capacitance C when the current in the cirucit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
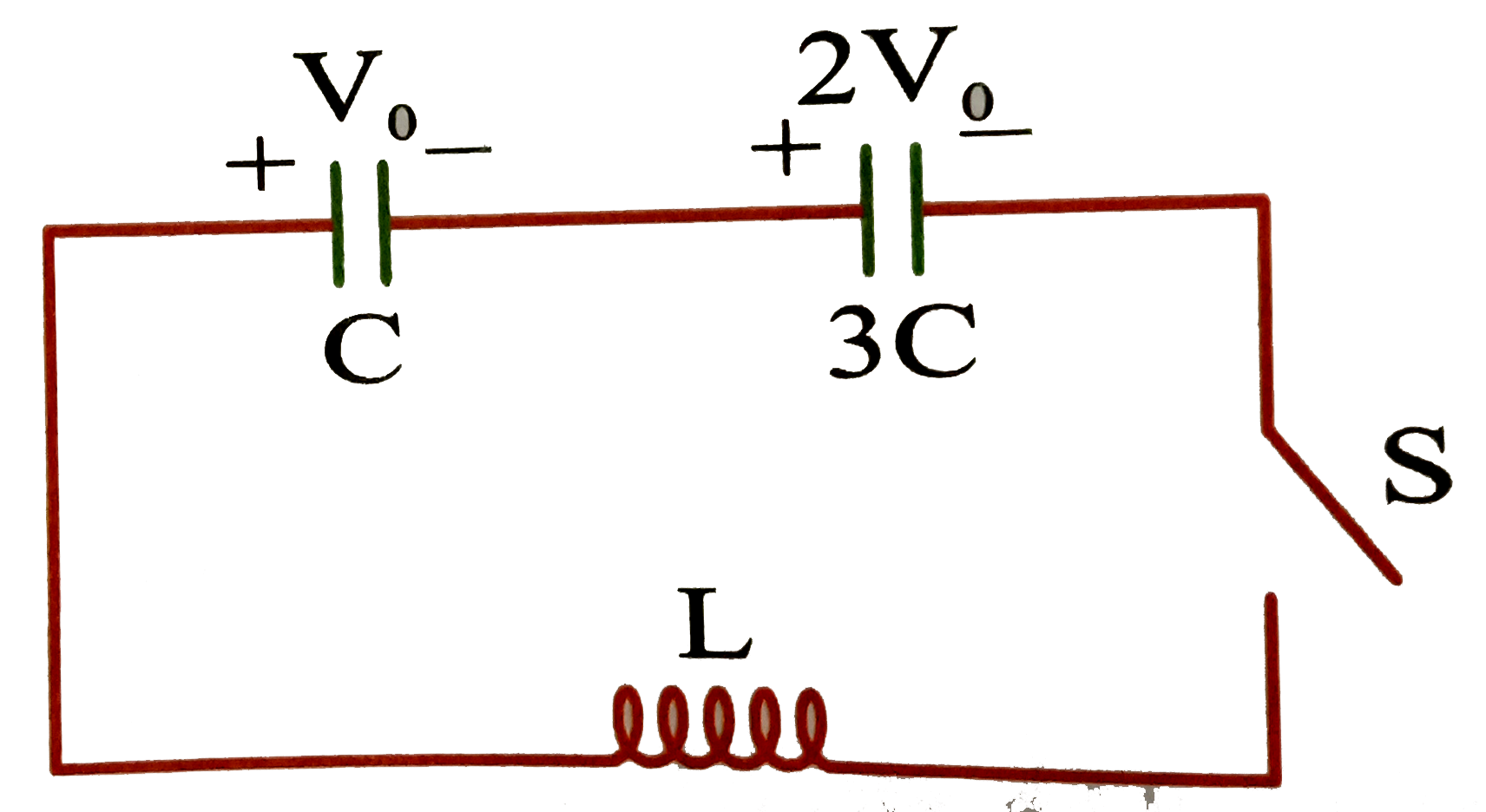
Potential difference across capacitor of capacitance 3C when the current in the cirucit is maximum is :
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
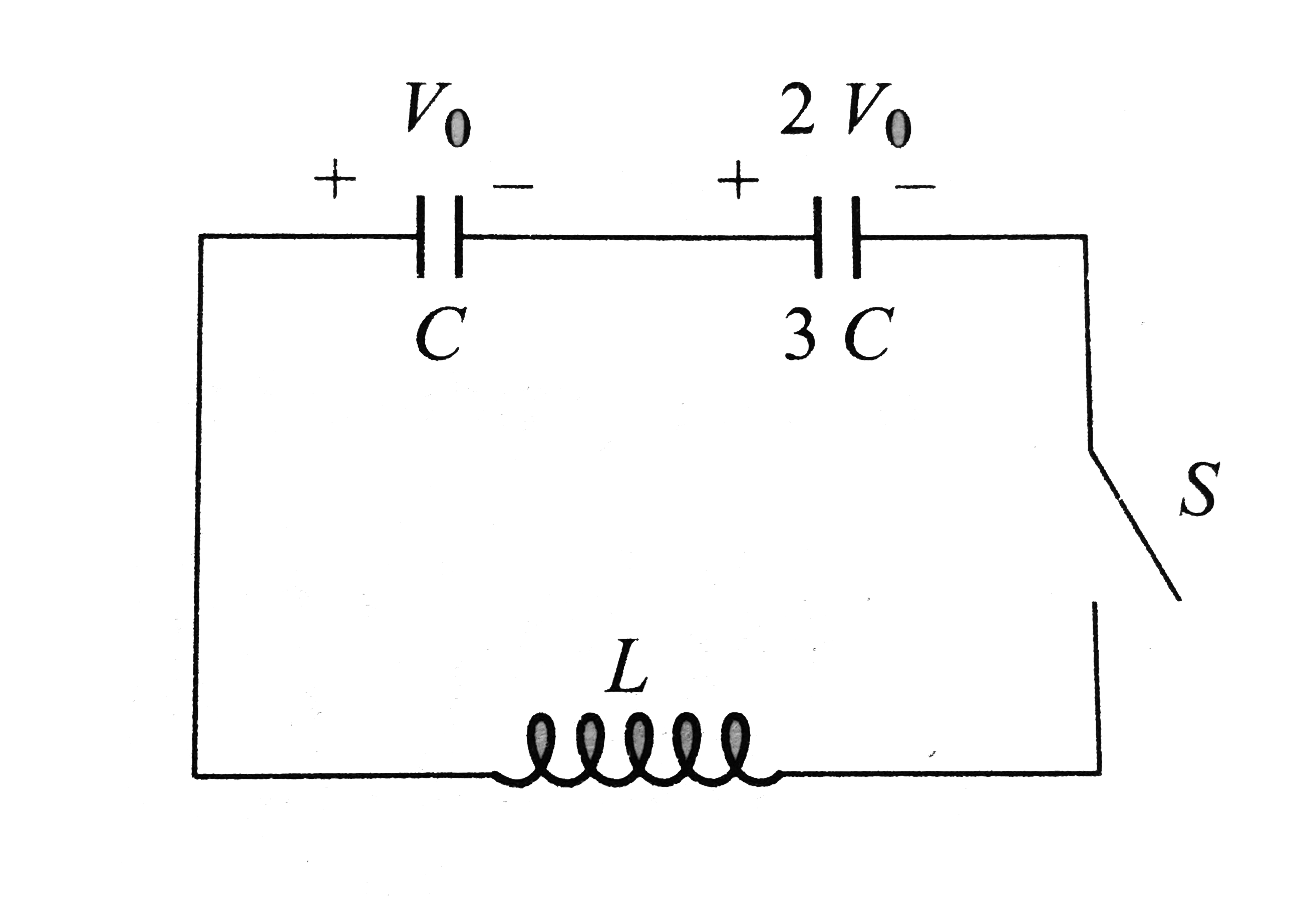
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
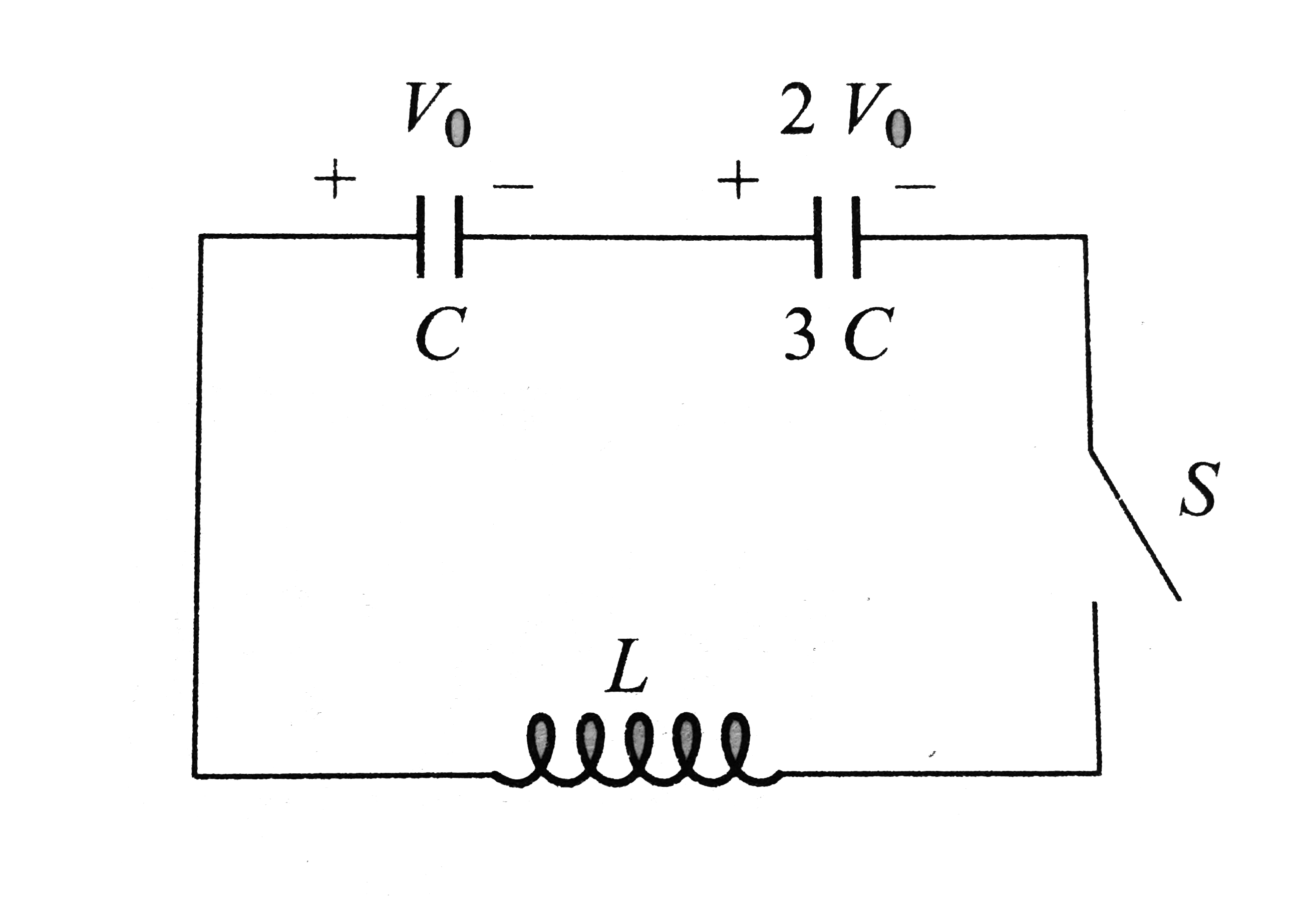
Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View Solution

