An infinitesimal bar magnet of dipole moment $M$ is pointing and moving with speed $v$ in the $x$ -direction. A closed circular conducting loop of radius a and negligible self-inductance lies in the $y - z$ plane with its centre at $x = 0$ and its axis coinciding with $x$ -axis. find the force opposing the motion of the magnet, if the resistance of the loop is $R$ . Assume that the distance $x$ of the magnet from the centre of the loop is much greater than a .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

Given that $x > > a$
magnetic field at the centre of the coil due to the bar magnet is $B = \frac{μ_{0}}{4 π} \frac{2 M}{x^{3}} = \frac{μ_{0}}{2 π} \frac{M}{x^{3}}$
Due to this, magnetic flux linked with the coil will be- $ϕ = B S = \frac{μ_{0}}{2 π} \frac{M}{x^{3}} (π a^{2}) = \frac{μ_{0} M a^{2}}{2 x^{3}}$
$∴$ induced $e m f$ in the coil, due to motion of the magnet is $e = \frac{- d ϕ}{d t} = - (\frac{μ_{0} M a^{2}}{2}) \frac{d}{d t} (\frac{l}{x^{3}})$
$= \frac{μ_{0} M a^{2}}{2} (\frac{3}{X^{4}}) \frac{d x}{d t} = \frac{3}{2} \frac{μ_{0} M a^{2}}{R x^{4}} V (\frac{d x}{d t} = V)$
Therefore, induced current in the coil is $i = \frac{e}{R} = \frac{3}{2} \frac{μ_{0} M a^{2} V}{R x^{4}}$
Potential energy of $\to M$ in $\to B$ will be $U = - M' B {cos 180}^{\circ}$
$U = M' B$
$= \frac{3}{2} \frac{μ_{0} π M a^{4} V}{R x^{4}} (\frac{μ_{0}}{2 π}, \frac{M}{x^{3}})$
$U = \frac{3}{4} \frac{μ_{0}^{2} M^{2} a^{4} V}{R} \frac{1}{x^{7}}$
$∴ F = - \frac{d U}{d x} = \frac{21}{4} \frac{μ_{0}^{2} M^{2} a^{4} V}{R x^{8}}$
Positive sign of $F$ implies that there will be a repulsion between the magnet and the coil. Note that here we cannot apply $F = \frac{μ_{0}}{4 π} \frac{6 M M'}{x^{4}}$ (directly)...(i)
because here $M$ is a funtion of $x$ however equation (1) can be applied where $M$ and $M'$ both are constants.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

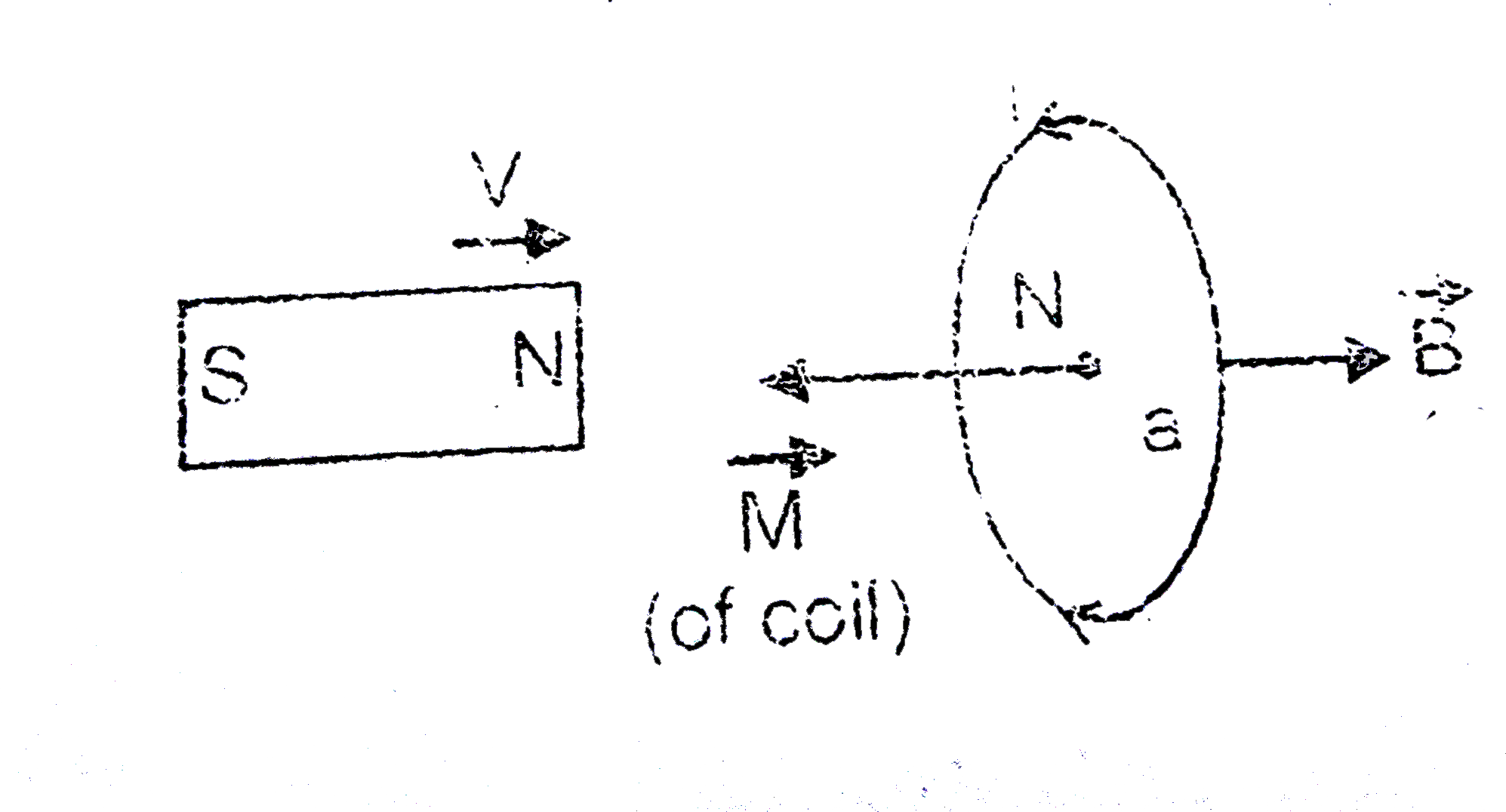
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The dipole moment of a short bar magnet is $1.25 A - m^{2}$ . The magnetic field on its axis at a distance of 0.5 metre from the centre of the magnet is
A $1.0 \times 10^{- 4} Newton / amp-meter$
B $4 \times 10^{- 2} Newton / amp-meter$
C $2 \times 10^{- 6} Newton / amp-meter$
D $6.64 \times 10^{- 8} Newton / amp-meter$
Question 2 - Select One
A circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.
Bzero
Cinversely proportional to r.
Ddirectly proportional to I.
Question 3 - Select One
A circular loop of radius R, carrying I lies in xy-plane with its centre at origin. The total magnetic flux through xy-plane is :
Adirectly proportional to R
Bdirectly proportional to I
Cinversely proportional to R
Dzero

RESONANCE-ELECTROMAGNETIC INDUCTION-A.l.P

Home
Ask Doubt
Profile