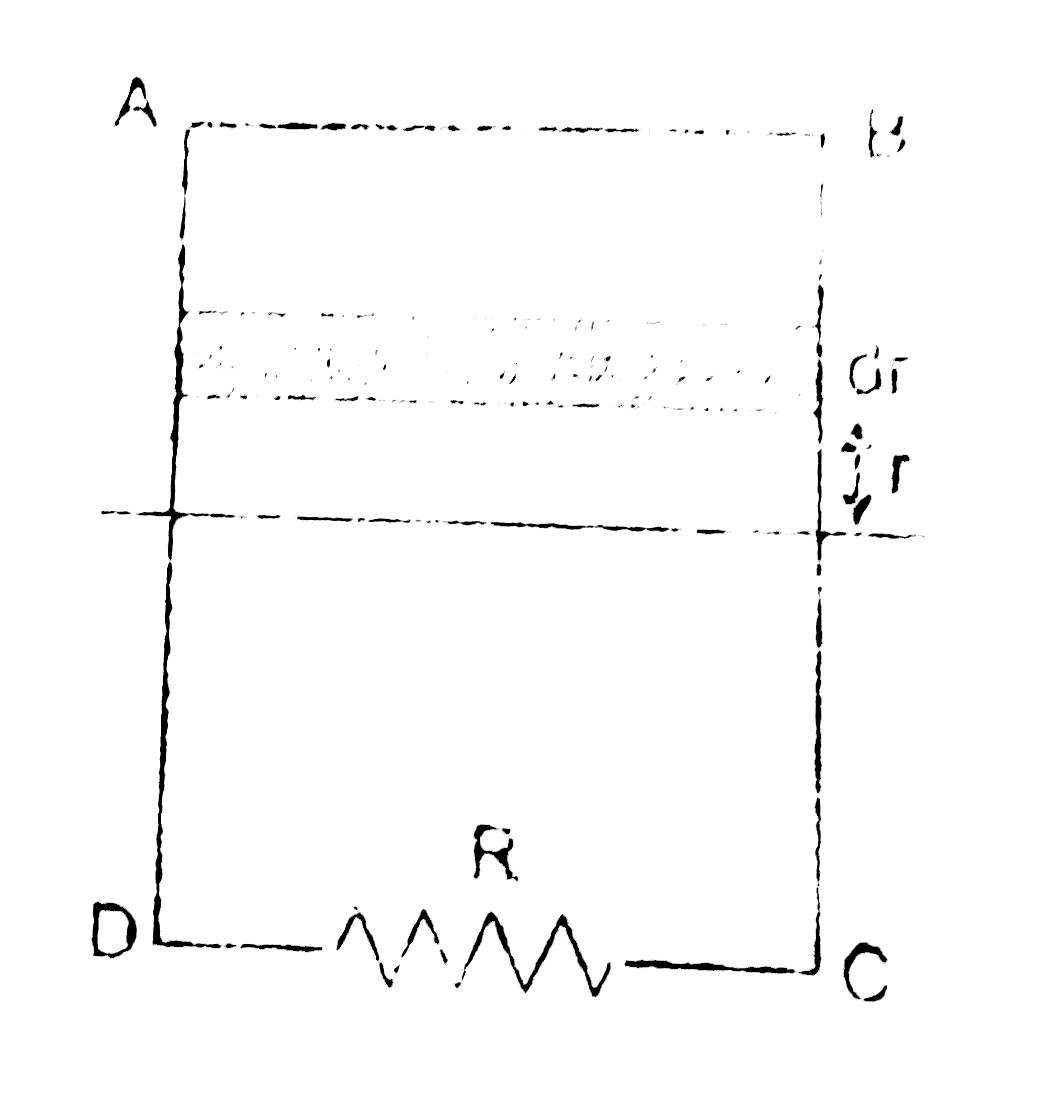
A square loop ABCD of side l is moving the xy plane with velocity →v=βtˆj.There exists a non-uniform magnetic field →B=−B0(1+αy2)ˆk(y>0), where B0 and α are positive constants. Initially, the upper wire of the loop is at y=0.Find the induced voltage across the resistance R as a function of time.Neglect the magnetic force due to induced current.
The correct Answer is:A, B, D
Flux inside the strip =B.l.dr ,=B0(1+ar2).Idr
Total flux in the loop =y∫0B0(1+ar2)Idtϕ=B0L(y+ay33)
Induced emfε=−dϕdt=−B0l(1+3ay33)dydt=−B0l(1+ay2)dydt
Given v=βt
dydt=βt y∫0dy−y∫0βtdt⇒y=l2
∴ε=−B0l(1+α×β2t54)βt⇒ε=−B0iβ(t−α×β2t54)
Topper's Solved these Questions
Similar Questions
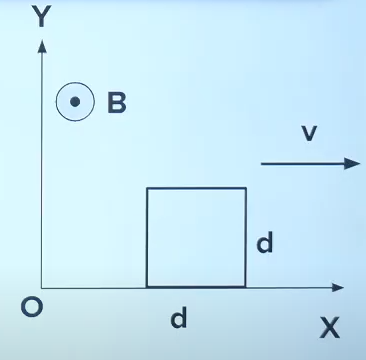
A square loop of side d is moved with velocity vˆi in an non-uniform magnetic field B0axˆk then the emf induced shown is?
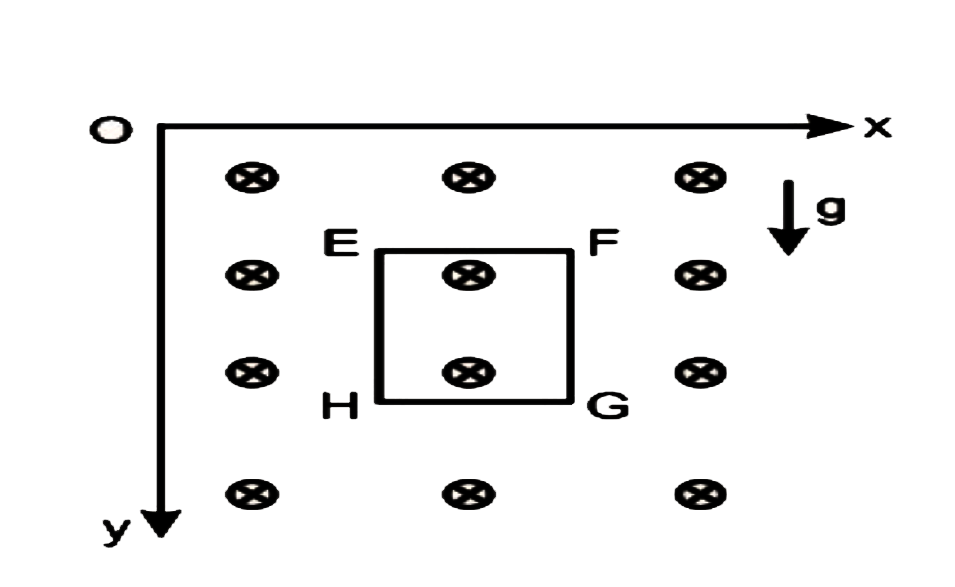
View SolutionA square loop EFGH of side a, mass m and total resistance R is falling under gravity in a region of transverse non - uniform magnetic field given by B=By0a =, where B0 is a positive constant and y is the position of side EF of the loop. If at some instant the speed of the loop is v, then the total Lorentz acting on the loop is
View Solution
Knowledge Check
- Question 1 - Select One
A proton is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj.
Aits z-coordinate can never be negativeBits x-coordinate can never be negativeCits x-and z-coordinates cannot be zero at the same timeDits y-coordinate will be proportional to its time of flight - Question 2 - Select One
An electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
Aremains constantBincreases with timeCdecreases with timeDincreases and decreases periodically - Question 3 - Select One
A square loop of side 'a' is placed in x−y plane as shown in figure. In this region there is non-uniform time dependent magnetic field →B=(cy3t2)→k, [where t is time and c is constant] then magnitude of emf induced in loop is
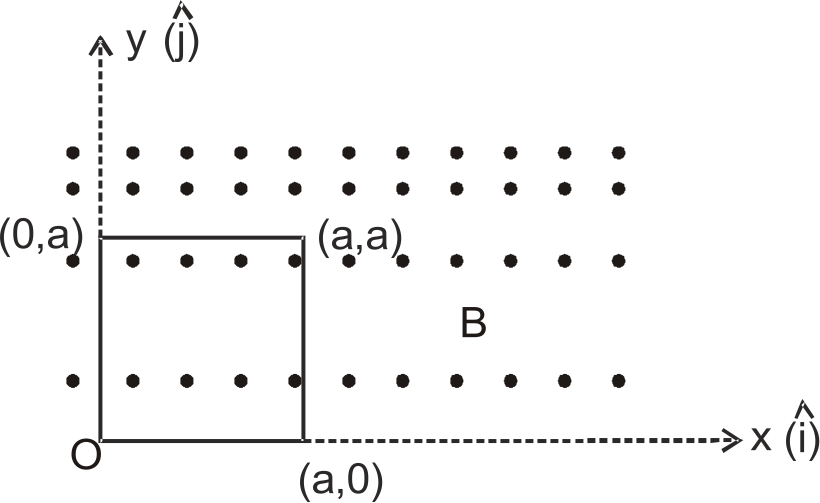AZeroBca4t25Cca5t2Ddata is insufficient
There exists a uniform magnetic field ¯¯¯B=B0t¯k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
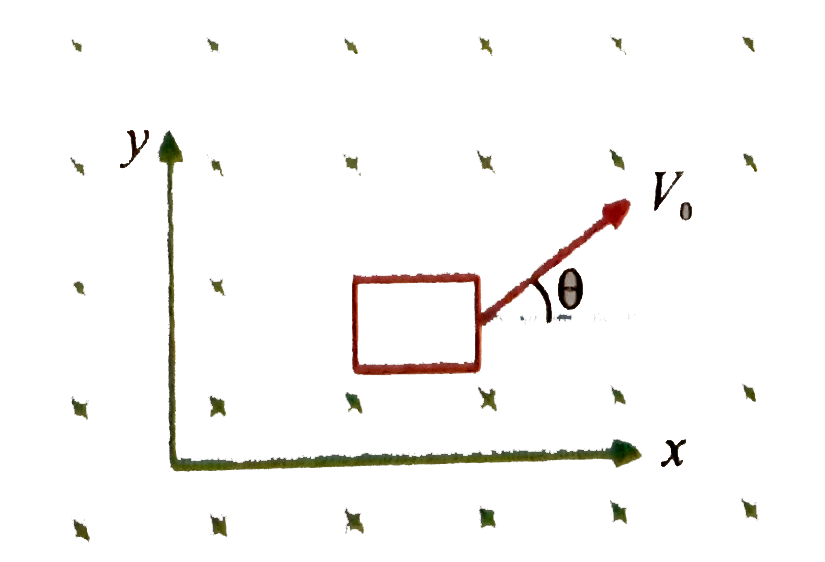
View SolutionIn the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is
View SolutionA conducting square loop PQRS of side L and resistance R moves in its plane with a uniform velocity vcev perpendicular to one of its sides. A magnetic field vceB, constant in time and space, pointing perpendicular and out of the plane of loop exists everywhere.
The current induced in the loop is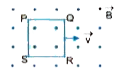
View SolutionA square of side L metre lies in the x - y plane in a region, where the magnetic field is given by →B=B0(2ˆi+3ˆj+4ˆk)T, where B0, is constant. The magnitude of flux passing through the square is [Exemplar Problem]
View Solution