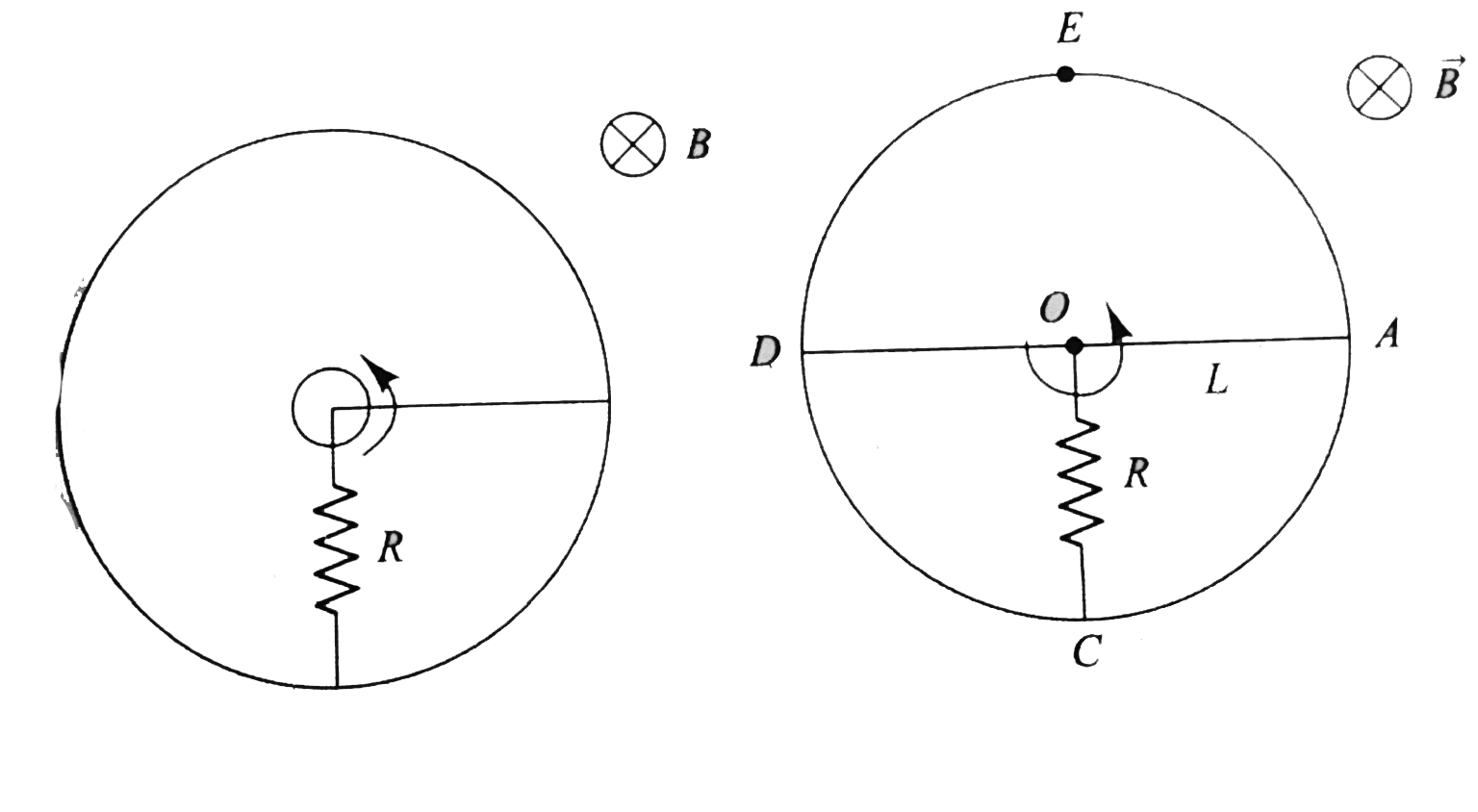
Solve the above question if the length of rod is 2L and resistance 2r and it is rotating about its centre.Both ends of the rod now touch the conductiing ring
i=εR+r2=12BωL2R+r2

Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP
39 Videos
Similar Questions
Solve problem 15 if the length of rod is 2L and resistance 2r and it is rotating about its center. Both ends of the rod now touch the conducting ring.
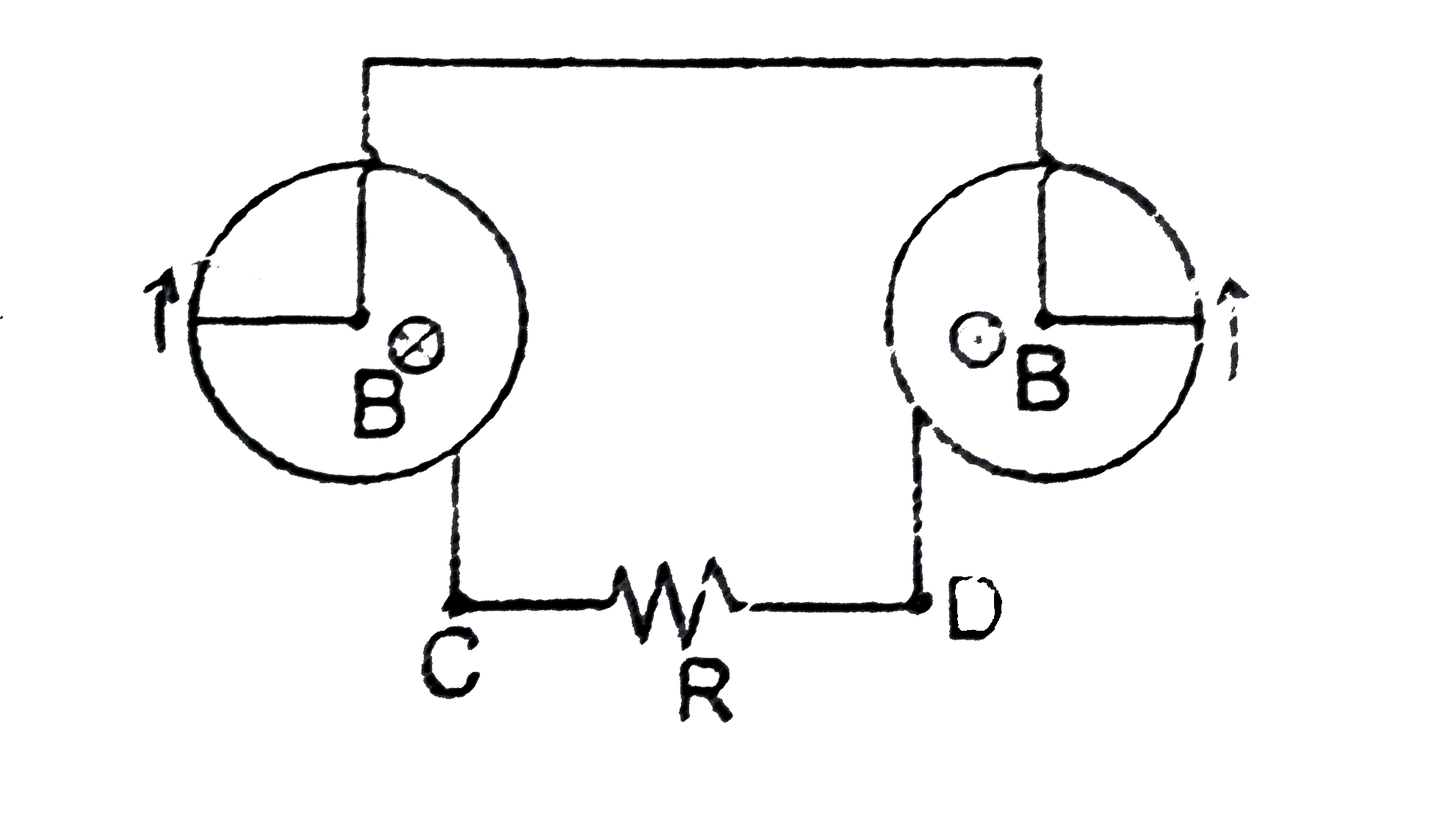
View SolutionIn the figure there are two identical conducting rods each of length a rotating with angular speed ω is the direction shown.One end of each rod touches a conducting ring.Magnetic field B exists perpendicular to the plane of the rings.The rods the conducting rings and the lead wires and resistanceless.Find the magnitude and direction of current in the resistance R.
View Solution
Knowledge Check
A cylindrical copper rod has length L and resistance R. If it is melted and formed into another rod of length 2L, the resistance will be
ARB2RC4RD8RA metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
 ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseB
ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseBA rod having length L, density D and area of Cross-section A is rotating about the centre with velocity @ and perpendicular to its length. Its rotational kinetic energy is
A13DAL3ω2B112DAL3ω2C124DAL3ω2D16DAL3ω2
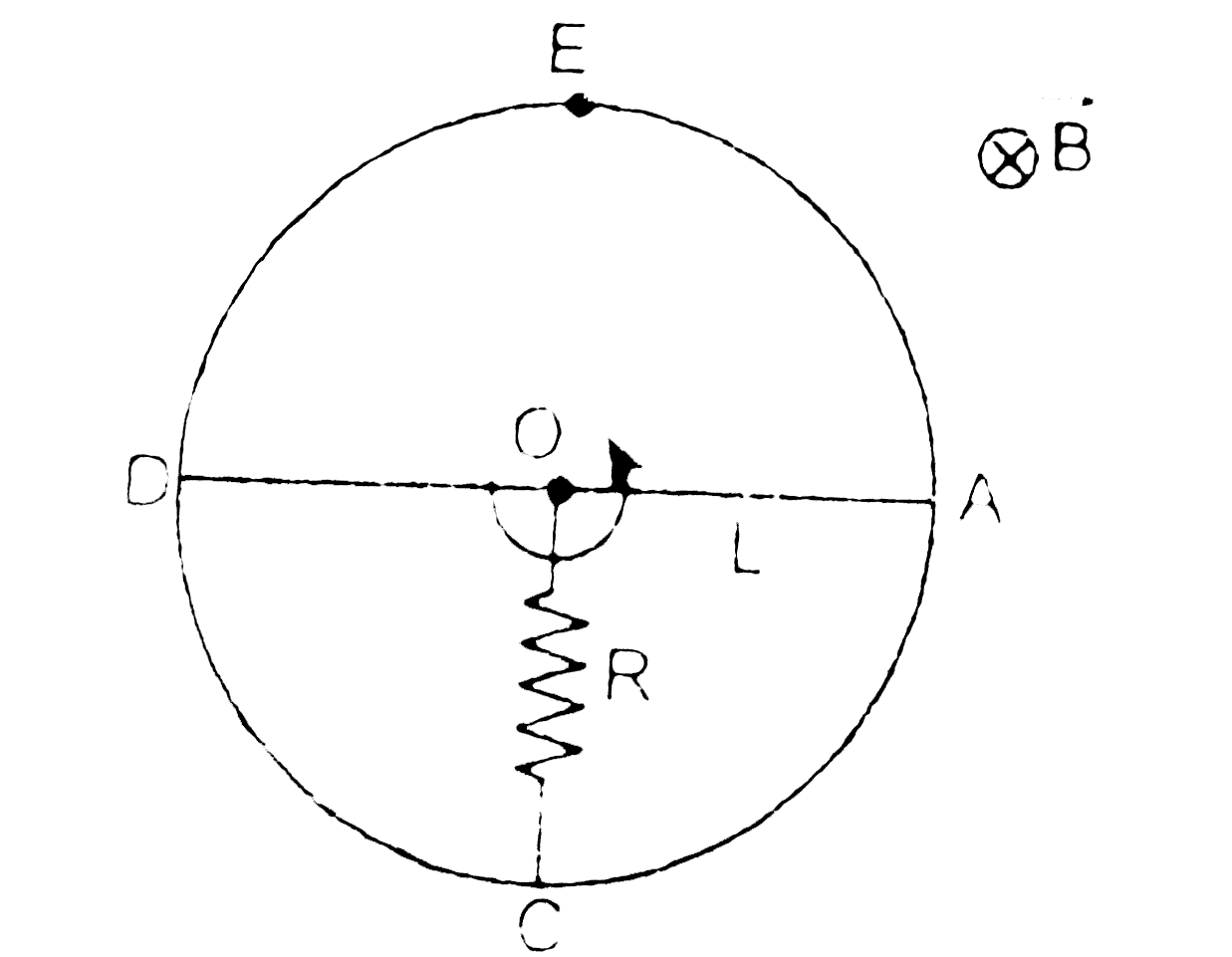
A rod of length L and resistance r rotates about one end as shown in . Its other end touches a conducting ring of negligible resistence. A resistence R is connected between the center and periphery. Draw the electrical equivalence and find the current in resistance R. There is a uniform magnetic field B directed as shown in .
View SolutionOne end of a metal rod of length L and mass M is pivoted to a fixed support and to its free end, a thin disc of mass m and radius r (L) is attached at its centre. In one case, the disc is attached to the rod in such a way that it is not free to rotate about its centre and in another case, teh disc is free to rotate about its centre. When the rod-disc system is displaced slightly from its equilibrium position and released. it peforms S.H.M. in vertical plane. Compare the restoring torque acting on the system and angular frequency in both the cases.
View SolutionA rod of length l and resistance r rotates about one end as shown in figure.Its othr end touches a conducting ring a of negligible resistance.A resistance R is connected between centre and periphery.Draw the electrical equivalence and find the current in the resistance R.There is a uniform magnetic field B directed as shown.

View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .
.
View Solution
