Question

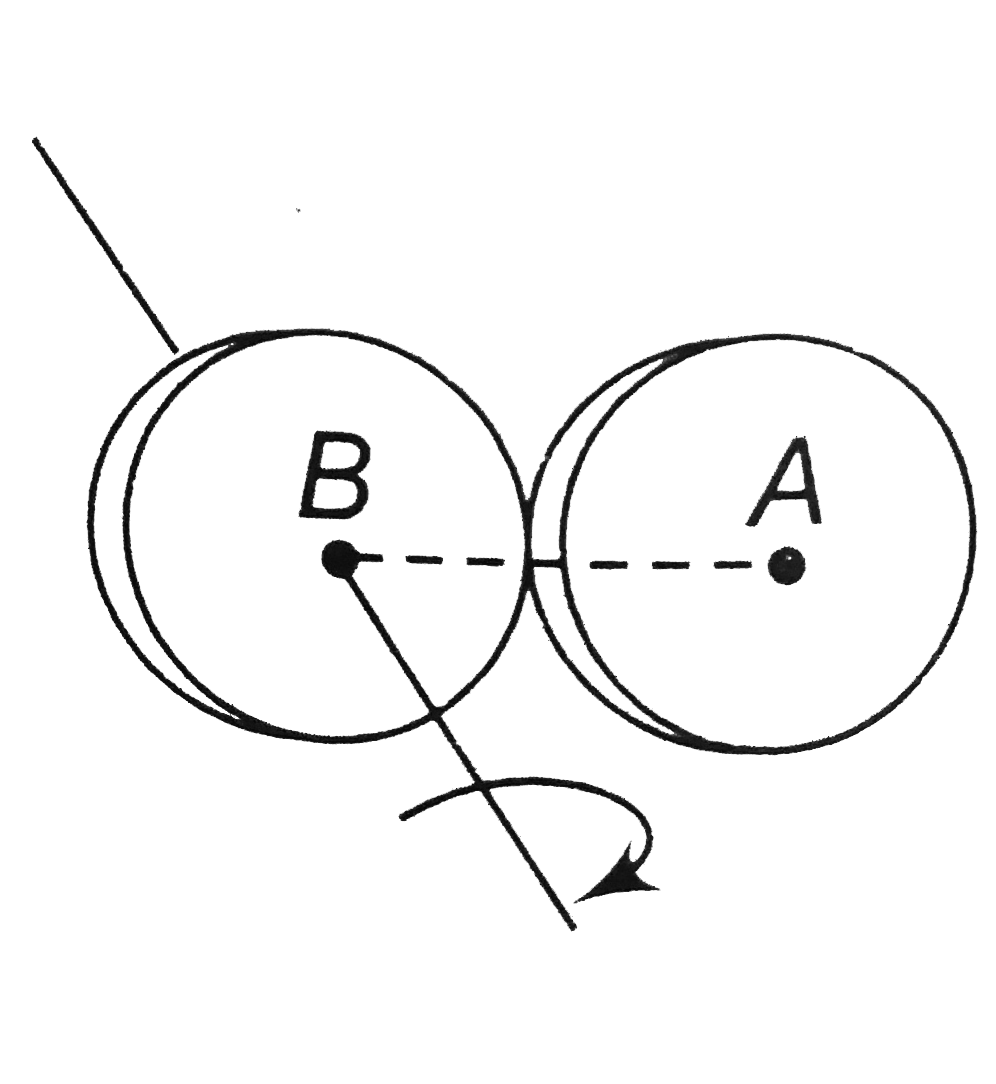
One end of a metal rod of length L and mass M is pivoted to a fixed support and to its free end, a thin disc of mass m and radius r (L) is attached at its centre. In one case, the disc is attached to the rod in such a way that it is not free to rotate about its centre and in another case, teh disc is free to rotate about its centre. When the rod-disc system is displaced slightly from its equilibrium position and released. it peforms S.H.M. in vertical plane. Compare the restoring torque acting on the system and angular frequency in both the cases.

Explanation

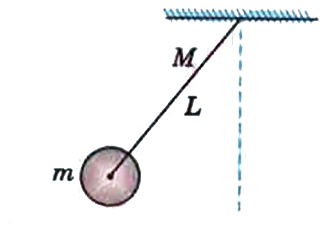
We Know that, torque `tau = Ialpha`
where I is the moment of inertia of the system and `alpha` is the angular acceleration
for case I : When the disc is not free to rotate about its centre
`tau_(1) = I_(1)alpha_(1)`
or `Mg((L)/(2)sin theta) + mg(L sin theta)`
` = ((ML^(2))/(3) + (mR^(2))/(2) + mL^(2))alpha_(1)" "...(i)`

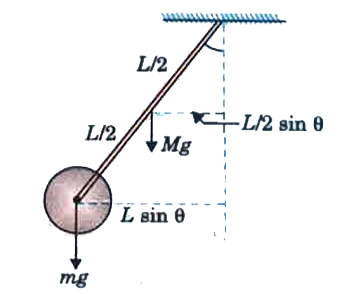
for case : II when the rod is free to rotate
or `Mg((L)/(2)sin theta) + mg(L sin theta) = ((ML^(2))/(3) + mL^(2)) alpha_(2) " "...(ii)`
Comparing (i) and (ii), we get
`tau_(1) = tau_(2) and I_(1) gt I_(2)`. so
`alpha_(1) lt alpha_(2)`
`therefore omega_(A) lt omega_(B)`