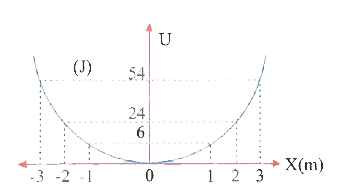
Figure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
A
−12N
B
−24N
C
−16N
D
−8N
Video Solution
Text Solution
The correct Answer is:(2)
The given graph is according to the equation x2=4ay
Substituting 4=(4a)(24)⇒=16
∴x2=16U⇒U=6x2
F=−dUdx=−12x
=−24N
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Figure given below shows the variation of potential energy function U(x), corresponding to one dimensional force field. The point on the graph representing the position of most stable equilibrium is :
(##NAR_NEET_PHY_XI_P2_C06_E09_112_Q01.png" width="80%">AABBCCDDThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,
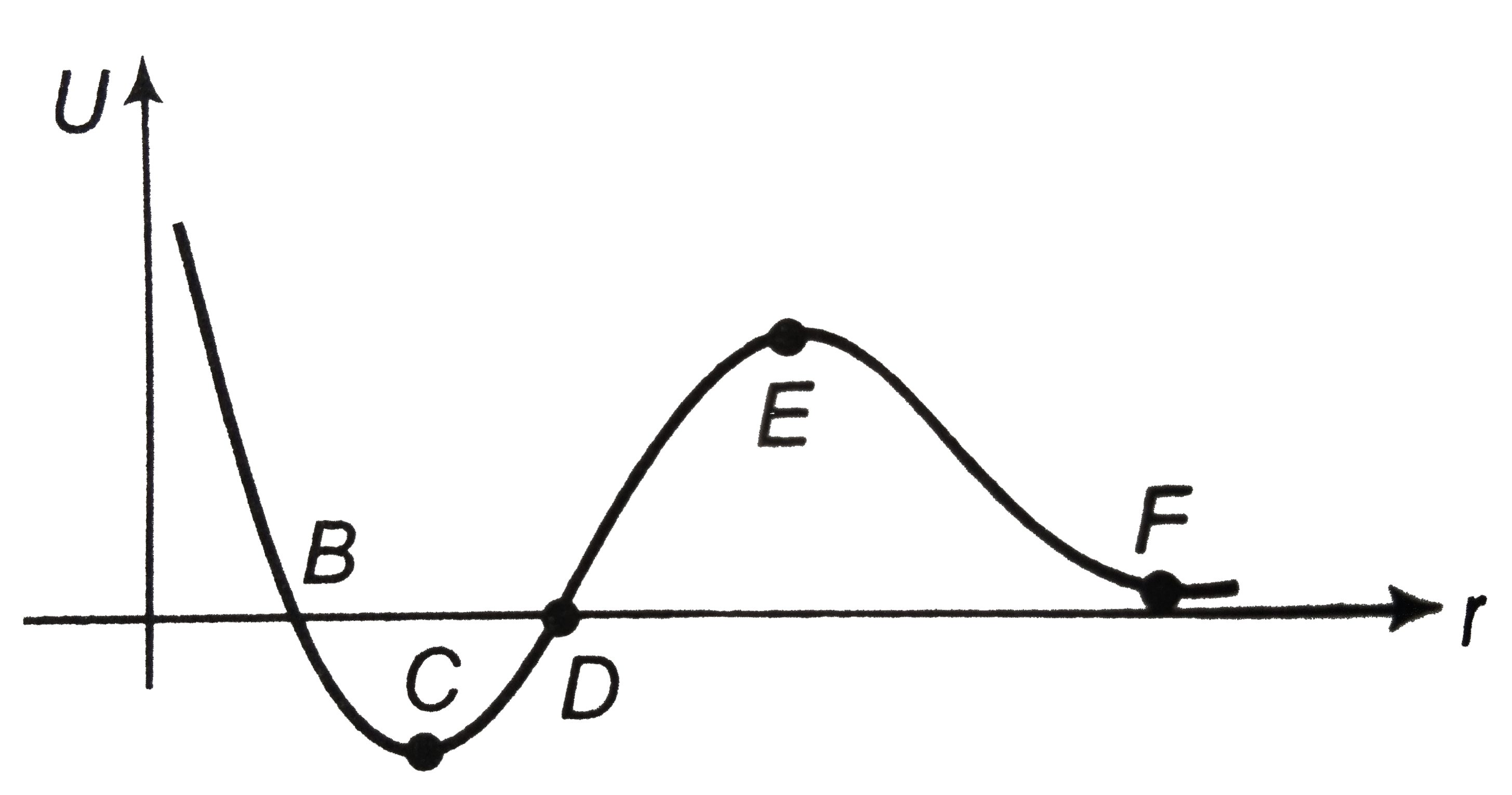 AB and D are equilibrium pointsBC is a point of stable equilibriumCThe force of stable equilibrium between the two particles is attracive between points C and D and repulsive between D and E .DThe force of interaction between particles is repulsive between points E and F.
AB and D are equilibrium pointsBC is a point of stable equilibriumCThe force of stable equilibrium between the two particles is attracive between points C and D and repulsive between D and E .DThe force of interaction between particles is repulsive between points E and F.Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha Emech=8 J, the incorrect statement for this system is :
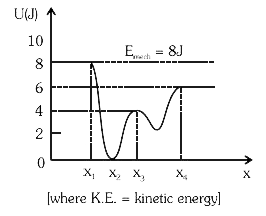 Aat x>x4, K.E. is constant throughout the region.Bat x<x1 K.E. is smallest and the particle is moving at the slowest speed.Cat x=x2 , K.E is greatest and the particle is moving at the fastest speed.Dat x=x3, K.E. = 4 J
Aat x>x4, K.E. is constant throughout the region.Bat x<x1 K.E. is smallest and the particle is moving at the slowest speed.Cat x=x2 , K.E is greatest and the particle is moving at the fastest speed.Dat x=x3, K.E. = 4 J
A potential energy function for a two-dimensional force is the form U=3x2y−7x. Find the force that acts at the point (x,y).
View SolutionThe potential energy function of a particle in a region of space is given as U=(2xy+yz) J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
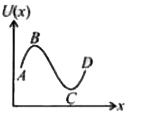
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at

View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
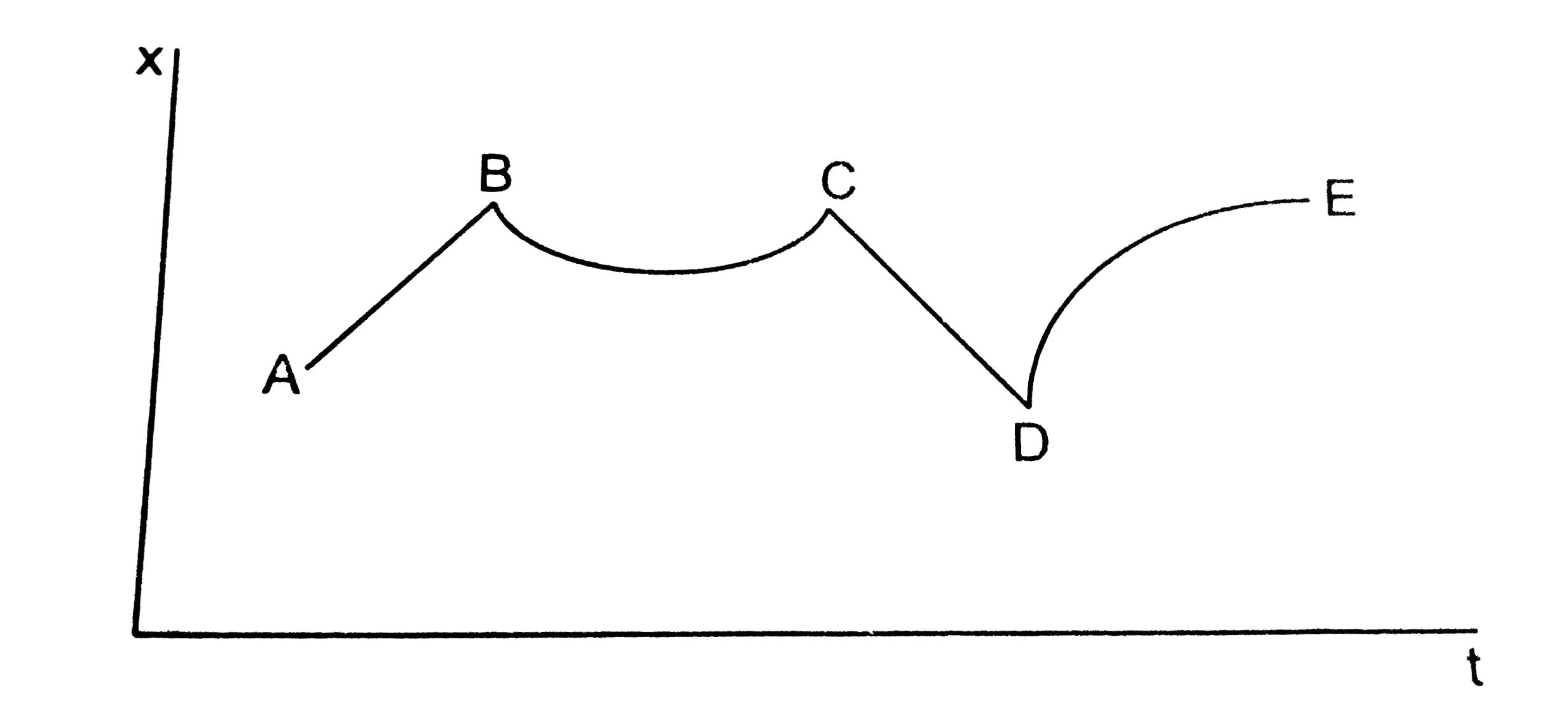
View Solution

