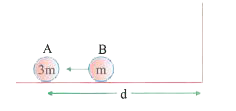
A ball A of mass 3m is placed at a distance d from the wall on a smooth horizontal surface Another ball B of mass m moving with velocity u collides with ball A. The coefficient of restitution between the balls and the wall and between the balls is e
(a) the velocity of ball B after collision is u(3e−1)4.
(b) the velocity of ball B after collision is u(2e−1)4.
( c) after collision, ball A will have away by distance d(2e−1)(2e−1) during the time ball B returns back to wall.
(d) after collision, ball A will move away by distance d(e−1)(3e−1) during the time ball B returns back to wall.
a,d
a, c
b,d
c,d
The correct Answer is:(1)
vA=(1+e)m1u1m1+m2,vB=−(m1−em2)u1m1+m2
tB=dvB,dA=vtA_(B)
Topper's Solved these Questions
Similar Questions
A ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View Solution
Knowledge Check
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
Av1=(1−e)u2,v2=(1+e)u2Bv1=(1+e)u2,v2=(1−e)u2Cv1=u2,v2=−u2Dv1=(1+e)u,v2=(1−e)uA ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?
A1−e1+eBe−1e+1C1+e1−eD2+ee−1A ball of mass moving with a velocity u collides head on with a ball B of mass m at rest. If the coefficient of restitution is e. the ratio of final velocity of B to the initial velocity of A is
A1−e1+eB1+e1−eC1+e2D1−e2
A ball P is moving with a certain velocity , collides head-on with another ball Q of same mass is rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionA ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionThe first ball of mass m moving with a velocity u collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, the ratio of final velocity of the second ball to the initial velocity of the first ball is
View Solution

