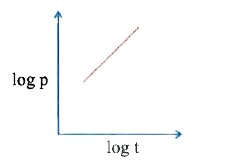
A particles moves along a circle of a fixed radius with a variable acceleration given by $a_{n} = k t^{n},$ where k is a constant and t time. If the power 'P' delivered by all forces acting on it be plotted against time 't' on a log-log scale, the slope of the straight line obtained is 2 as shown in Figure below. The value of n is:

A

1

B

2

C

3

D

$- 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(3)$

$a_{n} = k t^{n} \Rightarrow \frac{v_{n}^{2}}{r} = k t^{n} \Rightarrow v_{n}^{2} = k r t^{n}$
$p o w e r, P = \frac{(\frac{1}{2} m v_{n}^{2})}{t}$
$P = \frac{\frac{1}{2} m k r t^{n}}{t} \Rightarrow P = (\frac{1}{2} m k r) t^{n - 1}$
$∴ P = k_{1} t^{n - 1}$ where $k_{1}$ be a constant Applying log, $log P = (n - 1) log t + {log k}_{1}$
As slope = (n -1) = 2
$\Rightarrow n = 3$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as $a_{n} = k t^{2} .$ where k is a constant.
Power developed by total at time t is
A $\frac{m k R T}{3}$
B $2 m k R T$
C $\frac{m k R T}{2}$
DmkRT
Question 2 - Select One
A particle of mass m moves along a circular path of radius r with a centripetal acceleration $a_{n}$ changing with time t as $a_{n} = k t^{2}$ , where k is a positive constant. The average power developed by all the forces acting on the particle during the first $t_{0}$ seconds is
A(a) $m k r t_{0}$
B(b) $\frac{m k r t_{0}^{2}}{2}$
C(c) $\frac{m k r t_{0}}{2}$
D(d) $\frac{m k r t_{0}}{4}$
Question 3 - Select One
A particle of mass m impves along a horzontal circle of radius R such that normal acceleration of particle varies with time as $a_{n} = k t^{2} .$ where k is a constant.
Tangential force on particle at t s is
A $2 m \sqrt{k} R$
B $m \sqrt{k} R$
C $\frac{m}{2} \sqrt{k R}$
D $m \sqrt{\frac{k R}{2}}$

NARAYNA-WORK , ENERGY & POWER -EXERCISE IV

Home
Ask Doubt
Profile