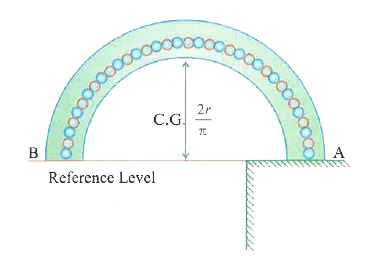
A heavy flexible uniform chain of length πr and mass λπr lies in a smooth semicircular tube AB of radius 'r'. Assuming a slight disturbane to start the chain in motion, find the velocity v with which it will emerge from the end of the tube?
√2π+π2
√2rg(2π+π2)
√2rg(1π+π)
√rf(π+2π)
The correct Answer is:(3)
Centre of gravity of a semicircular arc is at a distance 2rπ from the centre.
Initial potential energy Ui=(λπr)g(2rπ)
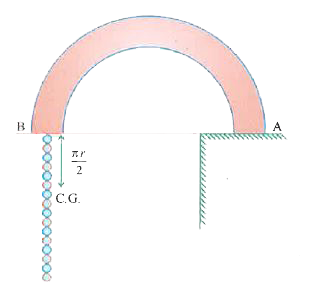
Final potential energy Uf=(λπr)g(−πr2)
When the chain is completely slipped off the tube, all the links of the chain have the same velocity v. Kinetic energy of chain
k=12mv2=12(λπr)v2
From conservation of energy,
λπrg(2ππ)=(λπr)g(−πr2)+12(λπr)v2
On solving we get, v=√2rg(2π+π2)
Topper's Solved these Questions
Similar Questions
A uniform chain of length l and mass m lies on a smooth table. A very small part of this chain hangs from the table. It begins to fall under the weight of hanging part. Find the velocity of chain when the length of hanging part becomes y.
View SolutionA chain AB of length equal to the quarter of a circle of radius R is placed on a smooth hemisphere as shown in figure -3.66. When it is released, it starts falling. Find the velocity of the chain when it falls of the end B from the hemisphere.

View Solution
Knowledge Check
A uniform chain of length of length πr lies inside a smooth semicircular tube (AB) of radius f. Assuming a slight disturbance to start the chain in motion, the velocity it will emerge from the end (B) of the tube will be
 A√gr(1+29π)B√2gr(2π+π2π)C√gr(π+2)D√πgr
A√gr(1+29π)B√2gr(2π+π2π)C√gr(π+2)D√πgrA smooth semicircular tube AB of radius r is fixed in a vertical plane and contains a heavy flexible chain of length πr and weight Wπr as shown. Assuming a slight disturbance to start the chain in motion, the velocity v with it will emerge from the open end B of the tube is:
 A4grπB2grπC√2gr(2π+π)D√2gr(2π+π2)
A4grπB2grπC√2gr(2π+π)D√2gr(2π+π2)
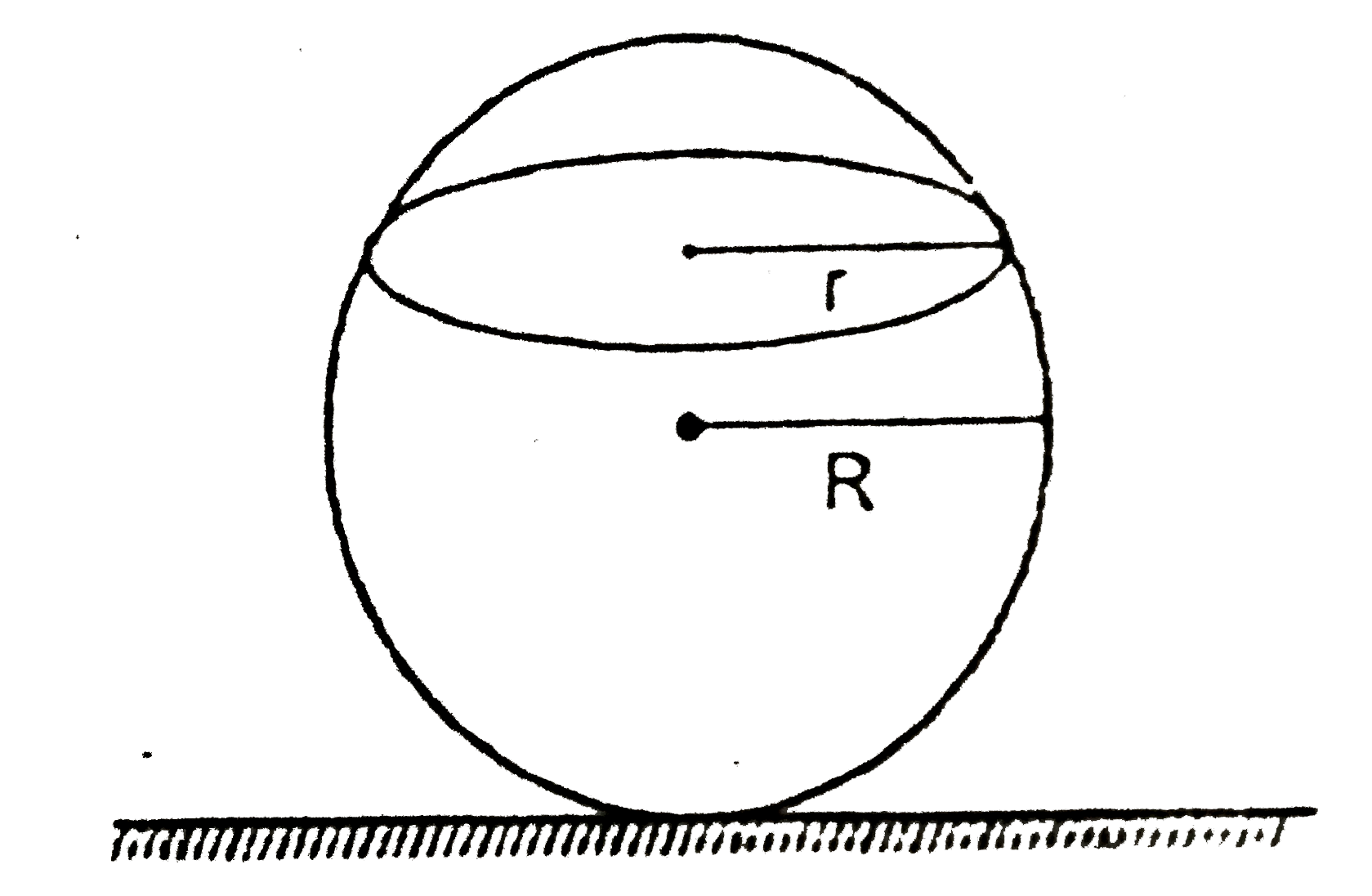
A uniform circular chain of radius r and mass m rests over a sphere of radius R as shown in figure. Friction is absent everywhere and system is in equilibrium . Find the tension in the chain.
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionThe flexible bicycle type chain of length πr2 and mass per unit length ρ is released from rest with θ=0∘ In the smooth circular channel and falls through the hole in the supporting surface, Determine the velocity v of the chain as the last link leaves the slot.
 .
.
View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA chain of mass m and radius R placed on a smooth table is revolving with a speed v about a vertical axis coinciding with the symmetry axis of the chain. Find the tension in the chain.
View SolutionA homogeneous chain of length 2l and mass M lies on an absolutely smooth table. A small part of the chain hangs from the table. At the initial moment, the part of the chain lying on the table is held and released, after which the chain begins to slide off the table under the weight of the hanging end. Find the velocity of the chain when the length of the hanging part is equal to x(x<I). Also calculate the acceleration and the force with which it acts on the edge of the table.
View Solution

