A chain AB of length equal to the quarter of a circle of radius R is placed on a smooth hemisphere as shown in figure -3.66. When it is released, it starts falling. Find the velocity of the chain when it falls of the end B from the hemisphere.

The correct Answer is:[[√gR(x2+4π)]
Step by step video, text & image solution for A chain AB of length equal to the quarter of a circle of radius R is placed on a smooth hemisphere as shown in figure -3.66. When it is released, it starts falling. Find the velocity of the chain when it falls of the end B from the hemisphere. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question
31 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
Find out the flux through the curved surface of a hemisphere of radius R if it is placed in a uniform electric field E as shown in figure
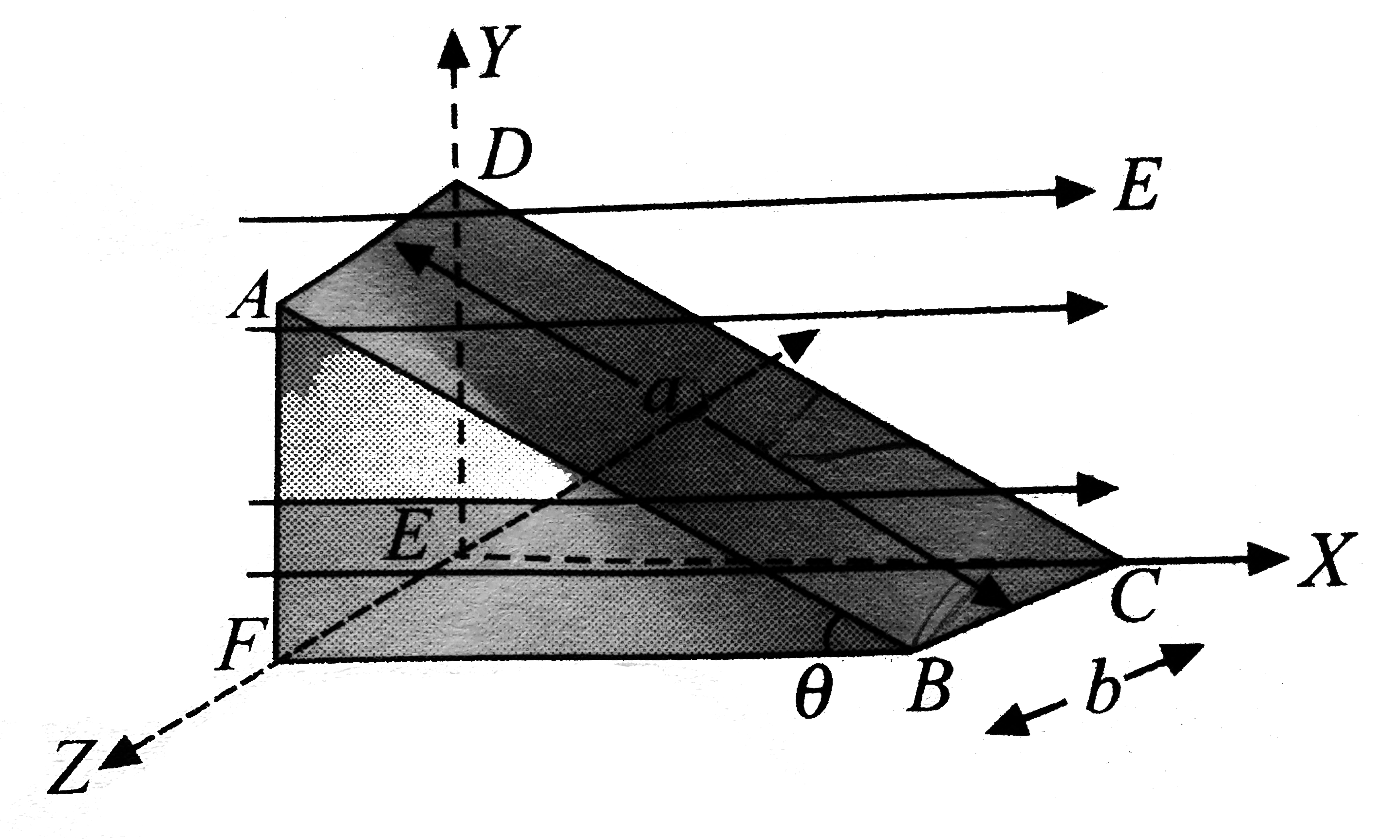
View SolutionTwo smooth wedges of equal mass m are placed as shown in figure. All surfaces are smooth. Find the velocities of A & B when A hits the ground.
View Solution
Knowledge Check
A smooth chain (AB) of mass (m) rests against a surface in the form of a quarter of circle of radius R. If it is released from rest, the form of a quarter of a circle of radius R. If it is releaded from, the velocity of the chain after it comes over the horizontal part of the surface is .
 A(a) √2gRB(b) √gRC(c) √2gR(1−2π)D(d) √2gR(2−π)
A(a) √2gRB(b) √gRC(c) √2gR(1−2π)D(d) √2gR(2−π)A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
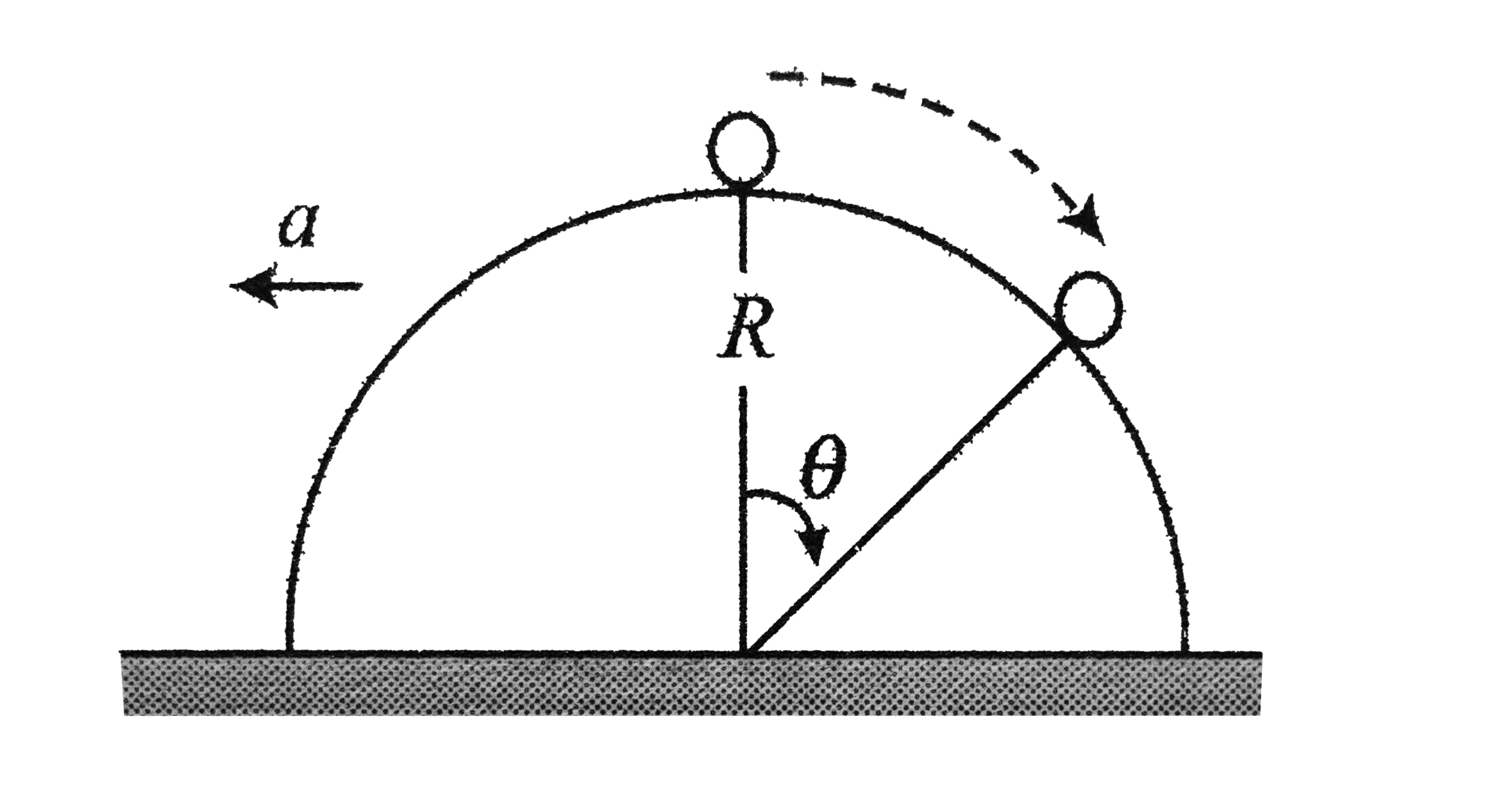 A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]A rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
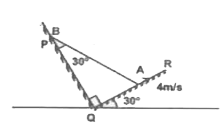 A8m/sB2√3m/sC4√3m/sD4√3m/s
A8m/sB2√3m/sC4√3m/sD4√3m/s
A uniform chain of mass m and length l is placed on a smooth table so that one−third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?

View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionA chain of length L and mass m is placed upon a smooth surface. The length of BA is (L−b). Calculate the velocity of the chain when its and reaches B

View Solution
