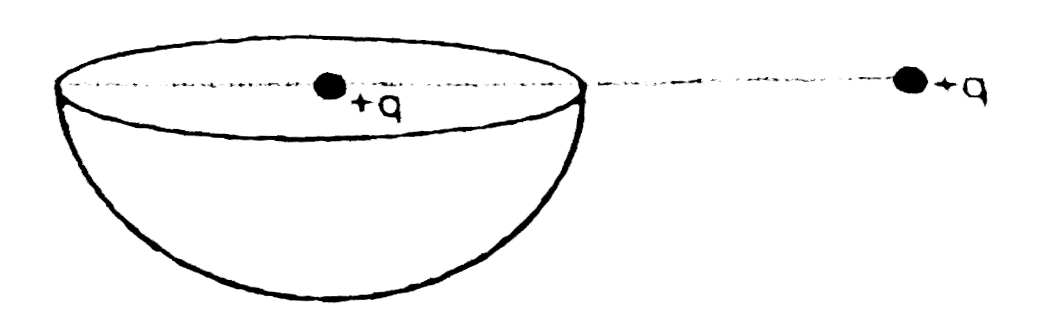
Find out the flux through the curved surface of a hemisphere of radius R if it is placed in a uniform electric field E as shown in figure
The number of electric line passing through the base of the hamisphere is the same as that of the lines passing through the hemisphere. The flux associated with the base of the hemisphere is (negative as it is the incoming flux). Hence, the same amount of flux wil be associated with curved surface, but the sigh of the flux will be positive as it is as outgoing flux. Hence,
.
 .
.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Example
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
Knowledge Check
A hemisphere (radius R) is placed in electric field as shown in fig. Total outgoing flux is -
 AπR2EB2πR2EC4πR2ED(πR2E)/2
AπR2EB2πR2EC4πR2ED(πR2E)/2A hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
Aπr2EB2πrE2C4πr2ED4πrE2The electric flux through a hemispherical surface of radius R placed in a uniform electric field E parallel to the axis of the circular plane is
A(2πR)EB(πR2)EC(43πR3)ED(23πR3)E
Find flux through the hemispherical surface

View SolutionIf a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is E B
View SolutionA solid conducting sphere of radius R is placed in a uniform electric field E as showo in figure. Due to electric field non uniform surface charges are induced on the surface of the sphere. Consider a point A on the surface of sphere at a polar angle θ from the direction of electric field as shown in figure. Find the surface density of induced charges at point A in terms of electric field and polar angle θ : lt brgt

View SolutionThe length and radius of a cylinder are L and R respectively. The total flux for the surface of the cylinder, when it is placed in a uniform electric field E parallel to the axis of the cylinder is
View SolutionCalculate the total electric flux through the paraboloidal surface due to a uniform electric field of magnitude E0 in the direction shown in figure.
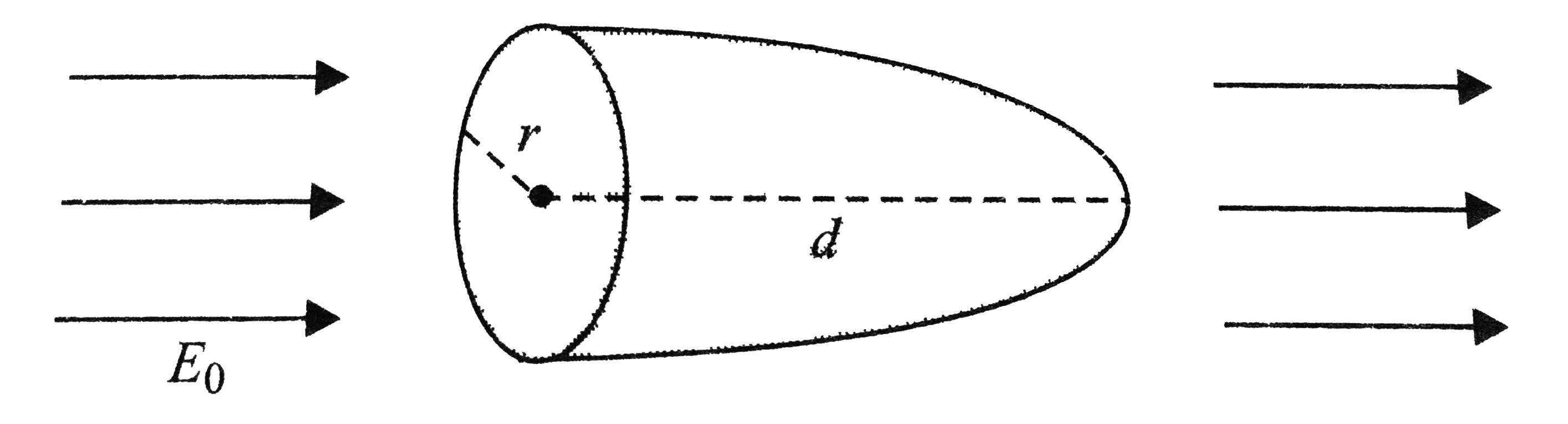
View Solution