Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
L3
3L4
4L3
5L3
The correct Answer is:(4)
v=√g(3h−r) Where h is maximum height at which the tension in the string is zero.
Topper's Solved these Questions
Similar Questions
The bob of a simple pendulum of length 1m hangs at rest. It is suddenly projected horizontally with velocity 10ms−1. Calculate the velocity of the bob and tension of the string when it is horizontal. The mass of the bob is 12kg.
[Hint : See worked out example 4]
View SolutionBob of a simple pendulum of length L is projected horizontally with a speed of u=√4gh, , from the lowest position. Find the distance of the bob from vertical line AB, at the moment its tangential acceleration becomes zero.
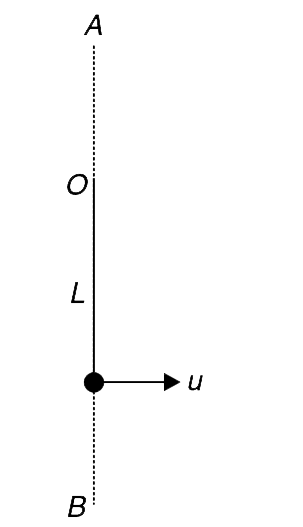
View Solution
Knowledge Check
The bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
AmgB2 mgC3 mgD6 mgThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
AmgB3 mgC2 mgD6 mgA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
A30∘B90∘C120∘D150∘
The bob of a simple pendulum of length l is given a sharp hit to impart it a horizontal speed of √3gl . When it was at its lowermost position. Find
angle α shown of the string from upside of vertical and speed of the particle when the string becomes slack.

View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionA simple pendulum has a bob of mass m and string of length R. The bob is projected from lowest position giving it a horizontal velocity just enough for it to complete the vertical circle. Let the angular displacement of the pendulum from its initial vertical position be represented by θ. Plot the variation of kinetic energy (kE) of the bob and the tension (T) in the string with θ. Plot the graph for one complete rotation of the pendulum.
View SolutionIf the inertial mass m1 of the bob of a simple pendulum of length 'l' is not equal to the gravitationalmassmg, then its period is
View SolutionThe velocity of the bob of a simple pendulum in the mean position is v. If its amplitude is doubled, by keeping the same length, then its velocity in the mean position will be
View Solution
