A potential energy function for a two-dimensional force is the form U=3x2y−7x. Find the force that acts at the point (x,y).
Fx=−∂U∂x=−∂(3x3y−7x)∂x=−(9x2y−7)=7−9x2y
Fy=−∂U∂y=−∂(3x3y−7x)∂y=−(3x3−0)=−3x3
Thus, the force acting at point (x,y) is
→F=Fxˆi+Fyˆj=(7−9x2y)ˆi−3x3ˆj
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.3
Explore 26 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.4
Explore 16 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
[" 5.The potential energy function for a two dimensional force is "],[U=+2x^(3)-4x^(2)y+6y^(2)" where "U" is in joules,"x" and "y" are in metres.The force (in "N)],[" acting on particle at "(3m,2m)" is "(Ahat i+Bhat j)" newtons.Find "A+B?]
View SolutionIf the potential energy function of a particle is given by U=−(x2+y2+z2)J, whre x,y and z are in meters. Find the force acting on the particle at point A(1m,3m,5m).
View Solution
Knowledge Check
Figure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
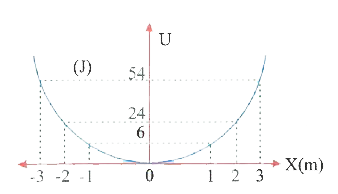 A−12NB−24NC−16ND−8N
A−12NB−24NC−16ND−8NThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
A−3kB+3kCkDNone of theseThe potnetial energy for a force field →F is given by U(x,y)=cos(x+y). The force acting on a particle at the position given by coordinates (0,π/4) is
A−1√2(ˆi+ˆj)B1√2(ˆi+ˆj)C(12ˆi+√32ˆj)D(12ˆi−√32ˆj)
The potential energy function of a particle in a region of space is given as U=(2xy+yz) J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy function of a particle due to some gravitational field is given by U=6x+4y. The mass of the particle is 1kg and no other force is acting on the particle. The particle was initially at rest at a point (6,8). Then the time (in sec). after which this particle is going to cross the 'x' axis would be:
View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View SolutionThe potential energy for a force filed →F is given by U(x,y)=cos(x+y). The force acting on a particle at position given by coordinates (0,π/4) is
View Solution

