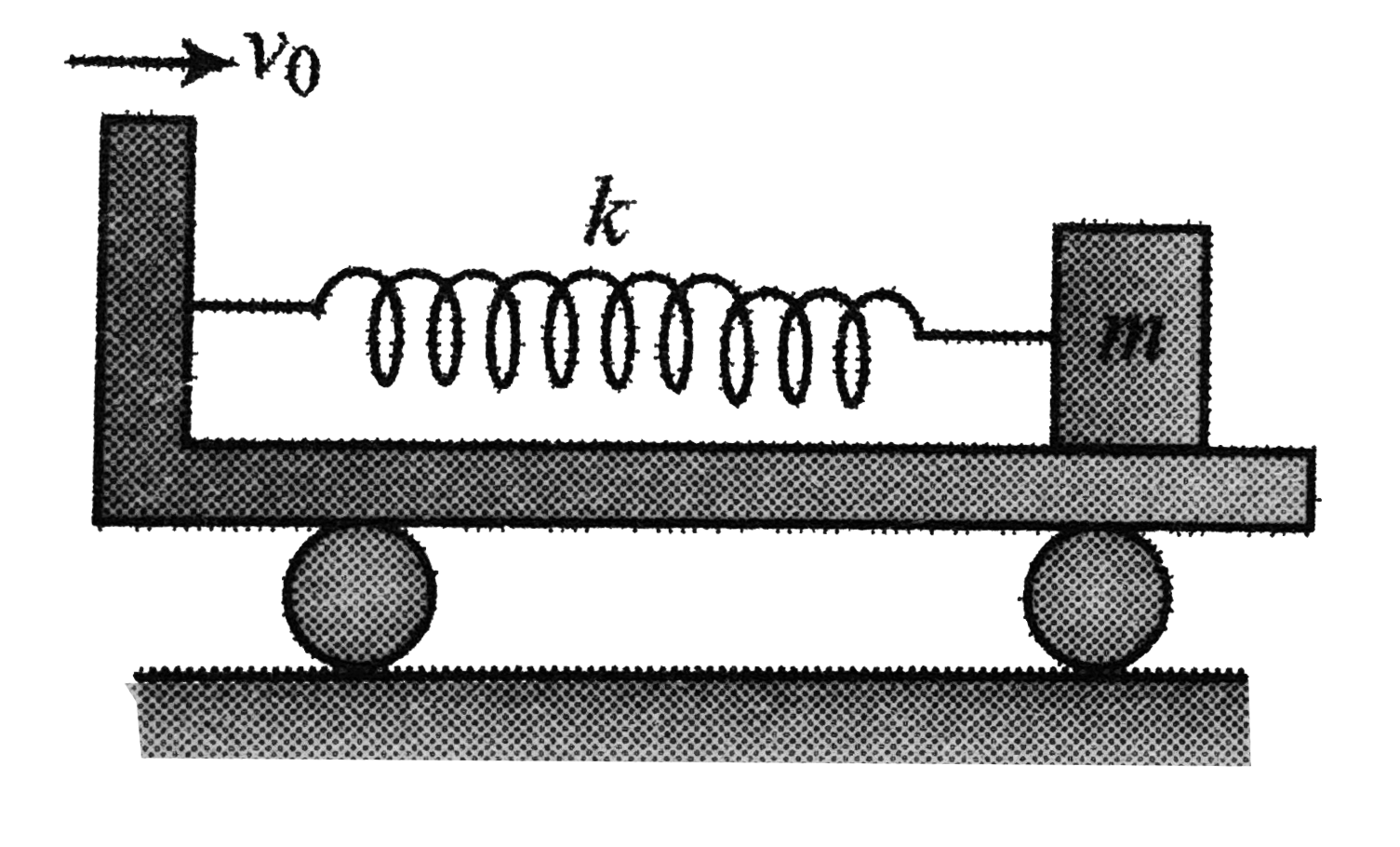
A block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.
As the block moves, spring force Fs=(kx) increases till it nullifies fk(=μmg). In consequence, the block will stop.
ΔK: When the block will stop,
ΔK=−12mv20
Wsp: When the block stops finally, let us assume that the spring is deformed by an amount x.
Then the work done by the spring is
Wsp=−kx22

The work done by friction Wf is given as Wf+Wsp=ΔK.
Substituting ΔK=−12mv20 and Wsp=−kx22, we have
Wf=kx22−12mv20
where x can be calculated by equating the forces acting on the stationary block.
Since the block is at the verge of sliding, we have
kx=μmg
This gives x=μmgk
Now substituting x=μmgk in the above expression of work, we have Wf=μ2m2g22k−12mv20

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
View Solution
Knowledge Check
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
 Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)
Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)A block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
 A12 NB13 NC17 ND16 N
A12 NB13 NC17 ND16 NA block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?
 A0.40B0.50C0.25Dnone of these
A0.40B0.50C0.25Dnone of these
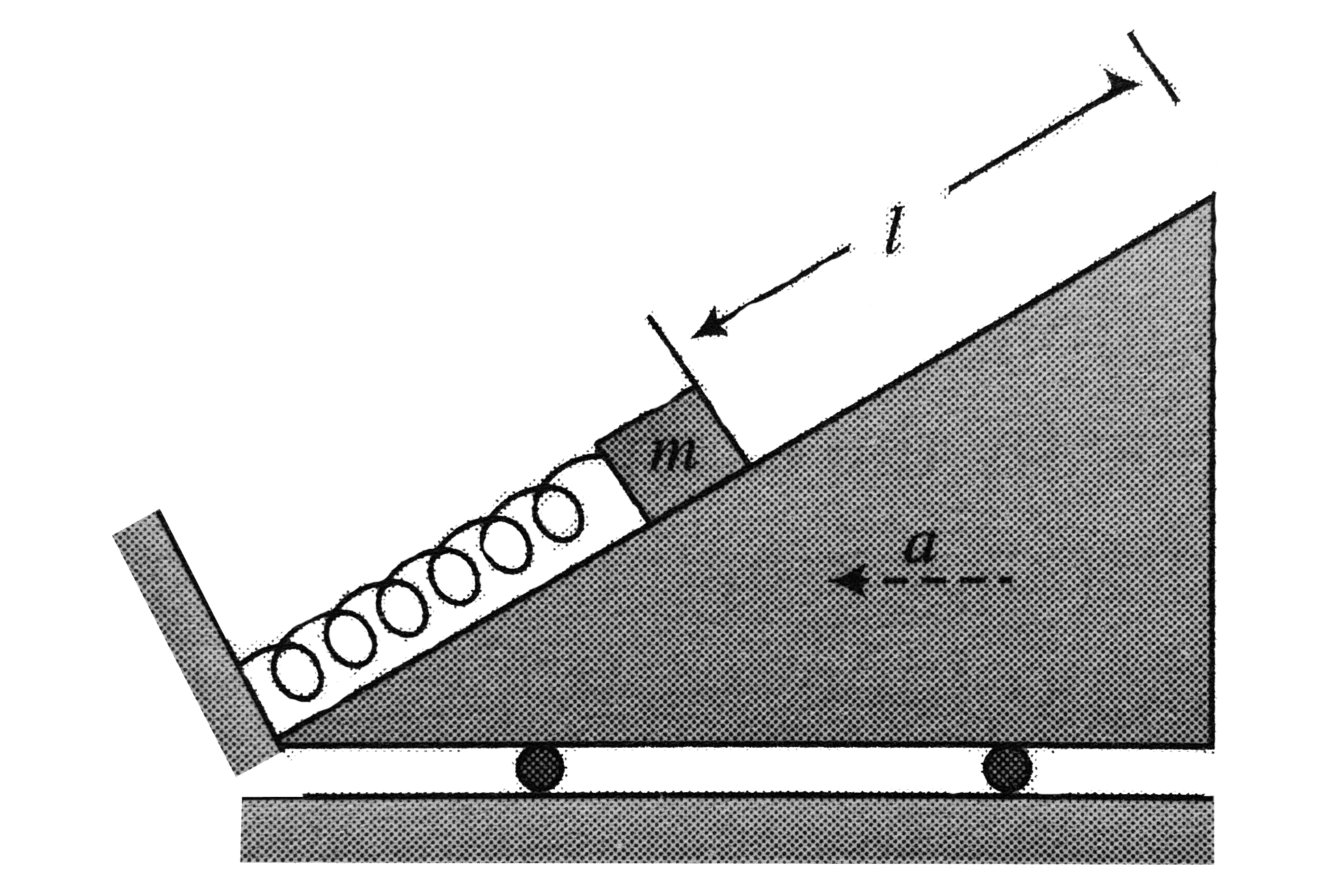
A block of mass m is welded with a light spring of stiffness k. The spring is initially relaxed. When the wedge fitted moves with an acceleration a, as shown in figure. 8.60, the block slides through a maximum distance l relative to the wedge. If the coefficient of kinetic friction between the block and the wedges is μ, find the maximum deformation l of the spirng by using work-energy theorem.
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View SolutionThe block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
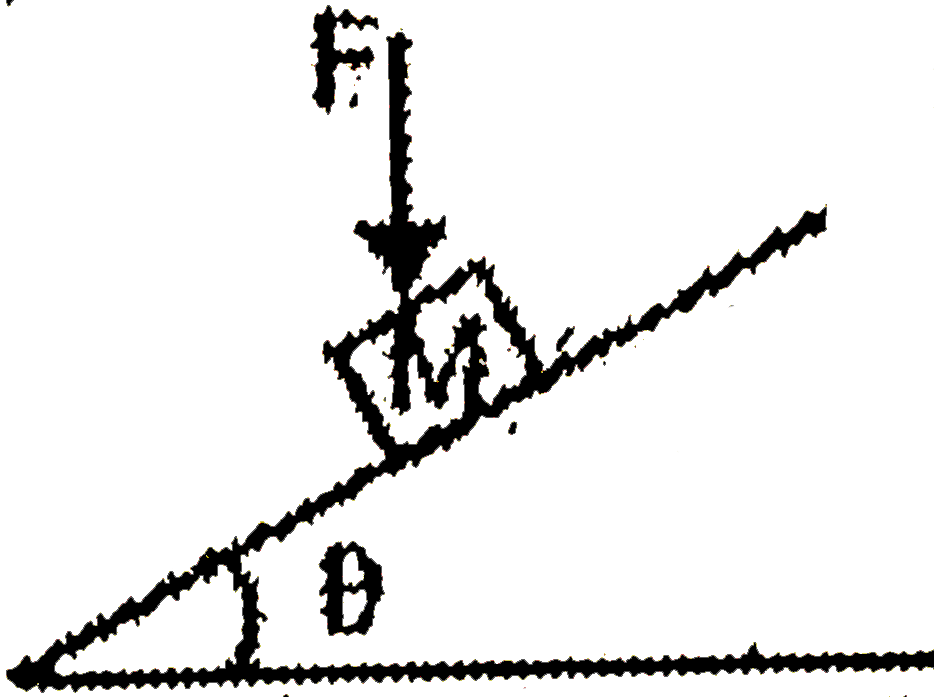
View SolutionA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
View Solution
