A spring block system is placed on a rough horizontal surface having coefficient of friciton μ. The spring is given initial elongation 3μmg/k (where m=mass of block and k=spring constant) and the block is released from rest. For the subsequent motion, find
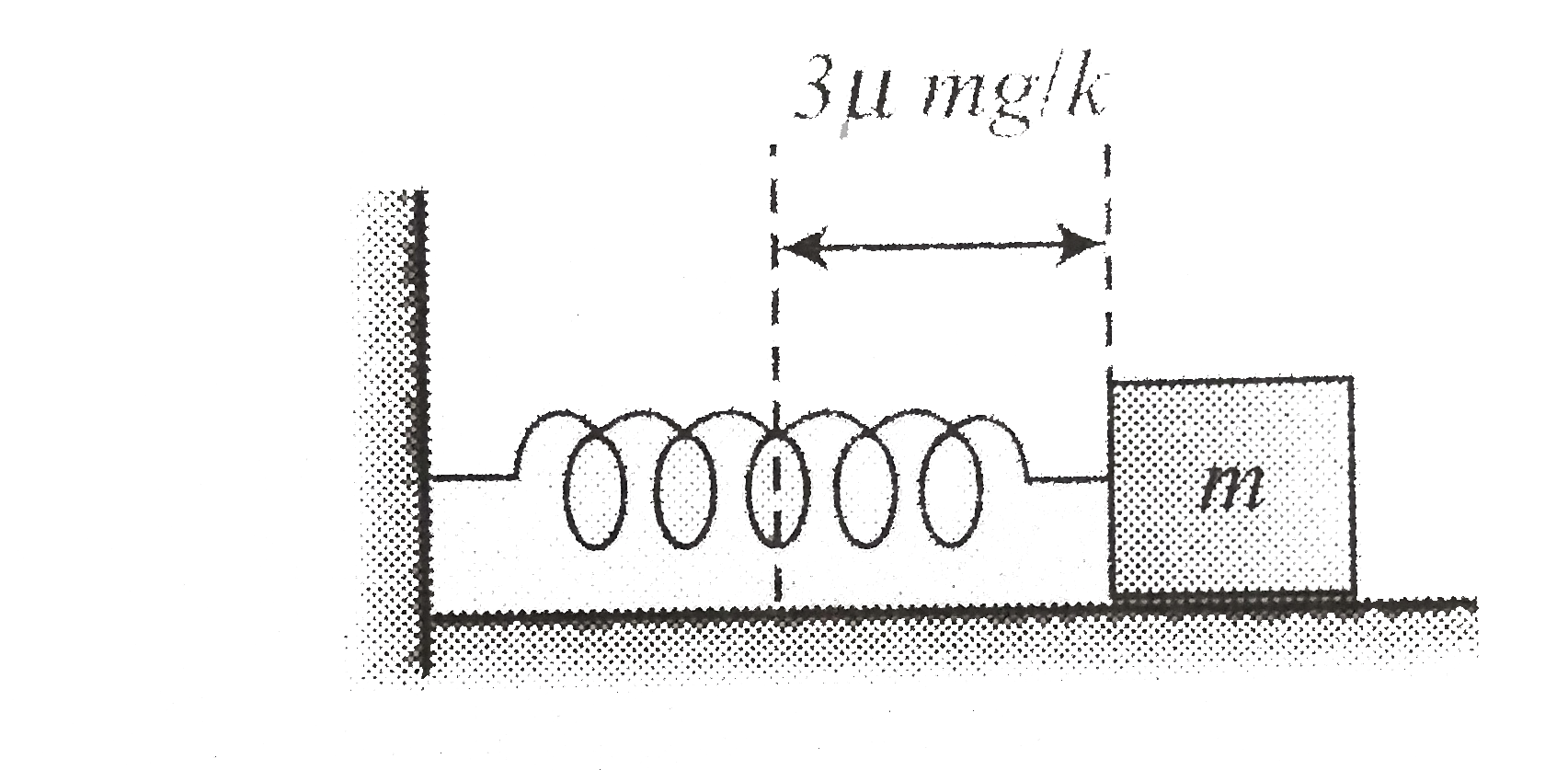
a. Initial acceleration of block
b. Maximum compression in spring
c. Maximum speed of the block
a. From Newton's second law, we get
ma=3μmg−μmg⇒a=2μg
b. From work energy principle
Wspr∈g+Wspr∈g=0
12k(x20−x21)−μmg(x1+x0)=0
x0−x1=2μmgk⇒x1=μmgk
c. Speed will be maximum where net force is zero
μmg=kx
⇒x=μmgk (extension)
Now from work-energy principle, we have
12k(μmgk)2(32−12)−2μmgk(μmg)=12mv2
Solving we get, v=2μg√mk
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.3
Explore 26 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.4
Explore 16 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
A spring block system is placed on a rough horizontal floor. The block is pulled towards right to give spring some elongation and released.
 AThe block may stop before the spring attains its natural lengthBThe block must stop with spring having some comprission.CThe block may stop with spring having some compression.DIt is not possible that the block stops at antural length of the spring.
AThe block may stop before the spring attains its natural lengthBThe block must stop with spring having some comprission.CThe block may stop with spring having some compression.DIt is not possible that the block stops at antural length of the spring.A spring block system is placed on a rough horizontal floor. The block is pulled towards right to gives spring some elongation and released, Then :
 Athe block may stop before the spring attains its natural lengthBthe block must stop with spring having some compressionCthe block may stop with spring having sme compressionDit is not possible that the block stops at mean position
Athe block may stop before the spring attains its natural lengthBthe block must stop with spring having some compressionCthe block may stop with spring having sme compressionDit is not possible that the block stops at mean positionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mg
In the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
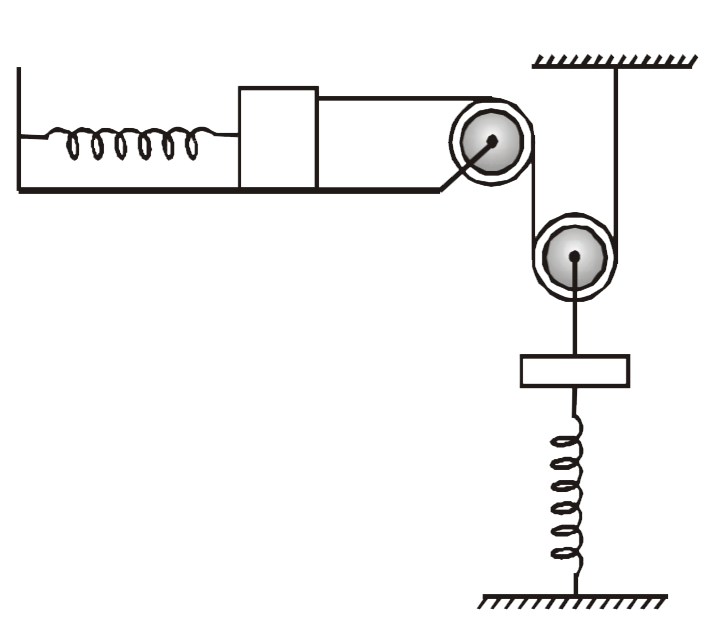
Maximum speed of the block placed horizontally is:
View SolutionA spring block system is placed on a rough horizontal floor. The block is pulled towards right to give spring an eleongation less than 2μmgK but more than μmgK and released.
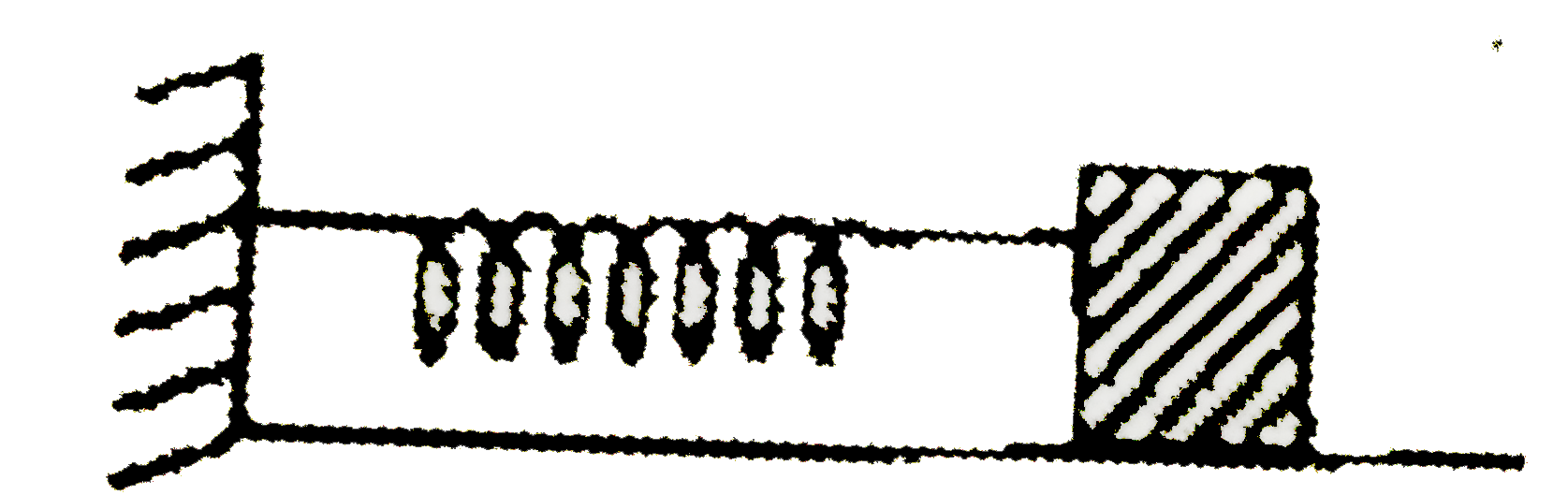
The correct statement is :
View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
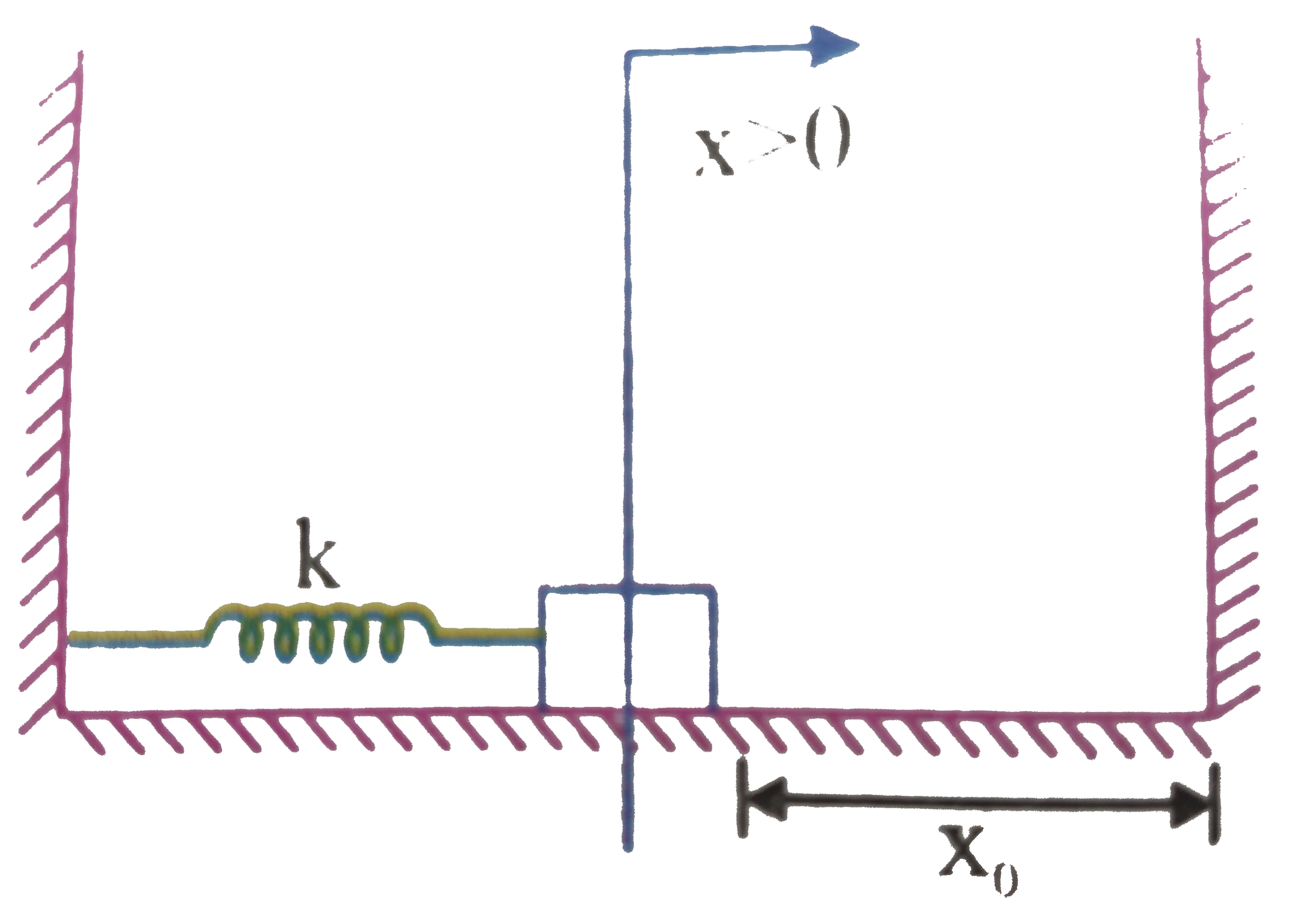
Find the time period of motion of the block:
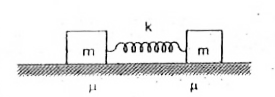
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View Solution

