A small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.
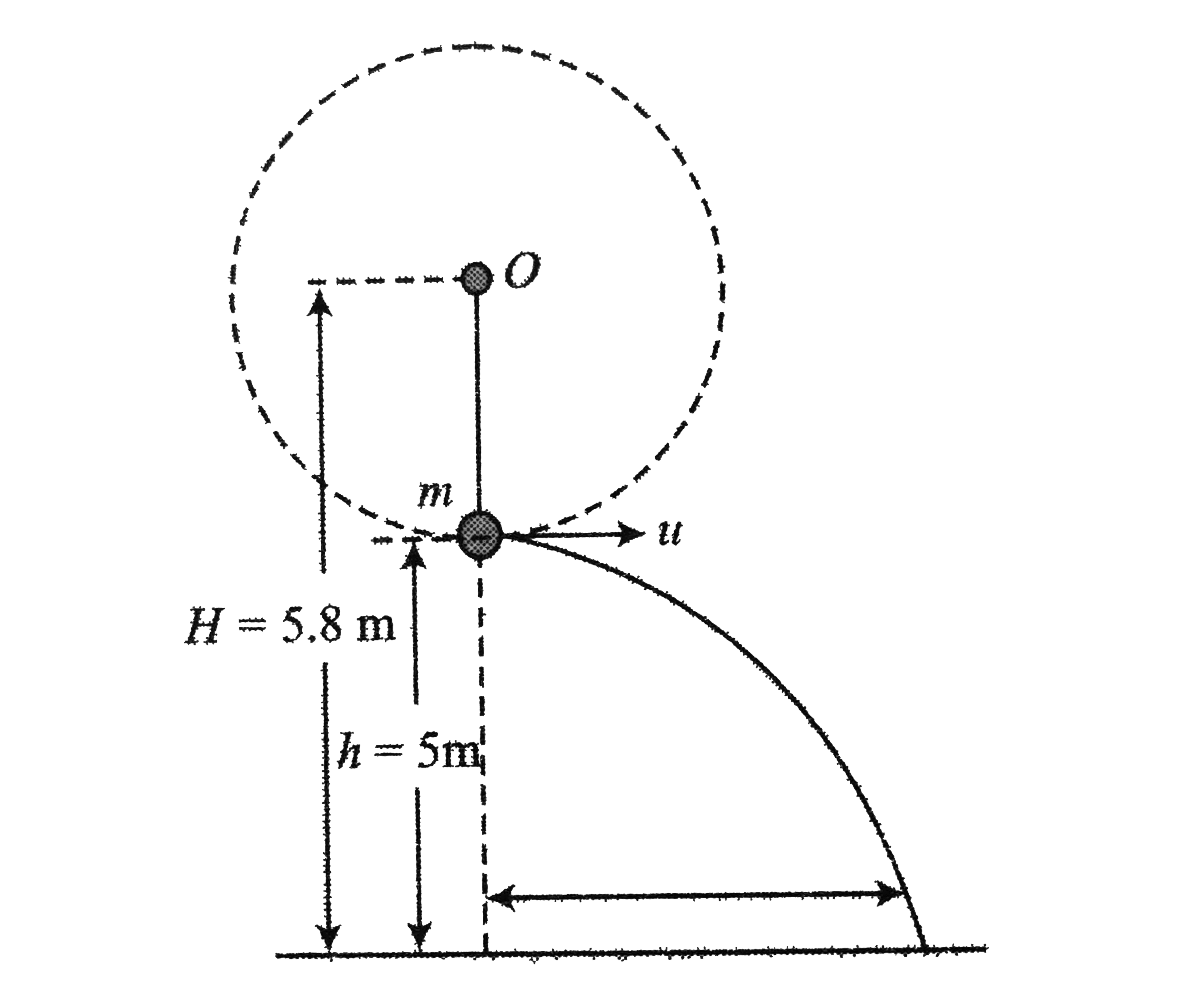
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
(a) Let u and v be the speed of sphere at the bottom and the top positions and m be its mass.
Radius of circle = length of string = r = 0.8 m<br>T_(b) = tension at the bottom or the maximum tension<br>T_(t) = tension at the top or the minimum tension
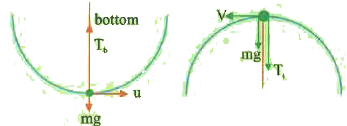
Tb−mg=μ2r
Tt+mg=mv2r
⇒Tb=3Tt
(μ2r+mg)=3(mv2r−mg)
⇒(3v2−u2)=4rg...(i)
Using conservation of energy. Loss in KE from bottom to the top = gain in GPE
12μ2−12(mv)2=mg(2r)
⇒v2=u2−4rg...(ii)
Using (i) and (ii), we get
3(u2−4gr)−u2=4rg ⇒2u2=16rg
⇒u=√8(0.8)10=8ms
(b)After breaking away from the string the sphere moves along a parabolic path, and strikes the ground at G.
Vertical displacement of sphere
(##NARN∃TPHYXIP2C06SLV039_S02.png width=80%><br>T = sqrt(2S_(y))/(g) = sqrt(2xx5)/(10) = 1 sec<br>Sox = u_(x) T = uT = 8 xx 1 = 8 m
The sphere hits the ground after 1 second at a horizontal distance 8m from the fixed end of the string.
Topper's Solved these Questions
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EVALUATE YOURSELF-1
8 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - Evaluate Yourself - 2
8 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV
56 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Integer)
12 Videos
Similar Questions
A small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.

(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionA small bob tied at one end of a thin string of length 1m is describing a vertical circle so that the maximum and minimum tension in the string are in the ratio 5: 1. The velocity of the bob at the height position is ____ m/s. (Take g=10m/s2)
View Solution
Knowledge Check
A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
Am[g+4π2r]Bm[g+π2n2r260]Cm[g+π2n2r900]Dm[g+n2r2]A stone of mass 1 kg tied to a light inextensible string of length L=53m, is whirling in a vertical circle of radius L. If the ratio of the maximum and minimum tension in the string is 4 and g=10m/s2, the speed of stone at the highest point of the circle is
A5m/sB5√3m/sC5√2m/sD10m/sA stone at the end of 1m long string is whirled in a vertical circle at a constant speed of 4ms−1. The tension in the string is 6N when the stone is
A(a) 10ms−1B(b) 5√3ms−1C(c) 10√3ms−1D(d) 20ms−1
A stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
View SolutionIf a bodyy is tied to a string and whirled in vertical circle, then the tension in the string at the highest position is
View SolutionIF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
View SolutionIn the previous problem, tension in the string at the lowest position of the body is
View SolutionA mass of 5 kg is tied to a string of length 1.0 m is rotated in vertical circle with a uniform speed of 4m/s . The tension in the string will be 170 N when the mass is at (g=10m/s2)
View Solution
