A body slides down an inclined surface which ends into a vertical loop of radius R = 40cm.
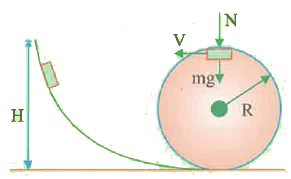
What must be the height H of the inclined surface for the body so that it does not leave contact with the surface even at the uppermost point of the loop? Assume friction to be absent.
Let v be the velocity of the particle of the particle at the highest point. At the highest position the net force on the body is (N+Mg) towards the centre of the path, and which provides the required centripetal force.
Therefore, N+mg=(mv)2R
The body is not detached from the loop if N≥0. In the limiting case, N = 0
That is mg=(mv)2Rorv2=gR
Applying energy conservation at the initial and highest point of the loop, we get.
mgH=mg(2R)+12(mv)2
Using v2=gR, we obtain,
mgH=mg(2R)+12m(gR)or
H=52R=2.5R
Putting R=40cm=0.4m,we get
H=(2.5)(0.4)=1 m.
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EVALUATE YOURSELF-1
Explore 8 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:Evaluate Yourself - 2
Explore 8 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
A ball rolls down an inclined plane from a height and then goes round a vertical circle of radius 1m. What should be the height of the inclined plane so that the ball is able to go round the circle without leaving the track?
View SolutionWhat is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
View Solution
Knowledge Check
A small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
A52RB52(R−r)C2510(R−r)D2710R−17r10A body slides down on a frictionless track which ends in a circular loop of diameter D. The minimum height h in terms of D so that the body may just complete the circular loop, is
 Ah=52DBh=32DCh=54DDh=2D
Ah=52DBh=32DCh=54DDh=2DAn inclined track ends in a circular loop of radius r. From what height on the track a particle should be released so that it completes the loop, assuming there is no friction ?
Ar2B3r2CrD5r2
A particle of mass m is released from a height H on a smooth curved surface which ends into a vertical loop of radius R, as shown. Choose the correct alernative(s) if H=2R.
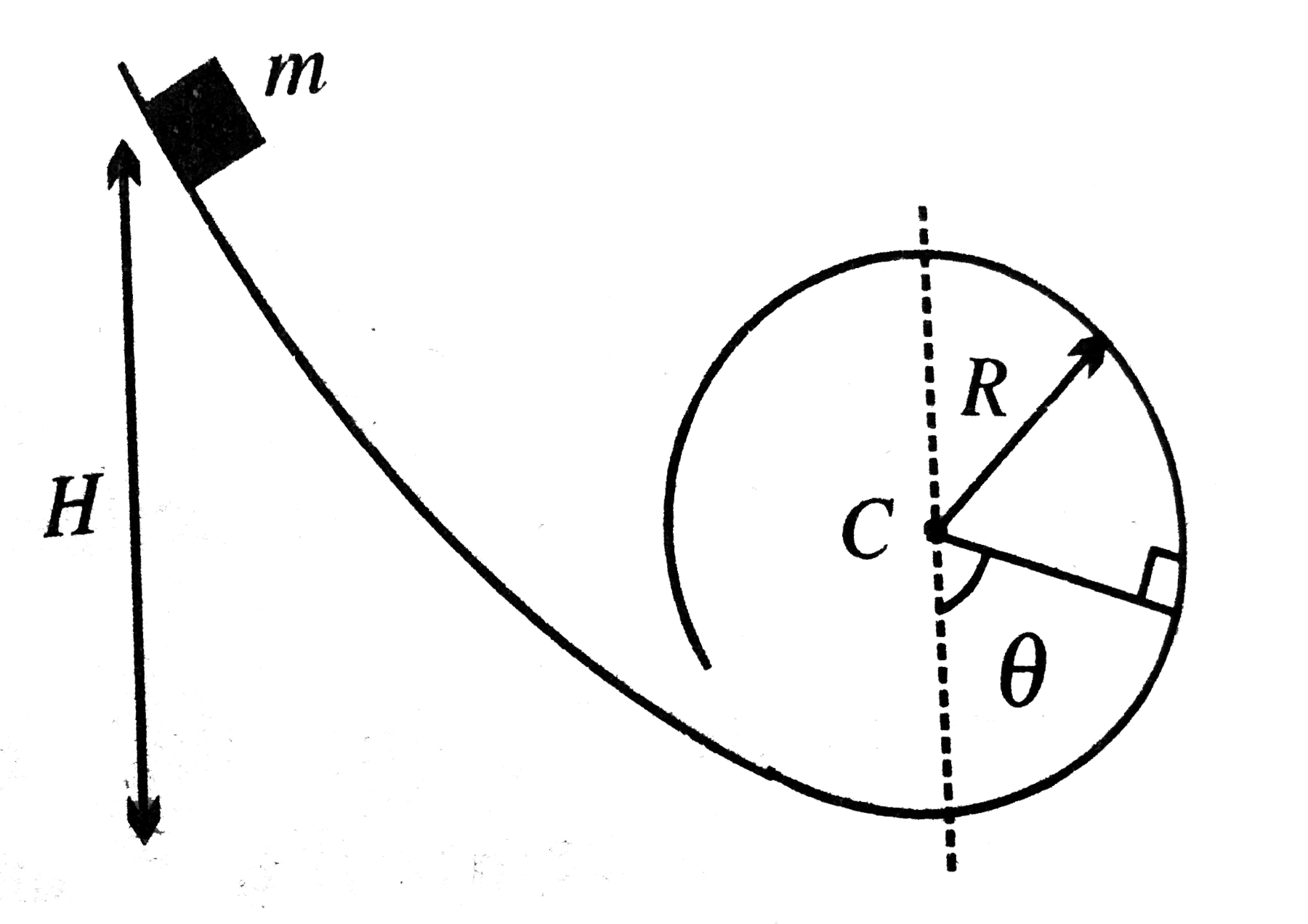
View SolutionA liquid is filled in a spherical container of radius R up to a height h. At this position the liquid surface at the end is also horizontal. The contact angle is

View SolutionThe height at which the weight of the body become 19 th its weight on the surface of earth (radius of earth R)
View SolutionThe coefficient of static friction between contact surfaces of two bodies is 1. The contact surfaces of one body support the other till the inclination is less than
View SolutionThe coefficients of static friction between contact surface of two bodies is 1. The contact surface of one body support the orther till the inclination is less than
View Solution

