The position (x) of a particle of mass 1 kg moving along x-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3 s.
x=12t2⇒v=dxdt=12(2t)=t
∴Att=0,vi=0
At t=3s,vf=3ms−1
According to W-E theorem, W=ΔK=Kf−Ki=12mv2f−12(mv2i
=12×1×32=4.5J
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EVALUATE YOURSELF-1
Explore 8 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:Evaluate Yourself - 2
Explore 8 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
The position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionThe position of a particle of mass 10kg moving along x- axis varies with time as x=2+t2(x is in meter and t is in second).Then work done by net force from t=0 to till body attains velocity of 10m/s is ?
View Solution
Knowledge Check
A particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
A144 JB72 JC108 JD216 JThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The distance travelled by body in time interval t = 0 to t = 3 s is
A5 mB7 mC4 mD3 mThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
A4t+6xB2t−xxC4t+6D2t+3x
The position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
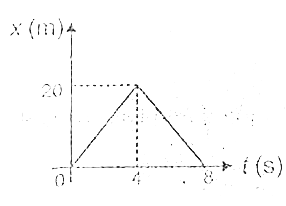
View SolutionThe position x of a particle moving along x - axis at time (t) is given by the equation t=√x+2, where x is in metres and t in seconds. Find the work done by the force in first four seconds
View SolutionThe displacement x of a particle at time t moving under a constant force is t=√x+3, x in metres, t in seconds. Find the work done by the force in the interval from t=0 to t=6 second.
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View Solution