The region between x=oandx=L is filled with uniform, steady magnetic field B0ˆk. A particle of mass m , positive charge q and velocity v0ˆi travels along x−aξs and enters the region of the magnetic field. Neglect gravity throughout the question .
(a) Find the value of L if the particle emerges from the region of magnetic field with its final velocity at angle 30∘ to its initial velocity.
(b) Find the velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends upto 2.1L.
The correct Answer is:(a)mv02qB (b)−v0ˆiπmqB
(a)θ=30∘
sinθ=LR
Here,R=mV0B0q
∴sin30∘=LmV0B0q
or 12=B0qmV0
∴L=mV02B0q
(b)In part (a)
sin30∘=LR
or 12=LR
or L=R/2
Now when L=2.1L or 2.12R
⇒L>R
Therefore, deviation of the particle is θ=180∘ is as shown.
∴→Vf=−V0ˆi−→VB
and tAB=T/2=πmB0q


Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-3 PART-3
Explore 29 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
The region between x=0 and x=L is filled with uniform steady magnetic field B0ˆk. A particle of mass m, positive charge q and velocity v0ˆi travels along x-axis and enters the region of the magnetic field. Neglect the gravity throughout the question.
a. Find the value of l if the particle emerges from the region of magnetic field with its final velocilty at an angel 30∘ to its initial velocity.
b. Find the final velocity of the particle and the time spent by it in the magnetic field, if themagnetic field now extends upto 2.1L.
View SolutionA charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force . The path of the particle is a circle .
View Solution
Knowledge Check
The region between x=0 and x=L is filled with uniform constant magnetic field 25(T)ˆk. A particle of mass m=50g having positive charge q=1C and velocity →V0=50√3ˆi+50ˆjms−1 enters the region of the magnetic field. Neglect gravity throughout the question.
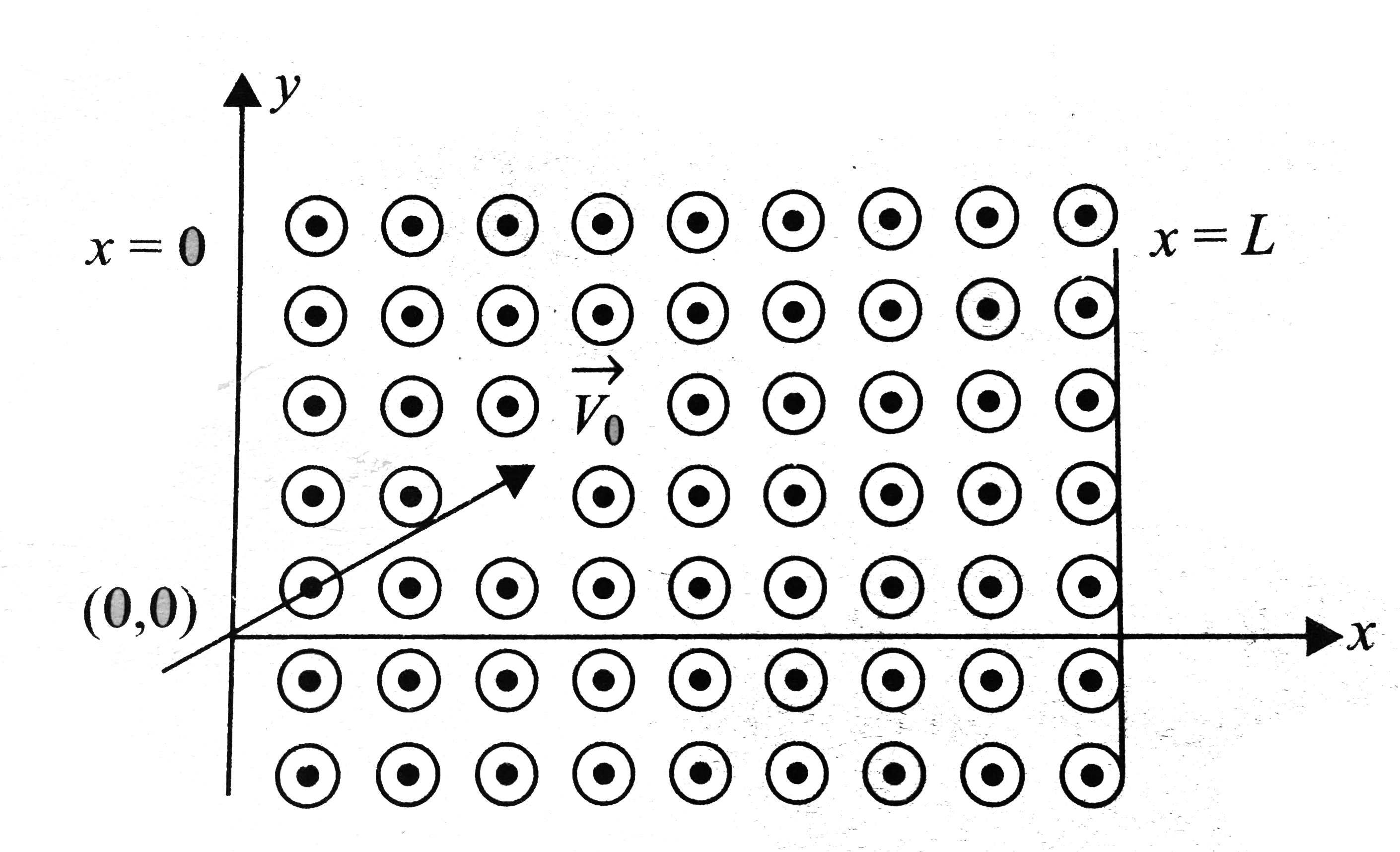
The value of L if the particle emerges from the region of magnetic field with its velocity 100(ms−1)ˆi isA20cmB10cmC30cmDNone of theseThe region between x=0 and x=L is filled with uniform constant magnetic field 25(T)ˆk. A particle of mass m=50g having positive charge q=1C and velocity →V0=50√3ˆi+50ˆjms−1 enters the region of the magnetic field. Neglect gravity throughout the question.
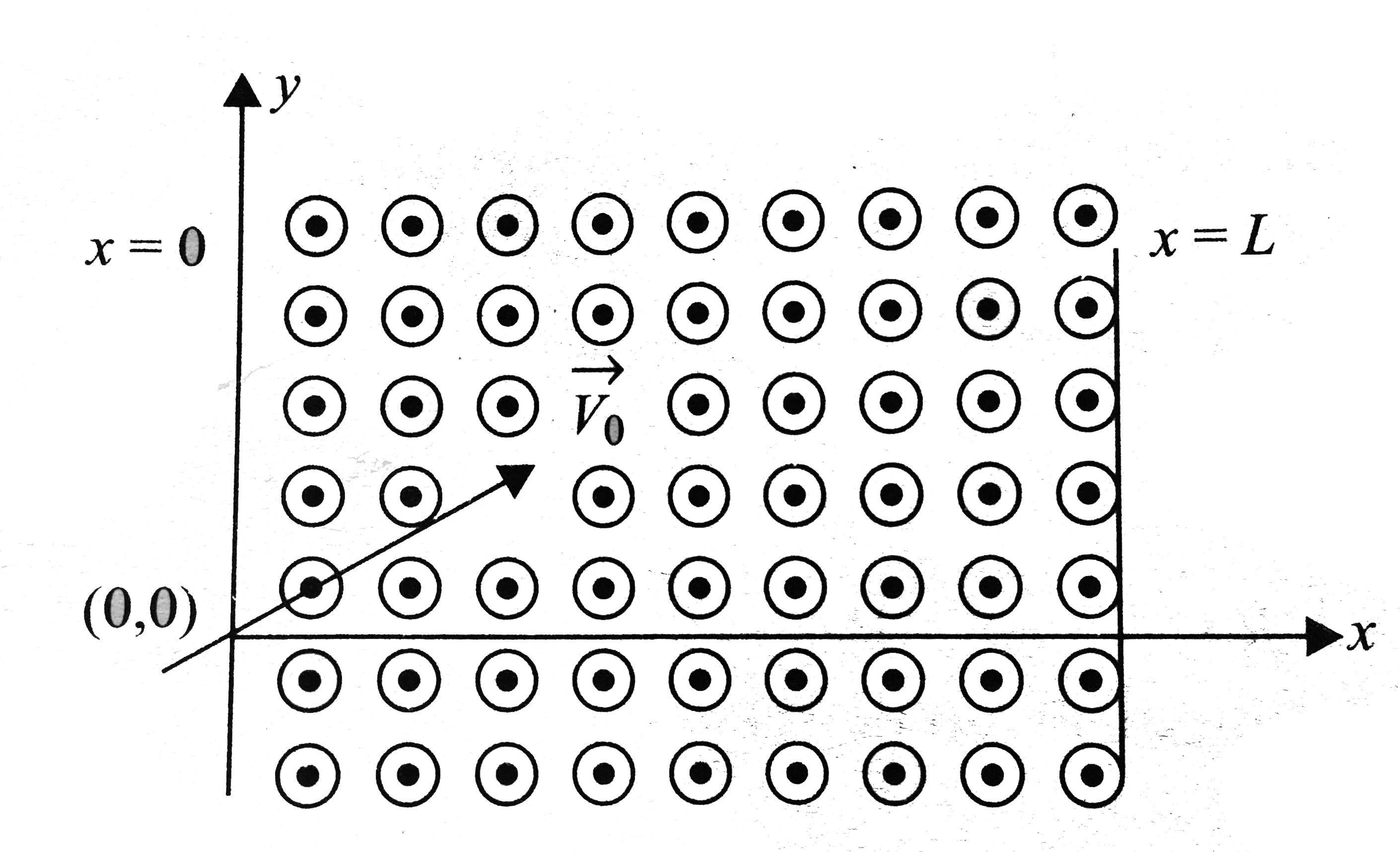
The maximum and minimum values of L such that velocity of emerging particle makes angle π/3 with the y-axis areALmin=10cm,Lmax=∞BLmin=20cm,Lmax=40cmCLmin=10cm,Lmax=20cmDLmin=20cm,Lmax=∞A particle is released from the origin with a velocity vˆe(i). The electric field in the region is Eˆe(i) and magnetic field is Bˆk. Then
AIf v=0andE=0 then particle will execute a circular path.BIf v=0,E≠0 then particle is positively charged then it executes clockwiseCIf v=0 and E≠0 then the particle will execute a cycloidal motion in the x-y plane.DIf v>0 and E≠0 and the particle is positievely charged and B>0 then the particle wil excute anticlockwise anticlock wise circle as seen from +z direction.
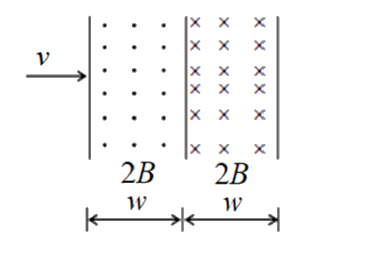
The figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View SolutionLet y>0 be the region of space with a uniform and constant magnetic field Bˆk. A particle with charge and mass m travels along the y-axis and enters in magnetic field at origin with speed v0 in region in particle is subjected to an additional friction force →F=−k→v. Assume that particle remains in region y>0.
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA particle of the mass m and cgharge q moves with a constant velocity v along the positive x−direction.Itentersaregionconta∈∈gauniformmag≠ticfieldBdirectedalongtheminiμmvalueofvrequiredsotˆthepartic≤canjustentertheregion xgtb is
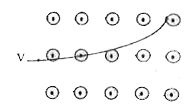
View SolutionA particle enters the region of a uniform magnetic field as shown in figure. The path of the particle inside the field is shown by dark line. The particle is :
View Solution

