A thin beam of charged particles in incident normally on the boundry of a region containing a uniform magnetic field as shown.The beam comprise of mono energetic and particles, each possessing a kinetic energy .Neglecting interaction between particles of the beam, find the separation between the points on line where the and particles emerge out of the magnetic field.(express your answer in terms of ,where all terms have their usual meanings.)
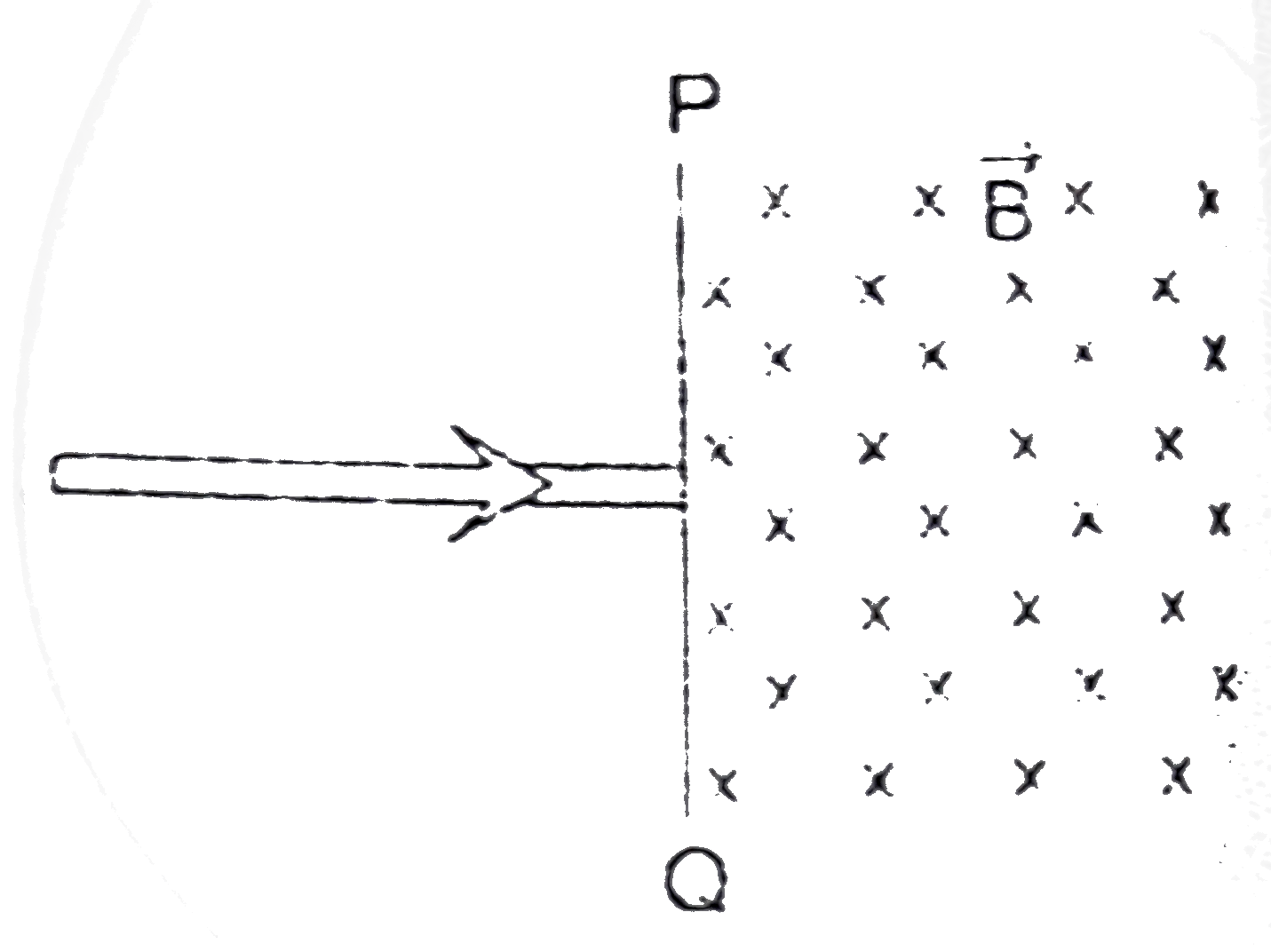
The correct Answer is:
Separation betweeen particle

Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Exercise-3 PART-3
Explore 29 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
Knowledge Check
A particle enters the region of a uniform magnetic field as shown in figure. The path of the particle inside the field is shown by dark line. The particle is :
 Aelectrically neutralBpositively chargedCnegatively chargedDinformation given is inadequate
Aelectrically neutralBpositively chargedCnegatively chargedDinformation given is inadequateIf an α-particle is projected normally through a uniform magnetic field, then the path of the α-particle inside the field will be
AcircularBparabolicCellipticalDa straight lineA protn and an alpha particle enter into a uniform magnetic field with the same velocity. The period of rotation of the alpha particle will be
Afour times that of protonBtwo times that of protonCthree times that of protonDsame as that of proton
A beam of equally charged particles after being accelerated through a voltage V enters into a magnetic field 'B' as shown. It is found that all the particles hit the plate between X and Y. Find the ration between the masses of the heaviest and lightest particles of the beam.
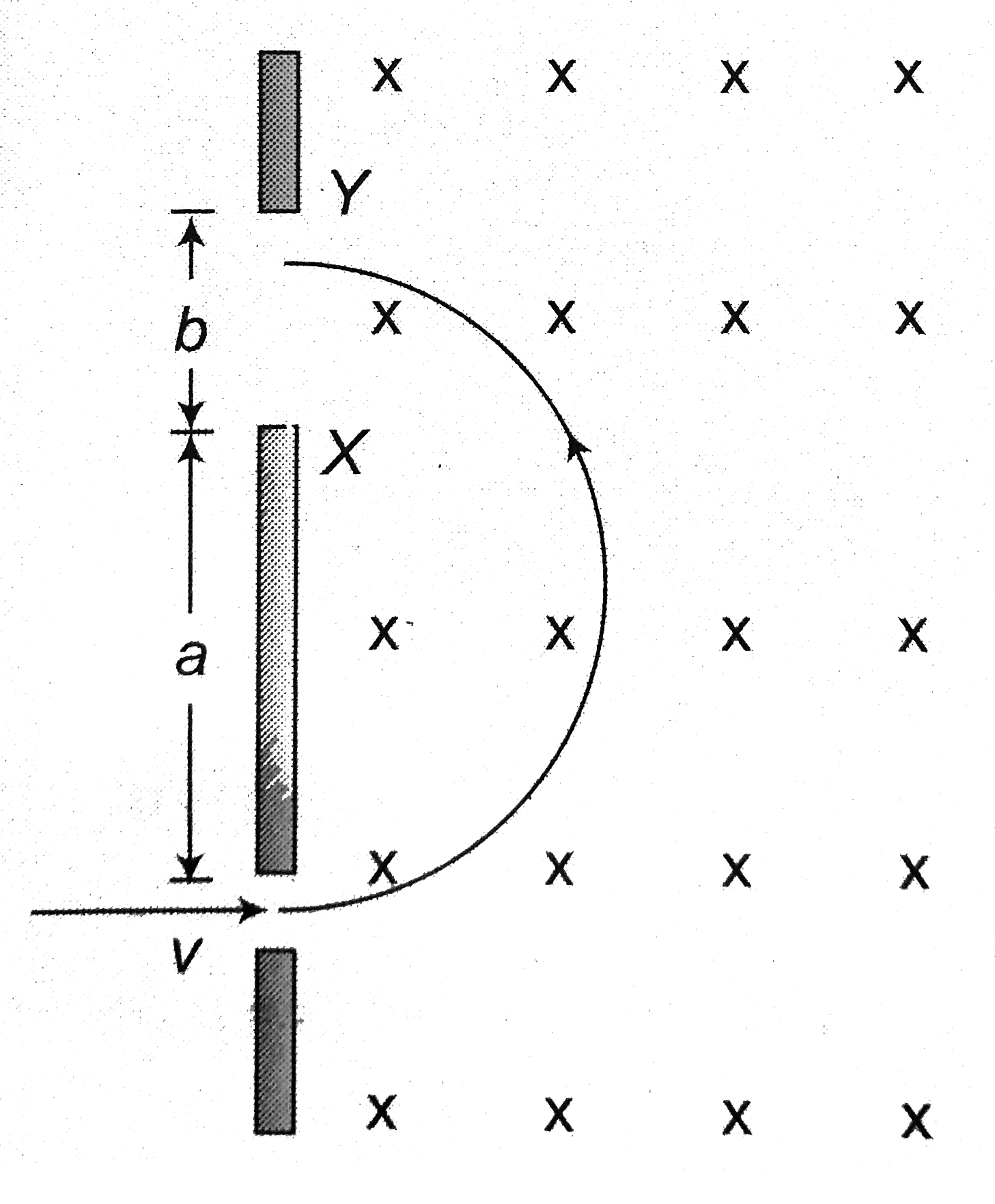
View SolutionA beam of equally charged particles after being accelerated through a voltage V enters into a magnetic field B as shown in Fig. 1.31. It is found that all the particles hit the plate between C and D. Find the ratio between the masses of the heaviest and lightest particles of the beam.

View SolutionA proton and an α- particle is projected with equal kinetic energy in transverse uniform magnetic field B. The ratio of radii of proton to that of alpha particle is
View SolutionA neutral particle at rest in a magnetic field decays into two charged particles of different mass. The energy released goes into their kinetic energy. Then what can be the path of the particles. Neglect any interaction between the two charges.
View SolutionA charged particle having kinetic energy E enters normally a region of uniform magnetic field between two plates P1 and P2 as shown in the figure. If the particle just misses hitting the plate P2, then the magnetic field B in the region between the plates is
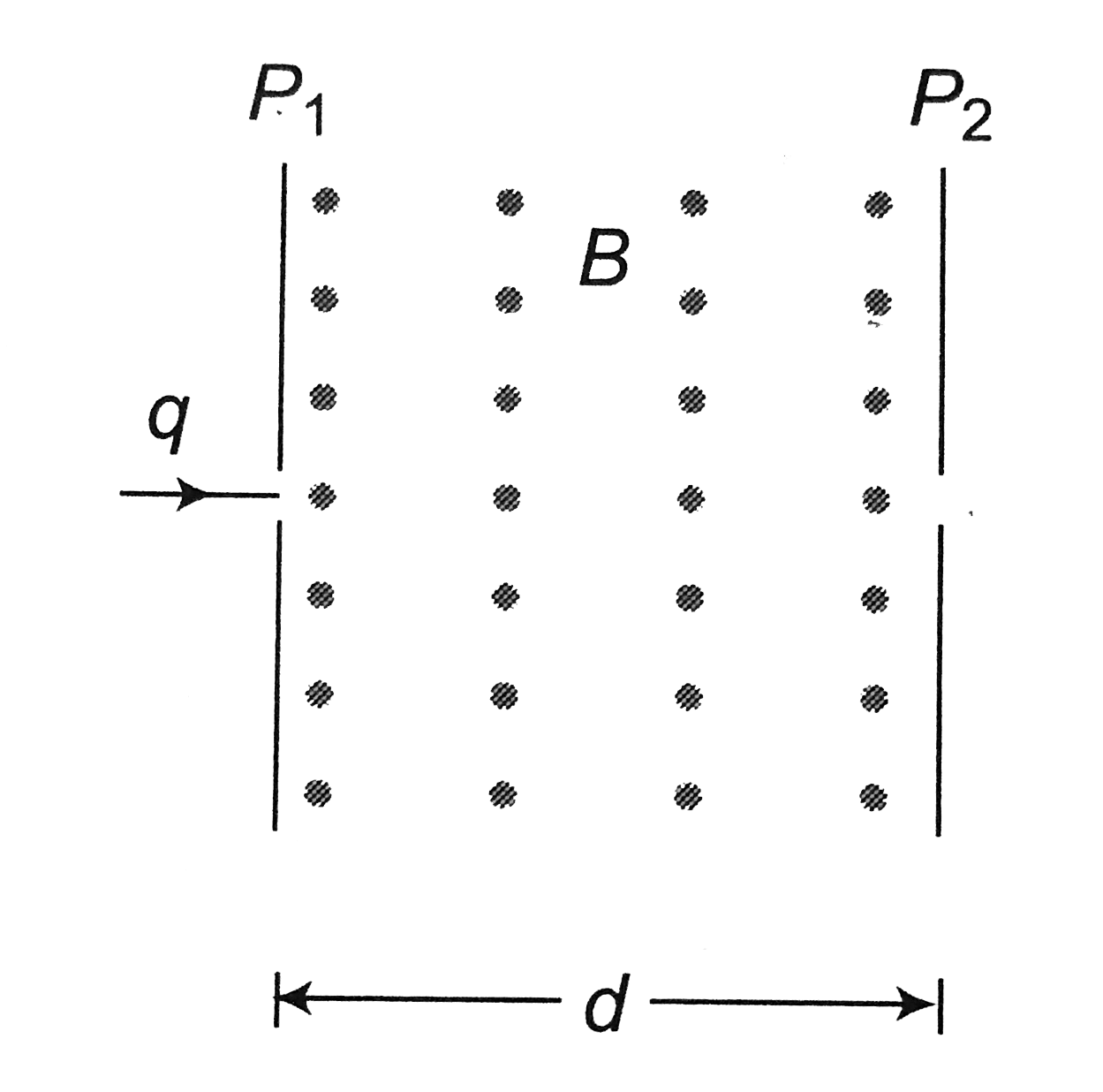
View Solution

_PHY_E06_050_Q01.png)