A beam of equally charged particles after being accelerated through a voltage V enters into a magnetic field 'B' as shown. It is found that all the particles hit the plate between X and Y. Find the ration between the masses of the heaviest and lightest particles of the beam.
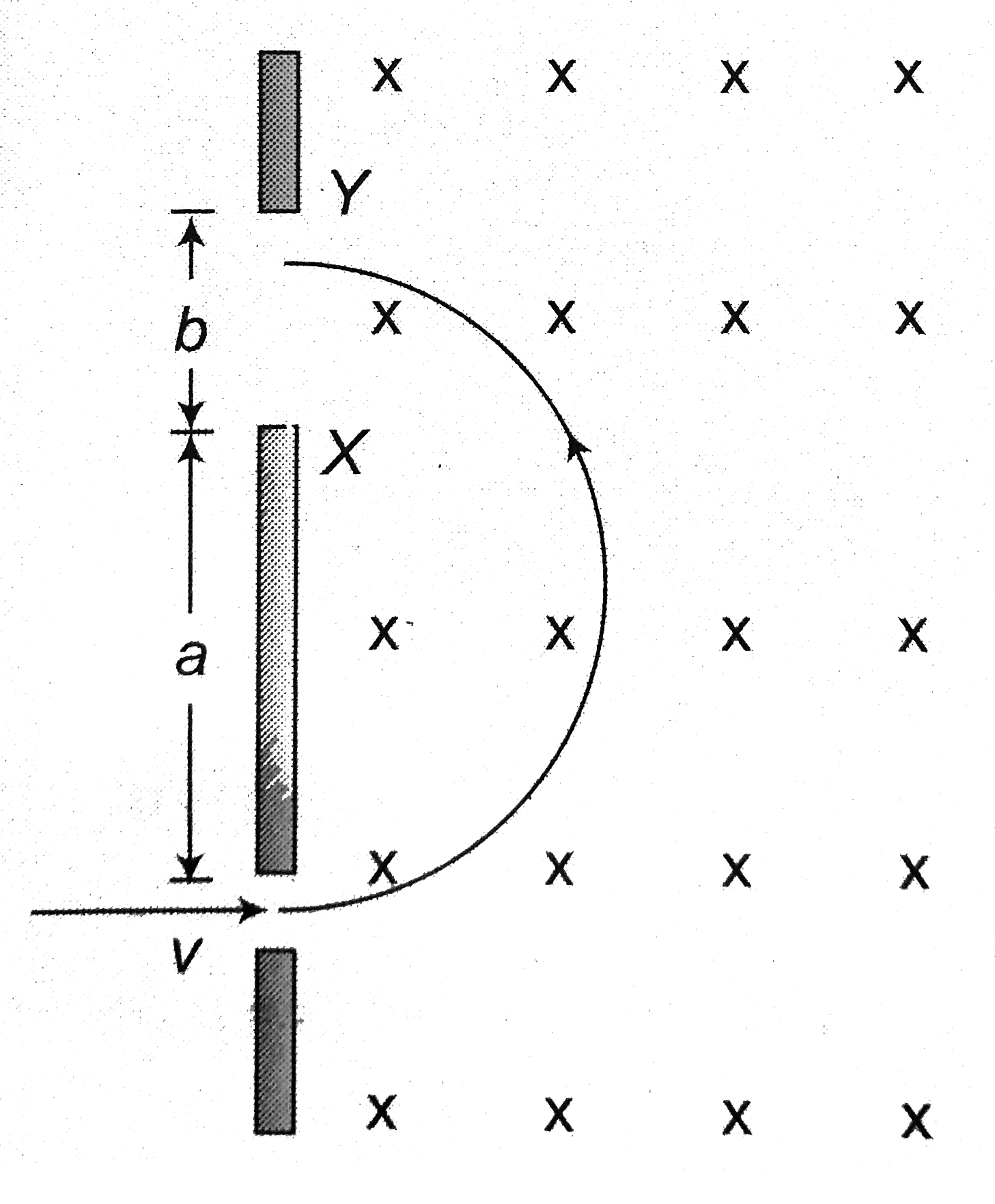
R=mvBq=√2mKBq=√2mqVBq
R∝m
The radius of heaviest particle R1=a+b
The radius of lightest particle R2=a
R1R2=√m1m2
a+ba=√m1m2
m1m2=(a+ba)2
Topper's Solved these Questions
Similar Questions
A beam of equally charged particles after being accelerated through a voltage V enters into a magnetic field B as shown in Fig. 1.31. It is found that all the particles hit the plate between C and D. Find the ratio between the masses of the heaviest and lightest particles of the beam.

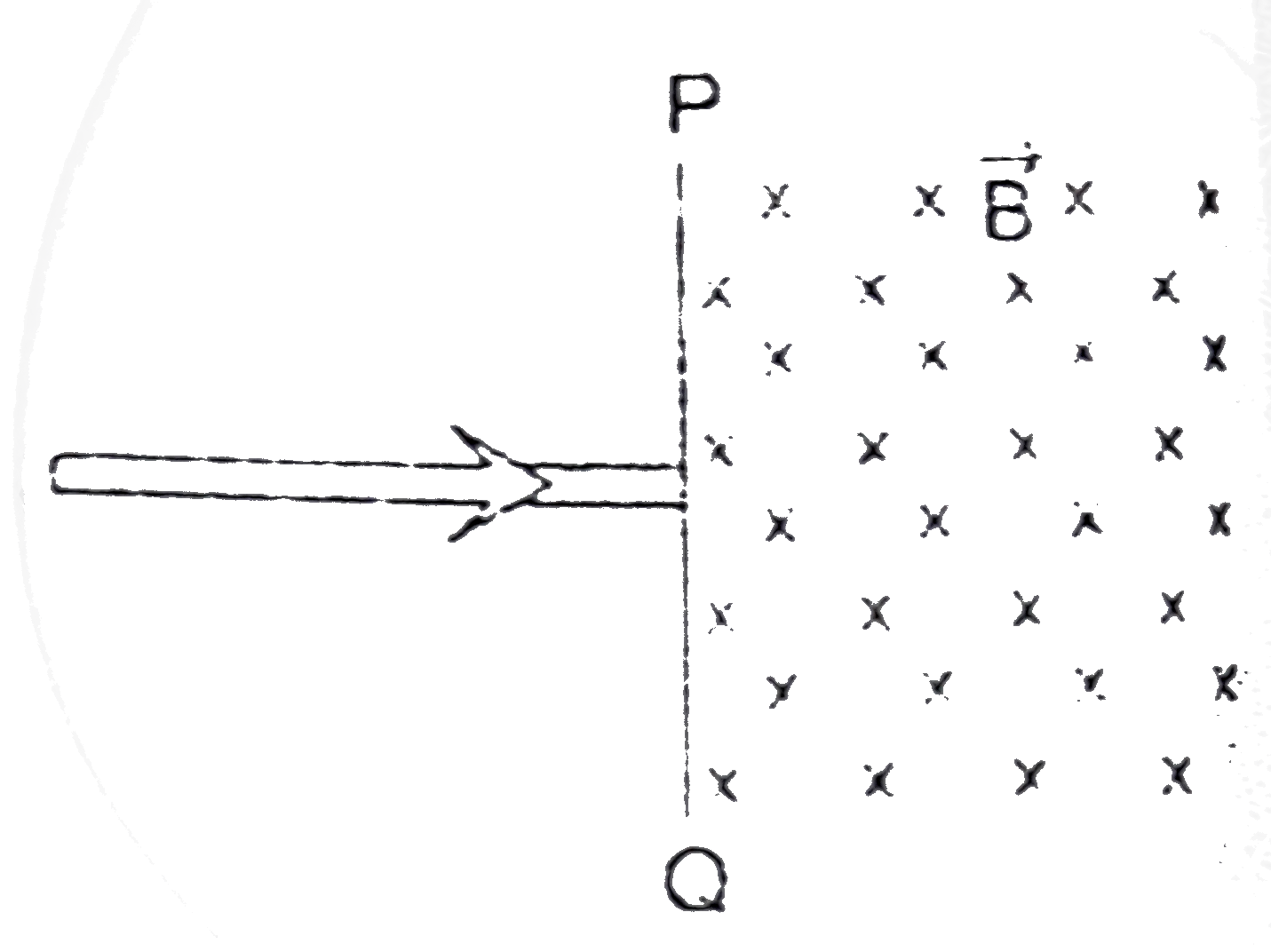
View SolutionA thin beam of charged particles in incident normally on the boundry of a region containing a uniform magnetic field as shown.The beam comprise of mono energetic α and β(−) particles, each possessing a kinetic energy T.Neglecting interaction between particles of the beam, find the separation between the points on line PQ where the α and β particles emerge out of the magnetic field.(express your answer in terms of T,B,α(2e,mα)&β−(−e,me),where all terms have their usual meanings.)
View Solution
Knowledge Check
A charge particle after being accelerated through a potential difference V enters in a uniform magnetic field and moves in a circle of radius r. If V is doubled, the radius of the circle will become
A2rB√2rC4 rDr√2A charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
 ARπθvBR(π−2θ)vCR(π+2θv)D2Rθv
ARπθvBR(π−2θ)vCR(π+2θv)D2RθvA charged particle, having charge q1 accelerated through a potential difference V enters a perpendicular magnetic field in which it experiences a force F. It V is increased to 5V, the particle will experience a force
AFB5FCF5D√5F
A beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
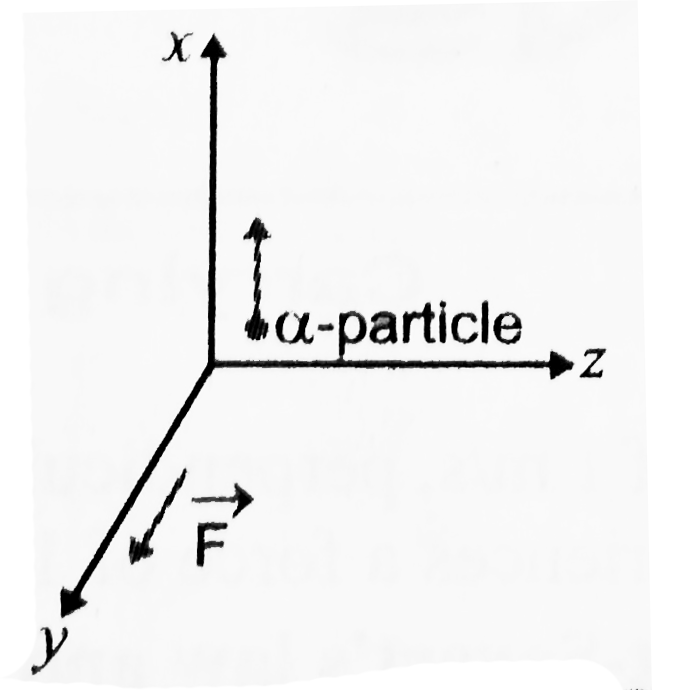
View SolutionA charged particle , having charge q accelerated through a potential difference V enters a perpendicular magnetic field in which it experiences a force F. If V is increased to 5V, the particle will experience a force.
View SolutionA proton and α particle, after accelerating through same potential difference enters into a uniform magnetic field perpendicular to their velocities, find the radius ratio of proton and α particle:-
View SolutionA charged particle having kinetic energy E enters normally a region of uniform magnetic field between two plates P1 and P2 as shown in the figure. If the particle just misses hitting the plate P2, then the magnetic field B in the region between the plates is
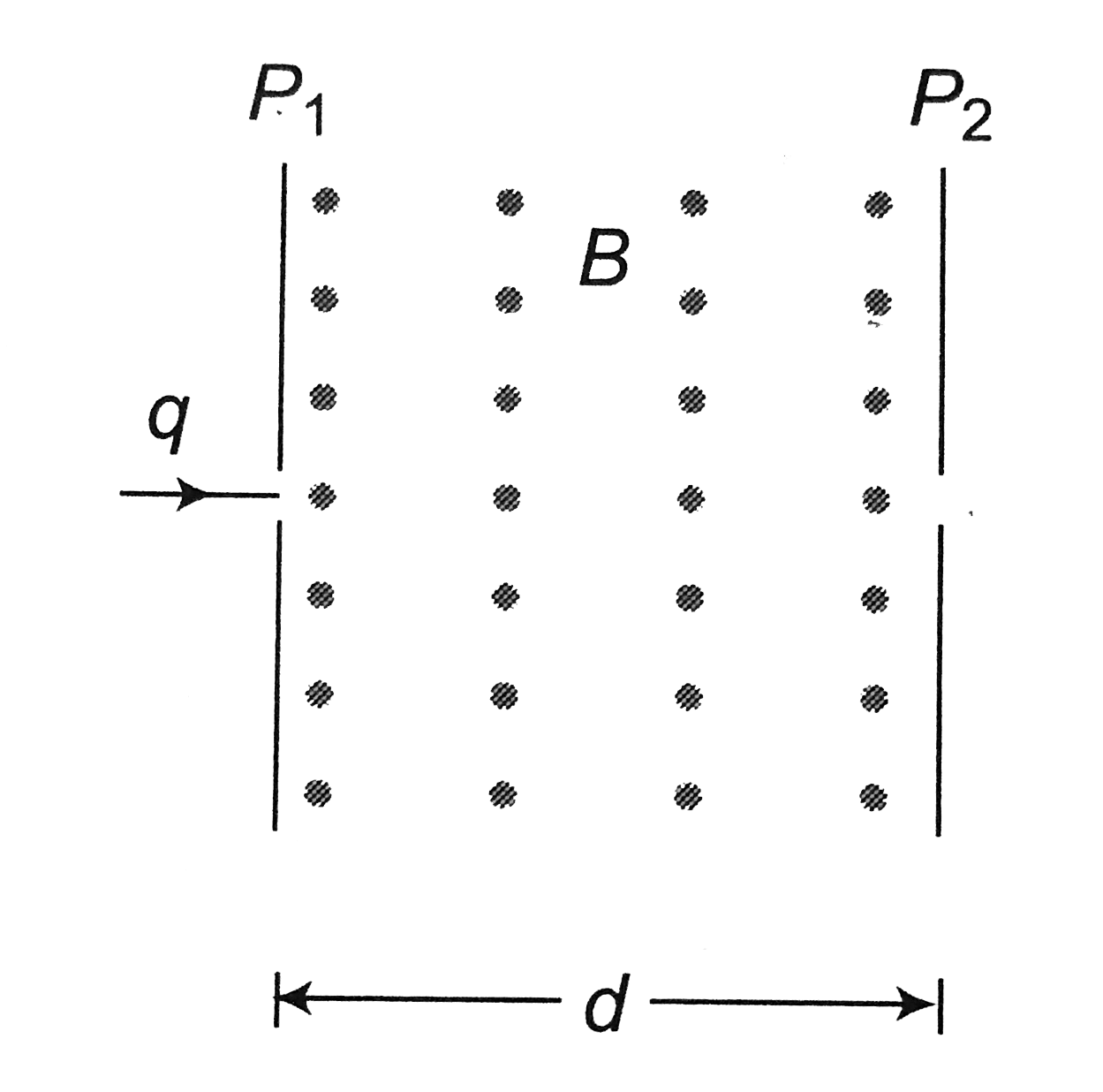
View SolutionA charged particle, having charge q1 accelerated through a potential difference V enter a perpendicular magnetic field region in which it experiences a force F. If V is increased to 5V, the particle will experience a force
View Solution
