A uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
For small amplitude the angular motion is nearly simple harmonic and the time period is given by
T=2π√1mg(l/2)=2π√(ml2/3)mg(l/2)=2π√2l3g=π√2×1.00m3×10m/s2=2π√15s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Solved Miscellaneous Problems
Explore 9 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Board Level Exercise
Explore 24 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
Knowledge Check
A uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
A1.60secB1.80 secC2.0 secD2.40 secA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23mAn infinite nonconducting sheet has surface charge density s. There is a small hole in the sheet as shown in the figure. A uniform rod of length l having linear charge density λ is hinged in the hole as shown. If the mass of the rod is m, then the time period of oscillation for small angular displacement is
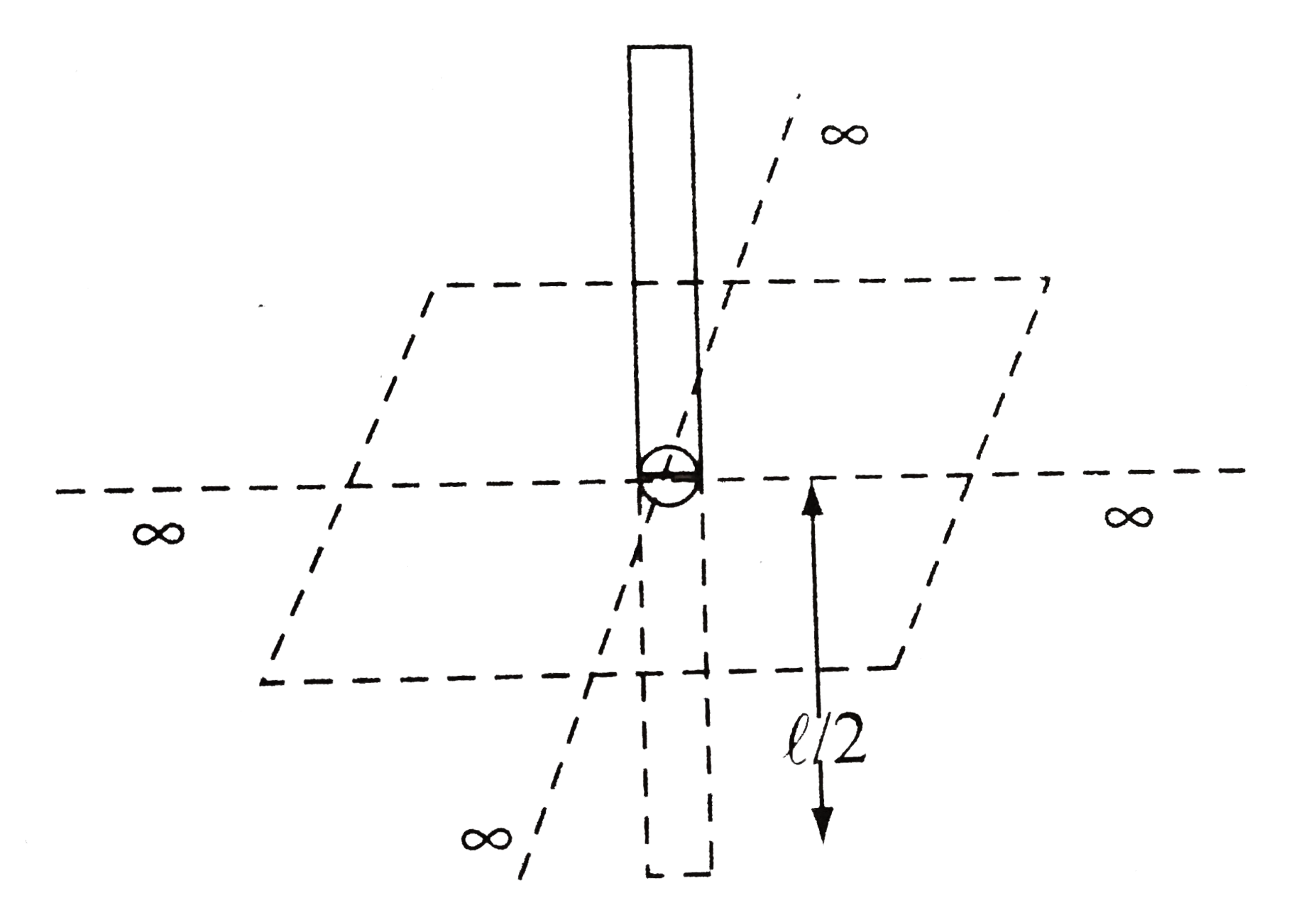 Aπ√mε03σλB2π√2mε03σλCπ2√mε03σλD4π√mε03σλ
Aπ√mε03σλB2π√2mε03σλCπ2√mε03σλD4π√mε03σλ
A uniform rod of length 2.0 m is suspended through its endpoint about which it performs small angular oscillations in the vertical plane, its time period is nearly
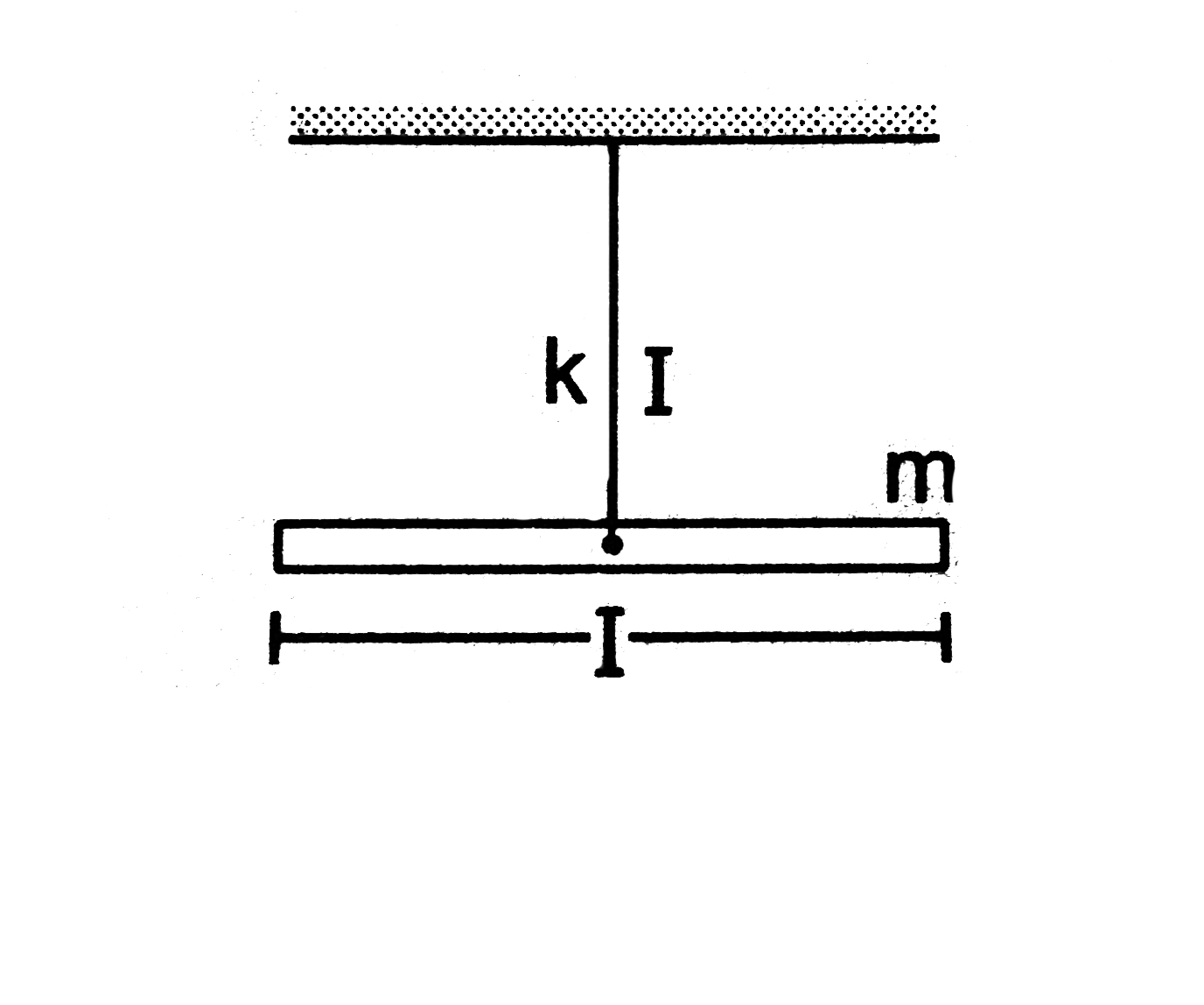
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
View SolutionA uniform rod of length l is pivoted distance x from the top of the rod . Neglecting friction find the (a) value of x for minimum period of oscillation, (b) minimum period of oscillation of the rod.

View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
View Solution

