A particle of mass 0.50kg executes a simple harmonic motion under a forve F=−(50n/m)x. If crosses the centre of oscillation with a speed of 10m/s, find the amplitude of the motion.
The kinetic energy of the particle when it is the centre of oscillation is
E=12mv2,=12(0.50kg)(10m/s)2,=25J.
The potential energy is zero here. At the maximum displacement x=A, the speed is zero and hence the kinetic enery is zero. The potential energy here is 12kA2. As there is no loss of energy.
12kA2=25J.......(i)
The force on the particle is given by
F=−(50N/m)x.
Thus, the spring constant is k=50N/m
Equation (i) gives
12(50N/m)A2=25J or, A=1m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Solved Miscellaneous Problems
Explore 9 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Board Level Exercise
Explore 24 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
A particle of mass 0.50 kg executes a simple harmonic motion under a force F = – (50 N/m)x. If it crosses the centre of oscillation with a speed of 10 m/s, find the amplitude of the motion.
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
View Solution
Knowledge Check
A particle of mass 0.1 kg executes SHM under a for F=(−10x) N. Speed of particle at mean position 6m/s. Then amplitude of oscillations is
A0.6 mB0.2mC0.4mD0.1mA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
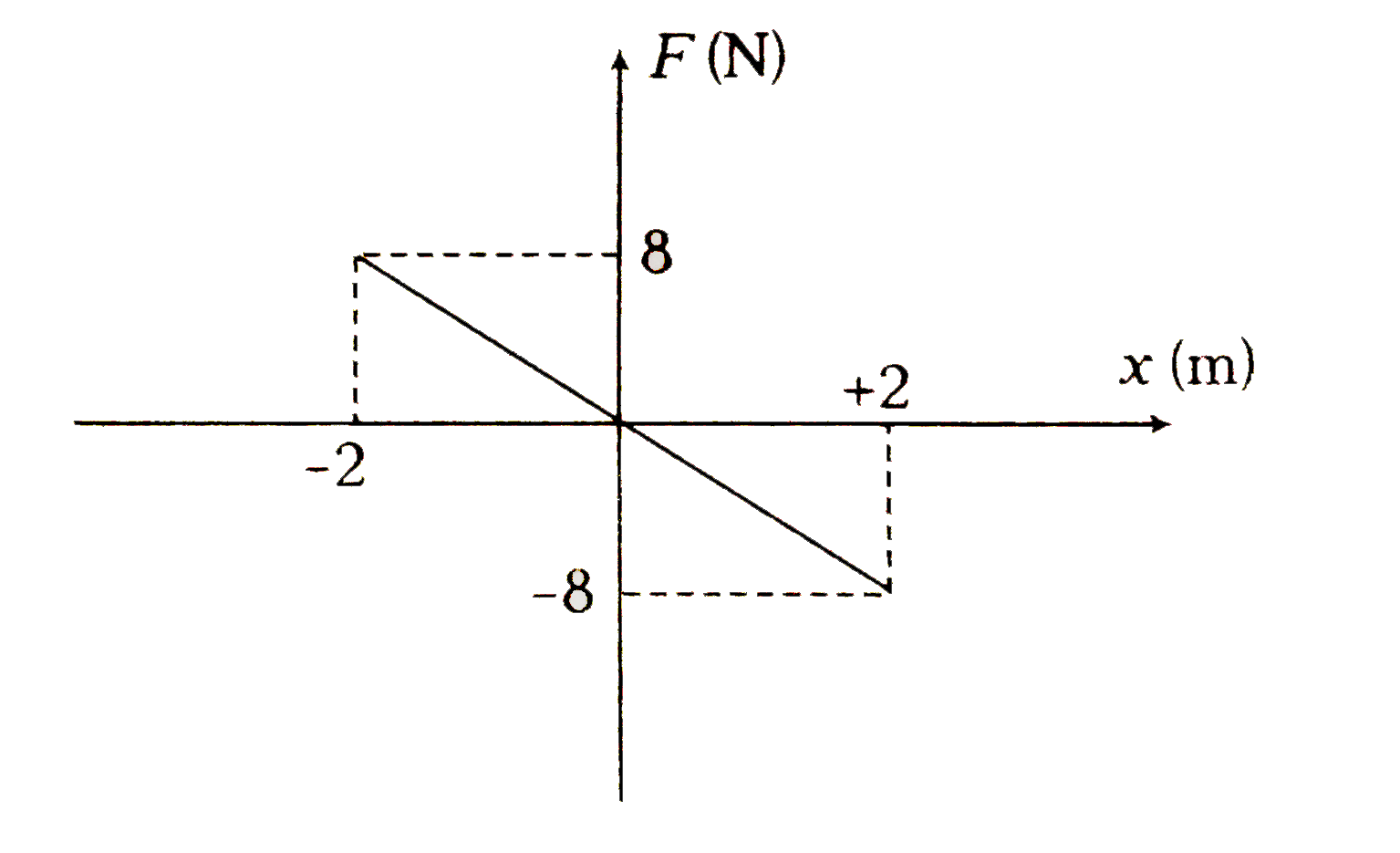 A1.05 sB0.52 sC0.25 sD0.31 s
A1.05 sB0.52 sC0.25 sD0.31 sA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
 A2π5sB2√2π5sC√2π5sD4π5s
A2π5sB2√2π5sC√2π5sD4π5s
A particle executes simple harmonic motion of period 16s. Two seconds later after it passes through the center of oscillation its velocity is found to be 2m/s. Find the amplitude.
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
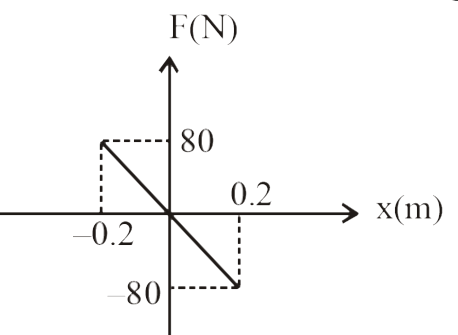
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle of mass 0.2kg executes simple harmonic motion along a path of length 0.2m at the rate of 600oscillations per minute. Assume at t=0. The particle start SHM in positive direction. Find the kinetic potential energies in joules when the displacement is x=A/2 where, A stands for the amplitude.
View SolutionA particle of mass 0.2 kg executes SHM under a force of F = - 20x N. If speed of particle at mean position is 12 m/s then the amplitude of oscillations is
View Solution