D is a point on the side BC of a triangle ABC such that ∠ADC=∠BAC. Show that CA2=CB.CD.
To solve the problem, we need to show that CA2=CB⋅CD given that ∠ADC=∠BAC.
1. Identify the triangles: We have triangle ABC and point D on side BC. We know that ∠ADC=∠BAC.
2. Establish similarity: Since ∠ADC=∠BAC and ∠ACD is common to both triangles ADC and ABC, we can conclude that:
△ADC∼△ABC
This means that the corresponding sides of these triangles are proportional.
3. Set up the proportion: From the similarity of triangles, we can write the following proportions:
ADAB=DCAC=ACBC
4. Focus on the relevant ratios: We will use the ratios ACBC and DCAC for our proof. From the similarity, we can express:
DCAC=ADAB
Rearranging gives us:
DC=AC⋅ADAB
5. Express CA2: We know that CA2 can be expressed in terms of CB and CD. We will use the proportion:
ACBC=DCAC
Cross-multiplying gives us:
AC⋅AC=CB⋅DC
Which simplifies to:
CA2=CB⋅CD
6. Conclusion: Therefore, we have shown that:
CA2=CB⋅CD
Hence, the statement is proved.
△ADC∼△ABC
This means that the corresponding sides of these triangles are proportional.
ADAB=DCAC=ACBC
DCAC=ADAB
Rearranging gives us:
DC=AC⋅ADAB
ACBC=DCAC
Cross-multiplying gives us:
AC⋅AC=CB⋅DC
Which simplifies to:
CA2=CB⋅CD
CA2=CB⋅CD
Hence, the statement is proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let D be the middle point of the side BC of a triangle ABC. If the triangle ADC is equilateral, then a2:b2:c2 is equal to
A1:4:3B4:1:3C4:3:1D3:4:1
Triangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
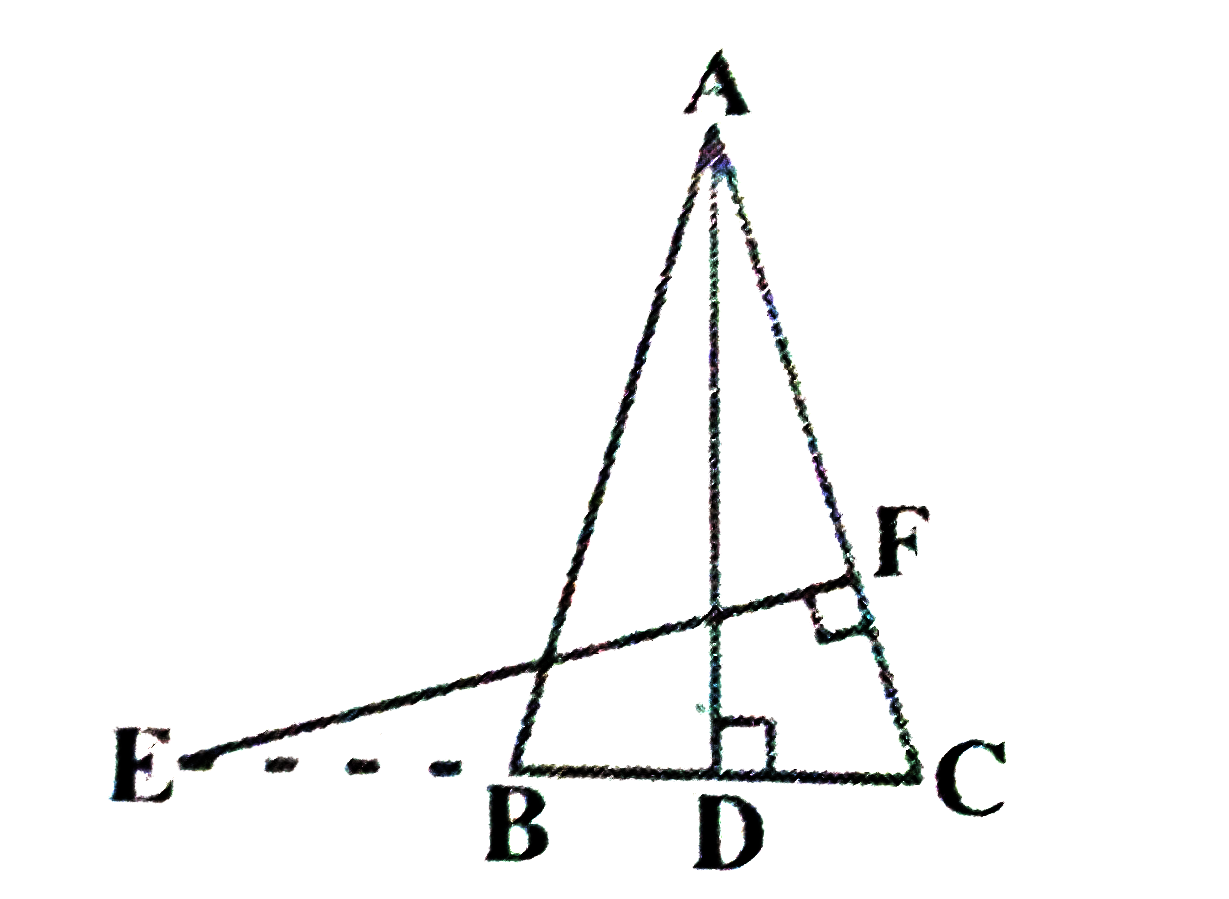
View SolutionIn a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionIf D is the mid-point of the side BC of triangle ABC and AD is perpendicular to AC , then 3b2=a2−c (b) 3a2=b23c2 b2=a2−c2 (d) a2+b2=5c2
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionTwo triangles ABC and DEF such that ∠A=∠D,∠B=∠Eand∠C=∠F. Then
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960
View Solution