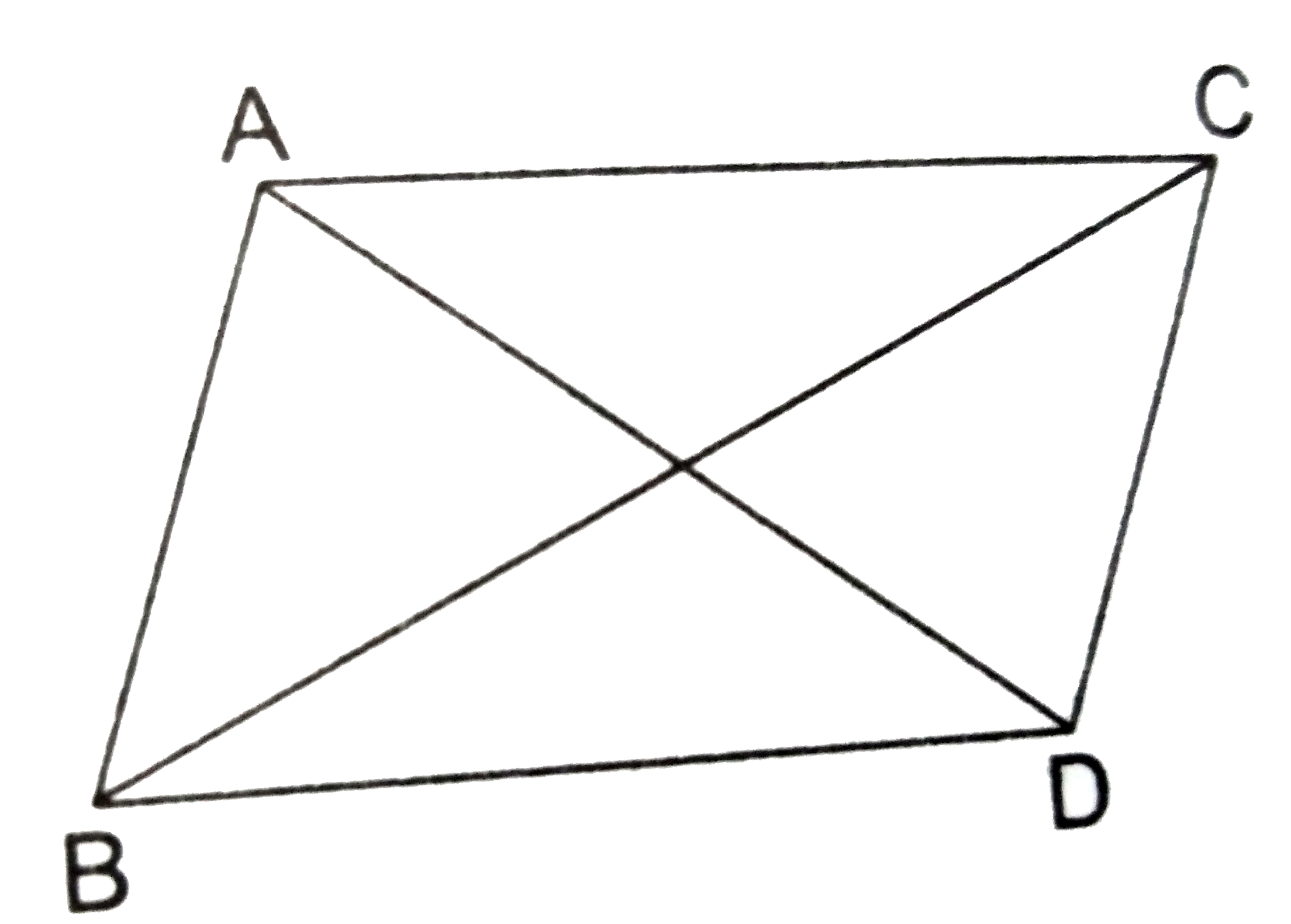
Triangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.

ar(△ABC)=ar(△DBC)
12×BC×AE=12×BC×DF
AE=DF→eq(1)
In △AEOand△DFO
AE=DF
∠AEO=∠DFO→(eq (1) )
∠AOE=∠DOF→(900 each)
byAAS axion
OA=OD→(vertically opposite angle)
O is the mid point
∴BC bisects AD
Topper's Solved these Questions
Similar Questions
Triangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionTriangles on the same base and between the same parallels are equal in area. GIVEN : Two triangles ABC and PBC on the same base BC and between the same parallel lines BC and AP. TO PROVE : ar(ABC)=ar(PBC) CONSTRUCTION : Through B, draw BDCA intersecting PA produced in D and through C, draw CQBP, intersecting line AP in Q.
View Solutionshow that in a triangle △ABC:acotA+bcotB+ccotC=2(R+r).
View SolutionABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.
View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC,PQAB AND PRBD ARE DRAWN. They meet AC in Q and DC in R respectively. Prove that QRAD.
View Solution
