An insulated cylinder is divided into three parts A, B and C. Pistons 1 and 2 are connected by a rigid rod and can slide without friction inside the cylinder. Piston 1 is perfectly conducting while piston 2 is perfectly insulating. Equal quantity of an ideal gas is filled in three compartments and the state of gas in every part is same (P0V0T0). Adiabatic exponent of the gas is g = 1.5. The compartment B is slowly given heat through a heater H such that the final volume of gas in part C becomes 4V09
(a) Calculate the heat supplied by the heater.
(b) Calculate the amount of heat flow through piston 1.
(c) If heater were in compartment A, instead of B how would your answers to (a) and (b) change?
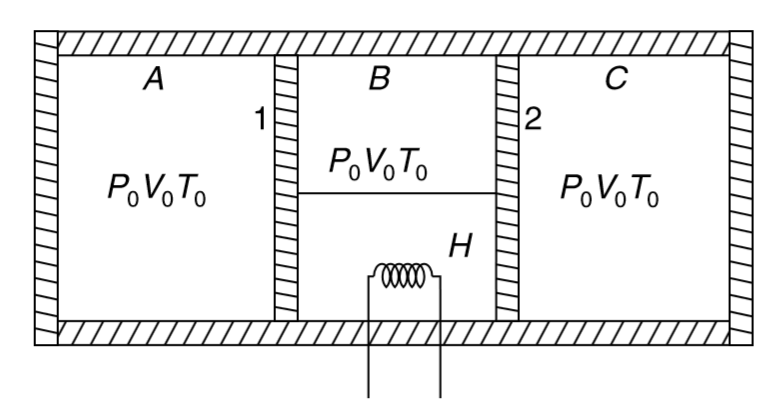
The correct Answer is:(i) PA=PC=278P0,PB=214P0 (ii) TA=TB=214T0,TC=32T0 (iii) 18P0V0(iv)WA=P0V0,WB=0 (v)172P0V0
For compartment C
P0Vγ0=P(4V09)γ ⇒P=278P0
⇒P0Tγ/1−γ0=PTγ/1−γ
P0T−30=(278P0)×T−3⇒T=32T0
For compartment A
PA=278P0
P0V0RT0=P1V1RT1
⇒T1=278P0(2V0−4V09)R×RT0P0V0=T1=214T0
For compartment B
P0V0T0=P1V1T1⇒P0V0T0=P1V0(214T0)⇒P1=214P0
Final pressure in A278P0
Final pressure in B214P0
Final pressure in C32P0
(ii) Final temperature in A=214T0
Final temperature in B=214T0
Final temperature in C=32T0
(iii) Heat supplied by heater = (ΔU+W)
Q=(ΔU1+W1)+(ΔU2+W2)+0
=(ΔU1−W3)+(ΔU2+0)
=ΔU1+ΔU2−W3
= n1RΔTγ1−1+n2RΔTγ2−1−(n3RΔTγ3−1)
=172P0V0+172P0V0+P0V0=18P0V0
(iv) Work done by gas in chamber B=0
Work done by gas in chamber C=−ΔU=−nRΔTγ−1=−P0V0
Work done by gas in chamber A=(−)Wchamber=−(P0V0)=P0V0
(v) Heat flowing across piston-I = ΔU2=172P0V0
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B)
58 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
An aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionA vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300K. The ratio of the average rorational kinetic energy per O2 molecules to that per N2 molecules is
View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionWhat will be the number of electron passing through a heater wire in one minute, if it carries a current of 8A
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA closed hollow insulated cylinder is filled with gas at 0^(@)C and also contains an insulated piston of negligible weight and negligible thickness at the middle point. The gas on one side of the piston is heated to 100^(@)C . If the piston moves 5 cm the length of the hollow cylinder is
View SolutionA heat-conducting piston can freely move inside a closed thermally insulated cylinder with an ideal gas. In equilibrium the piston divides the cylinder into two equal parts, the gas temperature being equal to T0. The piston is slowly displaced. Find the gas temperature as a function of the ratio η of the volumes of the greater and smaller sections. The adiabatic exponent of the gas is equal to γ.
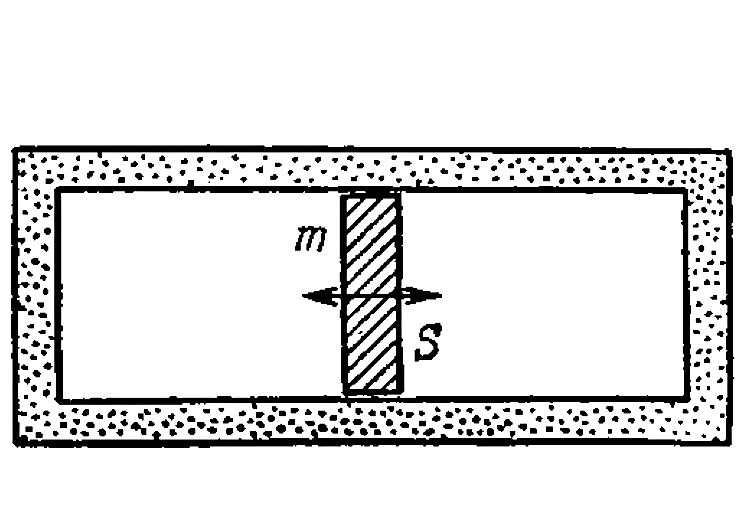
View SolutionIn a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass m and cross − sectional area S (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime V0 . The gas ppressure is p0. The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V_(0) and pressure P_(0) in equilibrium Assume the sepatator to move without friction. If the piston is slightly displaced by x, the net force acting on the piston is
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
The time period of oscillation for small displacements of the piston is
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T_(0) and pressure P_(0) occupies a volume V_(0) in the cylinder. The atmospheric pressure is P_(0) and the atmospheric temperature is T_(1) (gt T_(0)) . Find (a) the temperature of the gas as a function of time (b) the height raised by the piston as a function of time. Neglect friction and heat capacities of the container and the piston.
View SolutionAn insulated cylinder is divided into three parts A, B and C. Pistons 1 and 2 are connected by a rigid rod and can slide without friction inside the cylinder. Piston 1 is perfectly conducting while piston 2 is perfectly insulating. Equal quantity of an ideal gas is filled in three compartments and the state of gas in every part is same (P0V0T0). Adiabatic exponent of the gas is g = 1.5. The compartment B is slowly given heat through a heater H such that the final volume of gas in part C becomes 4V09
(a) Calculate the heat supplied by the heater.
(b) Calculate the amount of heat flow through piston 1.
(c) If heater were in compartment A, instead of B how would your answers to (a) and (b) change?

View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T_(0) The cylinder B contain identical gas at same temperature T_(0) but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V_(0) . The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T_(0) reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5) The mass of gas in cylinder B
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas=1.5)

The change in internal energy of gas in cylinder A
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)

If work done by gas in cylinder B is WB & work done by gas in cylinder A is WA then
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T_(0) The cylinder B contain identical gas at same temperature T_(0) but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V_(0) . The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T_(0) reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5) What will be the compressive force in conneting rod at equilibrium
View Solution