Two cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)

If work done by gas in cylinder B is WB & work done by gas in cylinder A is WA then
WA=−WB
|WA|>|WB|
|WA|<|WB|
we can't say anything
The correct Answer is:C
P0V0=mMRT ina cylinder....(1)
PBV0=mBMRT in Bcylinder.....(2) adiabatic
P0Vγ0=Pf(V02)γ
Pf=2√2P0=PB
Divide((1))//(2) P0V0PBVB=mmBVB=32V0
P0V02√2P0(32V0)=mmB
mB=3√2m
ΔU=−W=(PfVf−PiViγ−1)=2P0V02×2√2−P0V0(3/2)−1=2(√2−1)P0V0
Fcompressive=PfArea=2√2Ps
WA=(PiVi−PfVfγ−1)=P0V0−2√2P0(V0/2)(3/2)−1=2P0V0(1−√2)
|WA|=0.828P0V0=P0V0(2(1−11.414)=P0V0(−0.828)=−0.828P0V0
T=C=nRT0ln(VfVi)=PfVfln(3V02V0)=2√2P0(3V02)ln(32)=3√2P0V0ln(32)
=[3√2ln(1.5)P0V0]=(4.242×0.40)P0V0
WB=1.719P0V0
|WB|=1.719P0V0
|WA|<|WB|
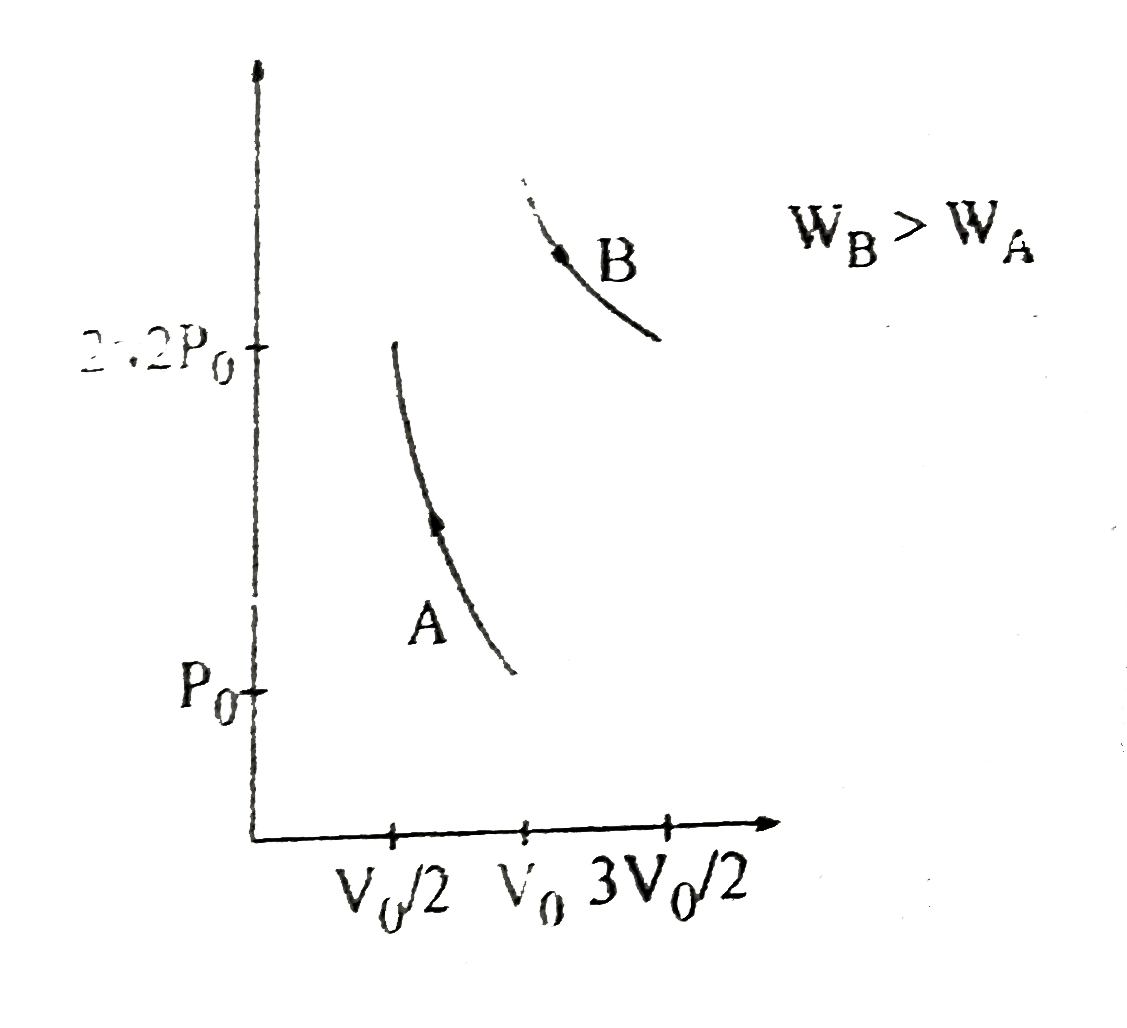
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Statement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.
View SolutionThe quantity// quantities that does //do not have mass in its// their dimentions (when we take standard 7 quantities as fundmental) is//are:
View SolutionThe manifestation of band structure in solids is due to
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T_(0) The cylinder B contain identical gas at same temperature T_(0) but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V_(0) . The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T_(0) reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5) The mass of gas in cylinder B
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas=1.5)
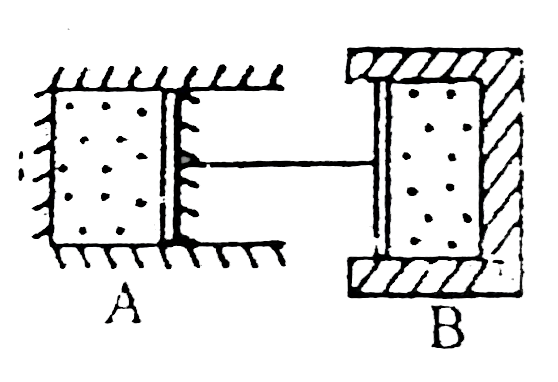
The change in internal energy of gas in cylinder A
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T_(0) The cylinder B contain identical gas at same temperature T_(0) but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V_(0) . The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T_(0) reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5) What will be the compressive force in conneting rod at equilibrium
View SolutionTwo cylinder A and B fitted with pistons contain equal number of moles of an ideal monoatomic gas at 400 K . The piston of A is free to move while that of B is held fixed . Same amount of heat energy is given to the gas in each cylinder . If the rise in temperature of the gas in A is 42 K, the rise in temperature of the gas in B is
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300 K. The piston of A is free to move, while that of B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30 K, then the rise in temperature of the gas in B is :
View SolutionA cylinder with two ends is equipped with a moving piston. The gas on one side of the piston has a mass M and the other side has a mass of 2m of the same gas. If the piston is in equilibrium state, how much volume of the cylinder will be surrounded by the greater mass of gas while the temperature is the same in the whole cylinder?
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300 K. The piston of A is free to move, while that of B is held fixed. The same amount of heat is given to the gas ineach cylinder. If the rise in temperature of the gas in A to 30 K, then the rise in temperature of the gas in B is
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move while that of B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30 K, then the rise in temperature of the gas in B is :
View SolutionTwo cylinder A and B fitted with pistons contain equal number of moles of an ideal monoatomic gas at 400 K . The piston of A is free to move while that of B is held fixed . Same amount of heat energy is given to the gas in each cylinder . If the rise in temperature of the gas in A is 42 K, the rise in temperature of the gas in B is
View Solution
