Two vertical cylinders are connected by a small tube at the bottom. It contains a gas at constant temperature . Initially the pistons are located at the same height. The diameters of the two cylinders are different . Outside the cylinder the space is vaccum . Gravitational acceleration is h,h0=20cm,m1=2kgandm2=1kg. The pistons are initially in equilibrium. If the masses of the piston are interchanged find the separation between the two pistons when they are again in equilibrium. Assume constant temperature .
_E01_299_Q01.png)
The correct Answer is:30cm
For equilibrium m1gA1+ρgh0=m2gA2+ρgh0
m1=2kg,m2=1kg⇒2A1=1A2
For final equilibrium m1gA2>m2gA1
∴m1 block will fall down
For constant temperature forces and pressure being constant Vinitial=Vfinal
h0A1+h0A2=h1A1+h2A2⇒h1=30 cm & h2=0
_E01_299_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B)
58 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
View SolutionThe piston cylinder arrangement shown contains a diatomic gas at temperature 300 K The cross sectinal area of the cylinder is 1m2. Initially the height of the piston above th base of the cyclinder is 1 m. The temperature is now raised to 400 K at constant pressure. There is no heat loss in the process..
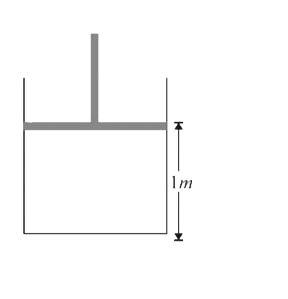
Find the new height (in m) of the piston above the base of the cylinder.
View Solution
Knowledge Check
Two diameter of the base of a cylinder is 4 cm and its height is 20 cm . The volume of the cylinder is
A176cm3B196cm3C276cm3D352cm3A gas is filled in the cylinder shown in fig. The two pistons are joined by a string. If the gas is heated, the right piston will
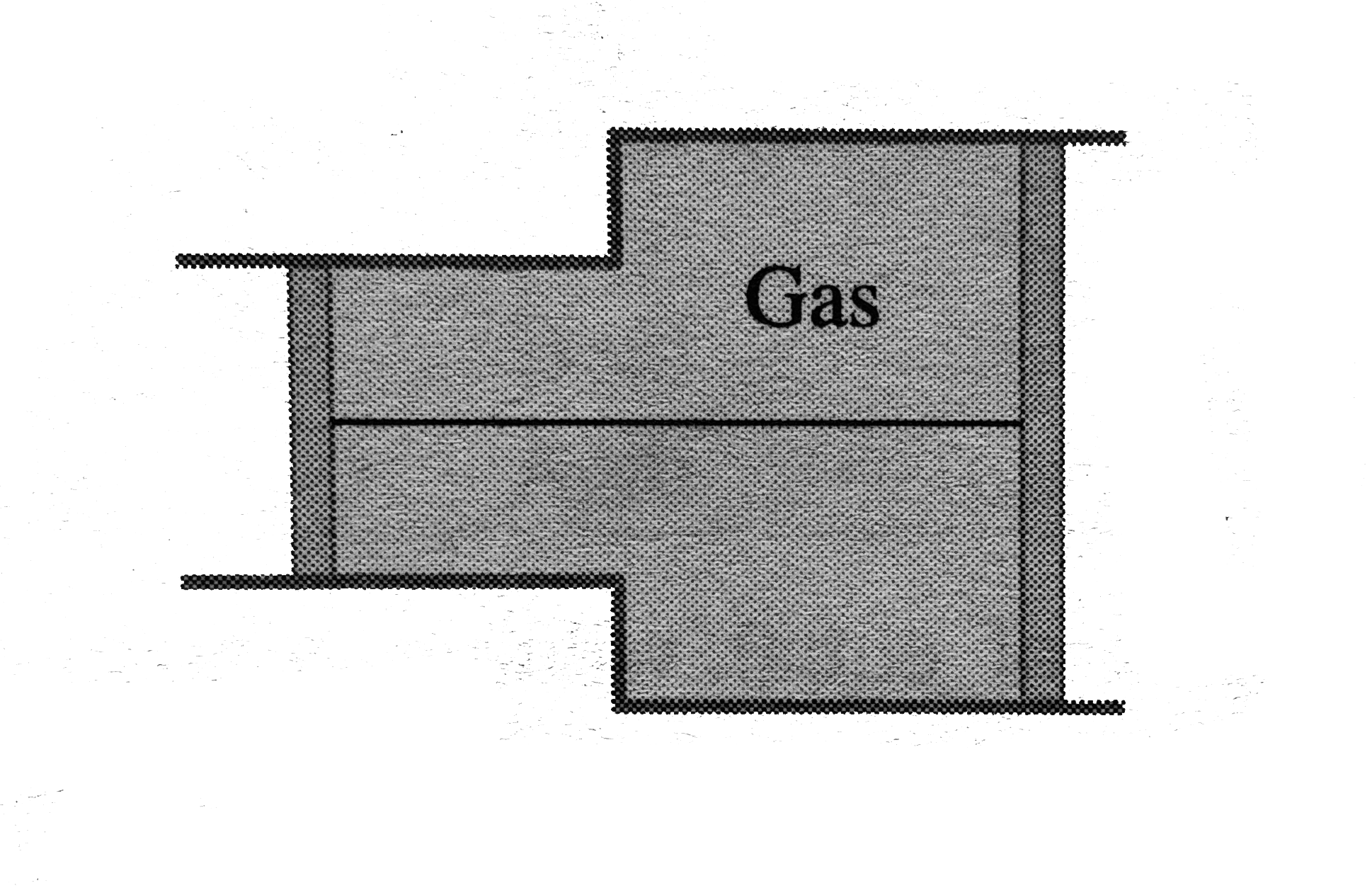 Amove toward leftBmove toward rightCremain stationaryDnone of these
Amove toward leftBmove toward rightCremain stationaryDnone of theseTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)

If work done by gas in cylinder B is WB & work done by gas in cylinder A is WA thenAWA=−WBB|WA|>|WB|C|WA|<|WB|Dwe can't say anything
Two cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5)

The mass of gas in cylinder B
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas=1.5)
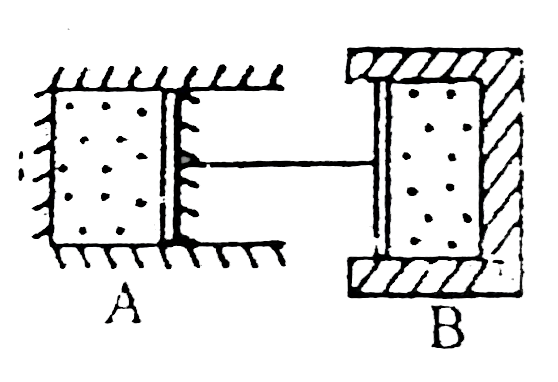
The change in internal energy of gas in cylinder A
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)
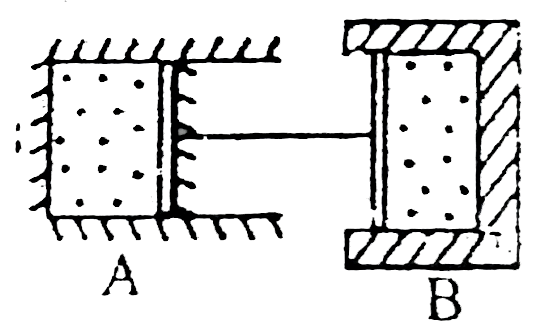
What will be the compressive force in conneting rod at equilibrium
View SolutionA gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View SolutionA cylinder fitted with a piston contains 0.2 moles of air at temperature 27∘ . The piston is pushed so slowly that the air within the cylinder remains in thermal equilibrium with the surroundings. Find the approximate work done by the system if the final volume is twice the initial volume
View Solution
