A non-conducting cylindrical vessel of length 3l is placed horizontly & is divided into three parts by two easily moving piston having low thermal conductivity as shown in figure. These parts contains H2, He and CO2 gas at initial temp. θ1=372∘C,θ2=−15∘C and θ3=157∘C respectively. If initial length and pressure of each part are l and P0 respectively. calculate final pressure and length of each part . Use : γco2=7/5
_E01_301_Q01.png)
The correct Answer is:1312P0,l1=0.6l,l2=1.5l,l3=0.9l
θ1=372∘C,θ2=−15∘C,θ3=157∘CγCO2=75
For the H2 gas P1V1RT1=P2V2RT2⇒P0Al645R=P×Al1TR…(i)
For the He gas P0Al258R=P×Al2TR....(ii)
For the CO2 gas P0Al430R=P×Al2TR....(iii)
⇒l1l2=258645=12.5 & l1l3=430645=11.5
⇒l1+l2+l3=3l⇒l1(1+2.5+1.5)=3l
l1=0.6landl2=2.5l1=1.5ll3=1.5×0.6l=0.9l
For the entire system ΔU1+ΔU2+ΔU3=0
⇒n1R(T−T1)γ1−1+n2R(T−T2)γ2−1+n3R(T−T3)γ3−1=0
⇒P×0.6l−P0l(75−1)+(P×1.5l−P0l)(53−1)+P×0.9l−P0l(75−1)=0
⇒P=1312P0
_E01_301_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (A)
Explore 73 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (B)
Explore 58 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 04 (A)
Explore 48 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Knowledge Check
A cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
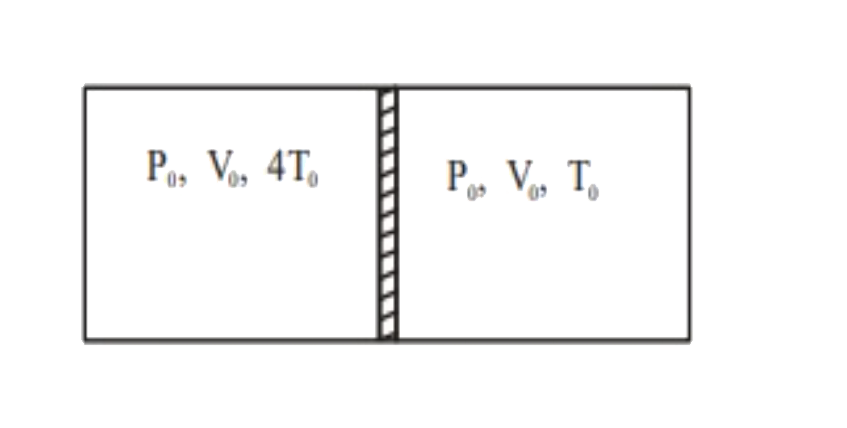 A85P0AB25P0AC56P0AD65P0A
A85P0AB25P0AC56P0AD65P0AThree identical conducting rods are connected as shown in figure. Given that θa=40∘C, θc=30∘C and θd=20∘C. Choose the correct option.
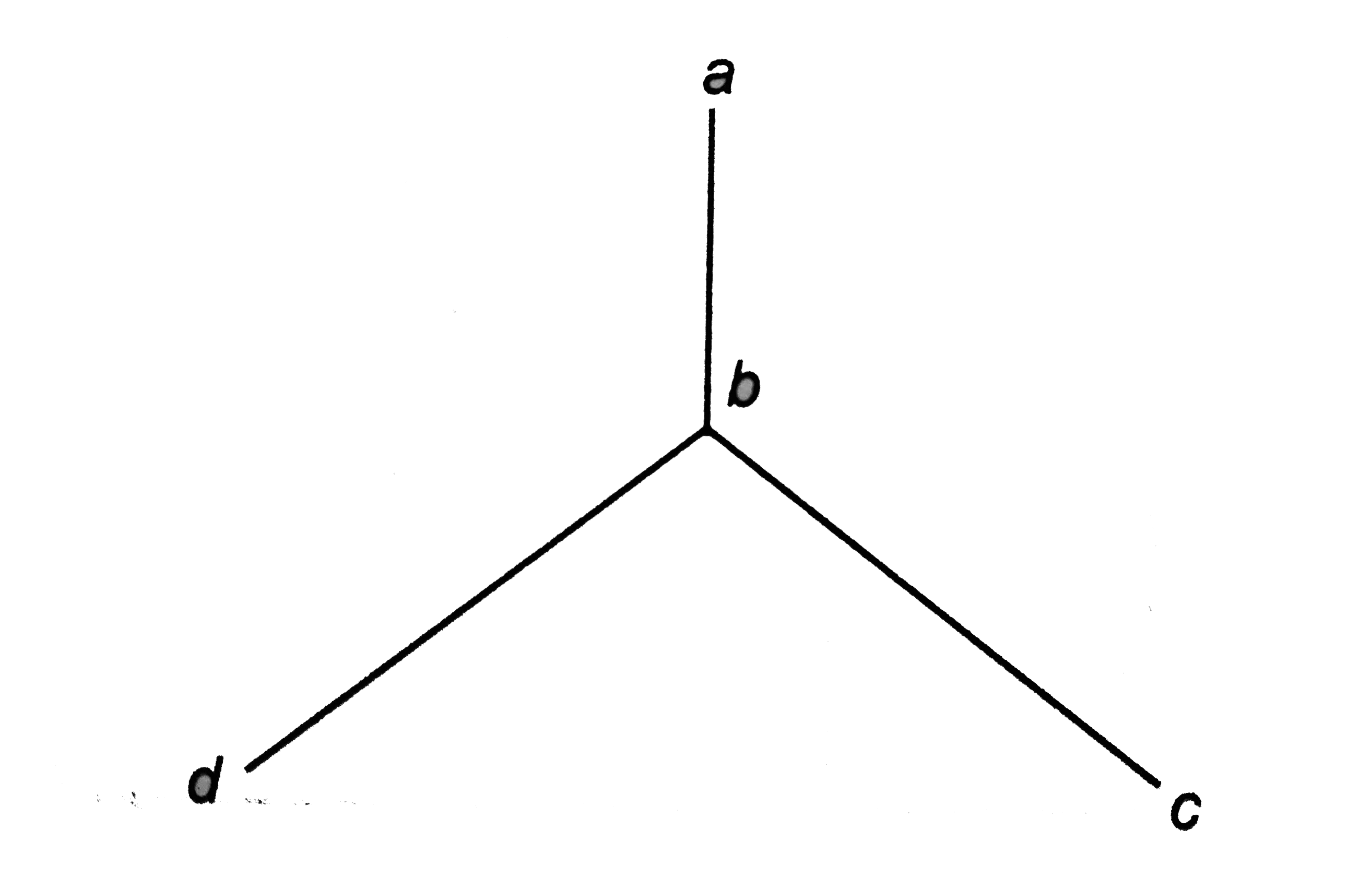 Atemperature of junction b is 15∘C.Btemperature of junction b is 30∘CCheat will flow from b to dDboth (b) and (c)
Atemperature of junction b is 15∘C.Btemperature of junction b is 30∘CCheat will flow from b to dDboth (b) and (c)A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22))
A spring of force constant k is cut into two pieces of lengths l1 and l2. Calculate force constant of each part.
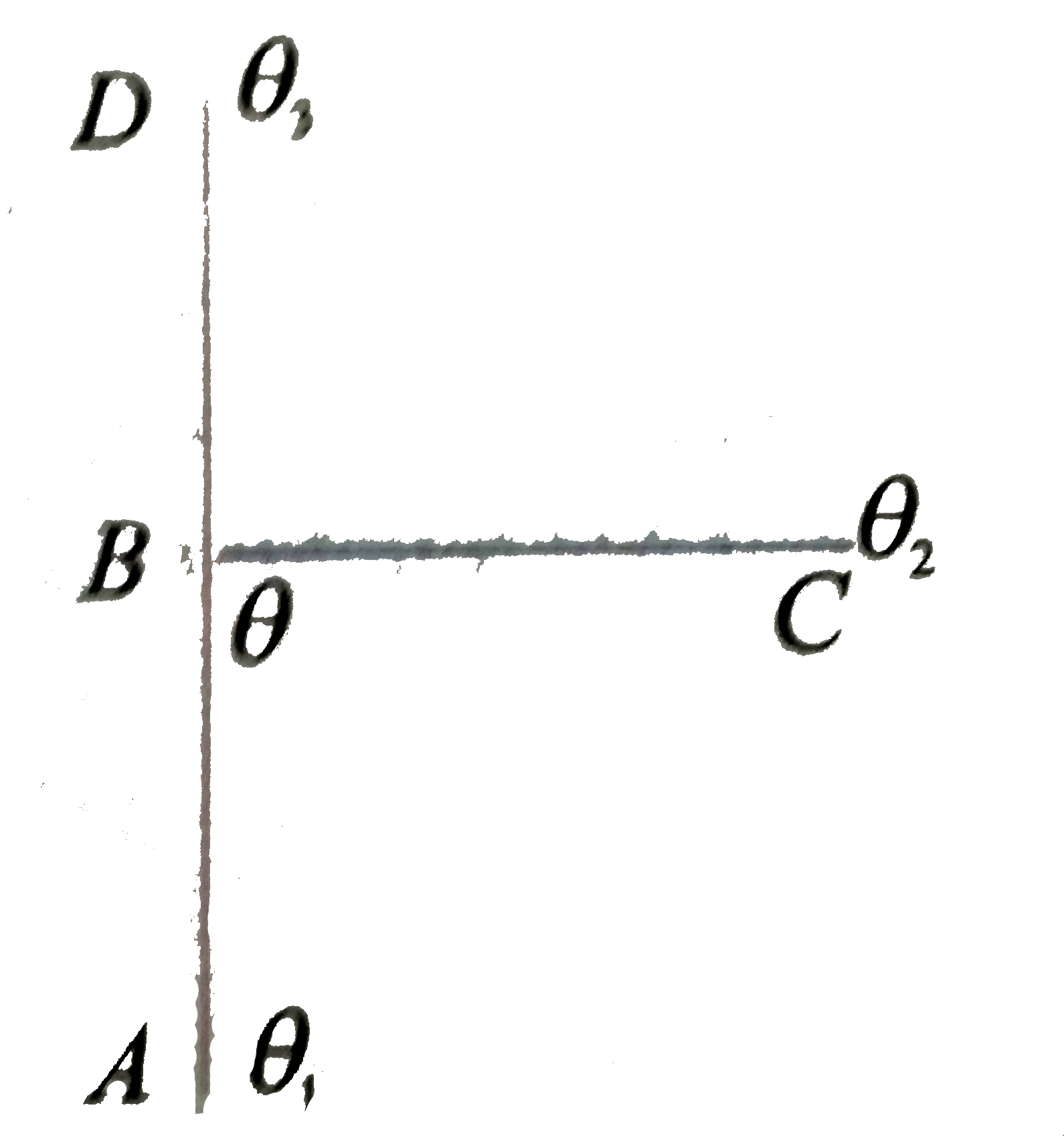
View SolutionThree rods AB,BCand BD having thremal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in The ends A,C and D are at temperature θ1,θ2 and θ3 respectively Find the temperature of the junction B
(Assume steady state and θ1>θ>θ2>θ3)
 .
.
View SolutionThe base of a triangle is divided into three equal parts. If θ1,θ2,θ3 be thw angles subtended by these parts at the vertex, then prove that
(cotθ1+cotθ2)(cotθ2+cotθ3)=4cosec2θ2
View SolutionIf a magnet of pole strength m is divided into four parts such that the length and width of each part is half that of initial one, then the pole strength of each part will be
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
View Solution