The figure shows an insulated cylinder divided into three parts A,B and C. Pistons I and II are connected by a rigid rod and can move without friction inside the cylinder. Piston I is perfectly conducting while piston II is perfectly insulating. The initial state of the gas (γ=1.5) present in each compartment A,B and C is as shown. Now , compartment A is slowly given heat through a heater H such that the final volume of C becomes 4V09. Assume the gas to be ideal and find.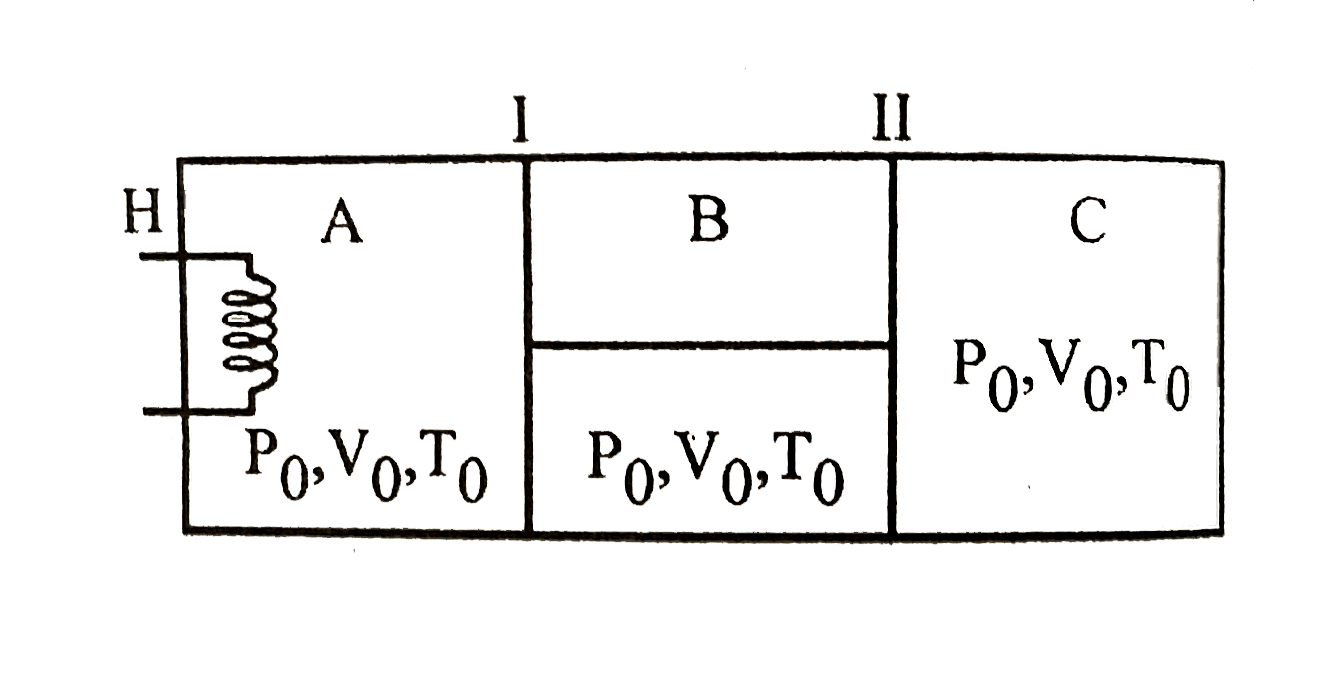
Final pressures in each compartment A,B and C
Final temperatures in each compartment A,B and C
Heat supplied by the heater
Work done by gas in Aand B
Heat flowing across piston I.
The correct Answer is:(a)finla pressure in A=278P0=Final pressure in C, finla pressure in B=214P0
(b)finla temperature in (AandB)=214t0,finla temperature in C=32T0,
(c) 18P0V0,
(d)Work done by gas in A=+P0V0Work done by gas in B=0,
(e)172P0V0
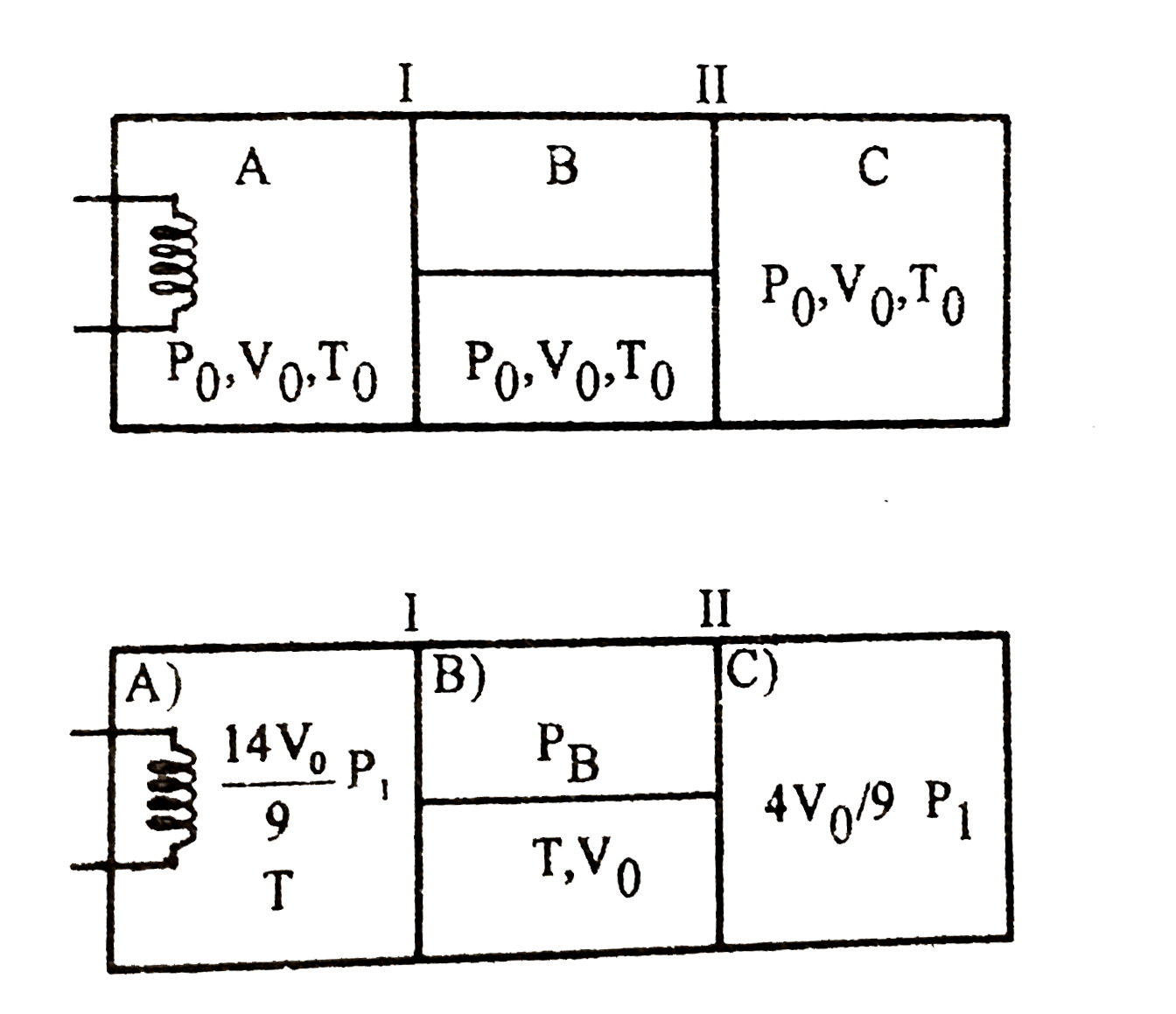

(a)For compartment -C
PVr=constant
P0V320=P1(4V09)32
P1=P0(94)32=27p08
P1= Final pressure in A = finla pressure in c as movable pistion is in equilibrium Temperature in compartment A
P0V0T0=P1(14V09)T0⇒P0V0T0=(278)P0×(149)V0T
Temperature in A = Temperture in B(as conducting) For C
P0V0T0=4V09×27P08Tc
Tc=4×279×8T0=32T0
pressure in 'B' = P_(B)<br>Then
PBT=P0T0⇒PB=P0TT0=214T0P0T0=214P0
Heat supplical by heat r =Qb
△Qb=nCv△(T)=f2(nRT2−nRT1)
=f2(V0)(PB−P0)
f2V0(174P0)
=17fP0V08 ltbRgt r=1.5⇒f=4
Q△b=172P0V0
ForA"
PA=Pc
VA=W0−Vc
dVA=dVc
WA=∫PAdVA−∫PcdVc
=−Wc
=[PiVi−PfVFR1]
=[Pfc−PicVicr1]
WA=4V09×27P08−P0V01/2
=P0v01/2=P0V0
△UA=f2(nR△TA)=(P1×14V09−P0V0)f2
=(278P0×14V09−P0V0)f2
(214P0V0−P0v0)f2
=(174P0V0)×2
=△Q=174P0V0+172P0v0
=18P0V0
Wa=P0V0
Heatflow=△Qb=172P0V0
Topper's Solved these Questions
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Exercise-4
Explore 35 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Section-B
Explore 13 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Matrix Type
Explore 2 Videos
- HEAT TRANSFERBook:BANSALChapter:HEAT TRANSFERExercise:Exercise
Explore 89 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:Exercise
Explore 10 Videos
Similar Questions
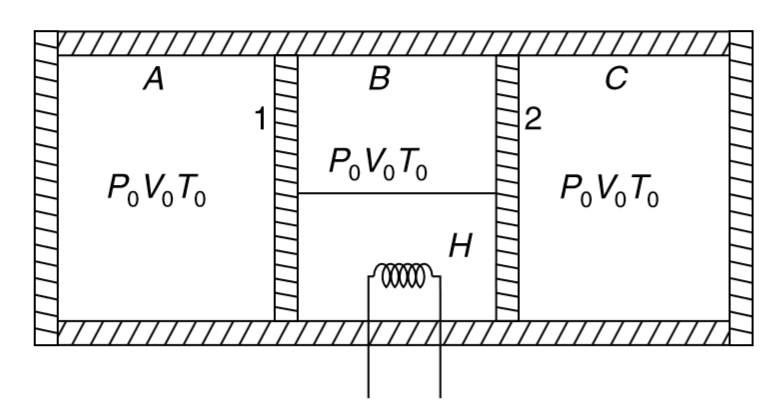
An insulated cylinder is divided into three parts A, B and C. Pistons 1 and 2 are connected by a rigid rod and can slide without friction inside the cylinder. Piston 1 is perfectly conducting while piston 2 is perfectly insulating. Equal quantity of an ideal gas is filled in three compartments and the state of gas in every part is same (P0V0T0). Adiabatic exponent of the gas is g = 1.5. The compartment B is slowly given heat through a heater H such that the final volume of gas in part C becomes 4V09
(a) Calculate the heat supplied by the heater.
(b) Calculate the amount of heat flow through piston 1.
(c) If heater were in compartment A, instead of B how would your answers to (a) and (b) change?
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final presssures of left and right compartment respectively are
View Solution
Knowledge Check
A gas is filled in the cylinder shown in fig. The two pistons are joined by a string. If the gas is heated, the right piston will
 Amove toward leftBmove toward rightCremain stationaryDnone of these
Amove toward leftBmove toward rightCremain stationaryDnone of theseThe piston I s now pulled out slowly and held at a diatance 2L from the top. The pressure in the cylinder between its top and the piston will then be
AP0BP0/2CP02+MgϕR2DP02−Mgϕr2Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.AV2(P1T2P2T1+P1T2)BV(P1T2P2T1−P1T2)CV(P1T2P2T1+P1T2)DV(2P1T2P2T1+P1T2)
Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final temperature
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final pressures of left and right compartment respectively are
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of right compartment.
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final temperature
View Solution

