A heat-conducting piston can freely move inside a closed thermally insulated cylinder with an ideal gas. In equilibrium the piston divides the cylinder into two equal parts, the gas temperature being equal to T0. The piston is slowly displaced. Find the gas temperature as a function of the ratio η of the volumes of the greater and smaller sections. The adiabatic exponent of the gas is equal to γ.
The correct Answer is:T0[(n+1)24n]γ−12
Let d be the distance through Which the piston has to be moved to male the volume of one part n times that of the other part. Then
n =V0+AdV0−Ad or d=n−1n+1×V0A
Now consider any displacement of the piston by x. Since the pistionis conducting and the process of compressionis slow, the temperature of gases on the two sides of the piston will be the same."
∴p0v0T0=p1(V0+Ax)T=P2(V0−Ax)T
Since it is a quasi static process
p1A+Fagent=p2AorFagent=(P2−P1)A
Then dW, elementary work done by agent =Fa≥ntdx=(P2−p1)Adx
or dW=mMRT(1V0−Ax−1V0+Ax)Adx
=mMRT2A2xdxV20−A2x2
Now dU=2mMCvdT
By 1st law of thermodynamics dQ=dU+dW
Here dQ=0∴dU=−dW
or 2mMCvdT=mMRT2A2xdxV20−A2x2
or Rγ−1dT=RTA2xdxV20−A2x2 or 1γ−1T∫T0dTT=A2d∫0xdxV20−A2x2
or1γ−1InTT0=A2d∫0xdxV20−A2x2
Put(V20−A2x2)=z. Then-(2A2xdx)=dz
∴∫xdxV20−A2x2=∫−12A2dzz=−12A2Inz=12A2In(V20−A2x2)
∴1γ−1∈TT0=A2×−12A2[In(V20−A2x2)]d0
=12[In(V20−A2dd)−InV20]
=−12[In(1−A2V20.(n−1)2V20(n+1)2A2)]=12In4n(n+1)2
or InTT0=−γ−12In4n(n+1)2
or T=T0[(n+1)24n]γ−12
Topper's Solved these Questions
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Exercise-4
Explore 35 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Section-B
Explore 13 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Matrix Type
Explore 2 Videos
- HEAT TRANSFERBook:BANSALChapter:HEAT TRANSFERExercise:Exercise
Explore 89 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:Exercise
Explore 10 Videos
Similar Questions
A heat conducting piston can move freely inside a closed thermally isolated cylinder which contains an ideal gas. In equilibrium the piston divides the cylinder in two equal parts, the temperature of the gas being T0. The piston is slowly displaced. Find the temperature of the gas when the volume of one part is n times greater than that of the other part. The adiabatic exponent of the gas is γ.
View SolutionA heat conducting piston can move freely inside a closed, thermally insulated cylinder with an ideal gas (γ= 5/3). At equilibrium, the piston divides the cylinder into two equal parts, the gas temperature being equal to 300 K. The piston is slowly displaced by an external agent. Find the gas temperature when the volume of the greater section is seven times the volume of the smaller section.
View Solution
Knowledge Check
A closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
If the piston is slightly displaced by x, the net force acting on the piston isAP0γA2xV0B2P0γA2xV0C3P0γA2xV0DP0γA2x(γ−1)V0A closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
The time period of oscillation for small displacements of the piston isA2π√mV02P0γA2B2π√mV04P0γA2C2π√mV0(γ−1)2P0γA2Dnone of these
(i) A conducting piston divides a closed thermally insulated cylinder into two equal parts. The piston can slide inside the cylinder without friction. The two parts of the cylinder contain equal number of moles of an ideal gas at temperature T0. An external agent slowly moves the piston so as to increase the volume of one part and decrease that of the other. Write the gas temperature as a function of ratio (β) of the volumes of the larger and the smaller parts. The adiabatic exponent of the gas is γ.
(ii) In a closed container of volume V there is a mixture of oxygen and helium gases. The total mass of gas in the container is m gram. When Q amount of heat is added to the gas mixture its temperature rises by ΔT. Calculate change in pressure of the gas.
View SolutionIn a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass m and cross − sectional area S (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime V0 . The gas ppressure is p0. The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.
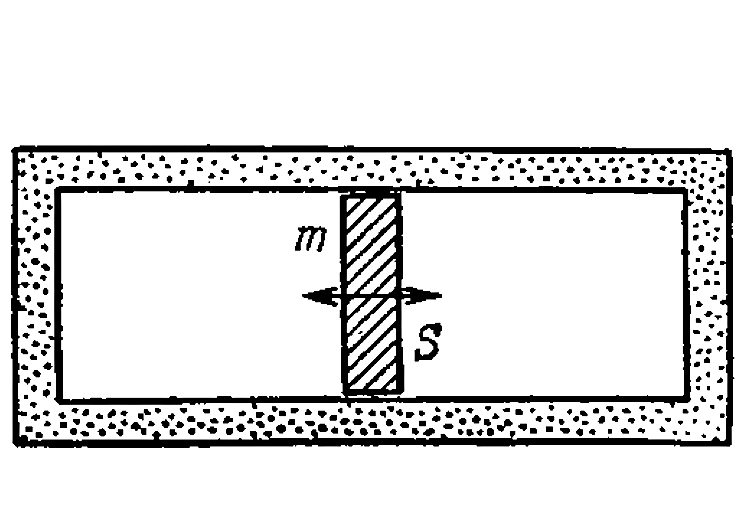
View SolutionA piston can freely move inside a horizontal cylinder closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts each of volmek V0 in which an ideal gas is contained under the same pressure p0 and at the same temperature. What work has to be performed in order to increase isothermally the volume of one part of gas η times compared to that of the other by slowly moving the piston ?
View SolutionA weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and entropy of the gas was resulting from these two processes.
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View SolutionOne mole of an ideal gas is contained in a vertical cylinder under a massless piston moving without friction. The piston is slowly raised so that the gas expands isothermally at temperature T0 = 300 K. Find the amount of work done increasing the volume to η=2 times. The outside pressure is atmospheric.
View Solution

