The area bounded by the
curve y=x|x|
, x-axis and the ordinates x=1 is given by
[Hint : y=x2
if x > 0
and y=−x2
if x < 0
].
A
0
B
13
C
23
D
43
Video Solution
Text Solution
The correct Answer is:C
Given, y=x|x|={ x2,x≥0−x2,x<0
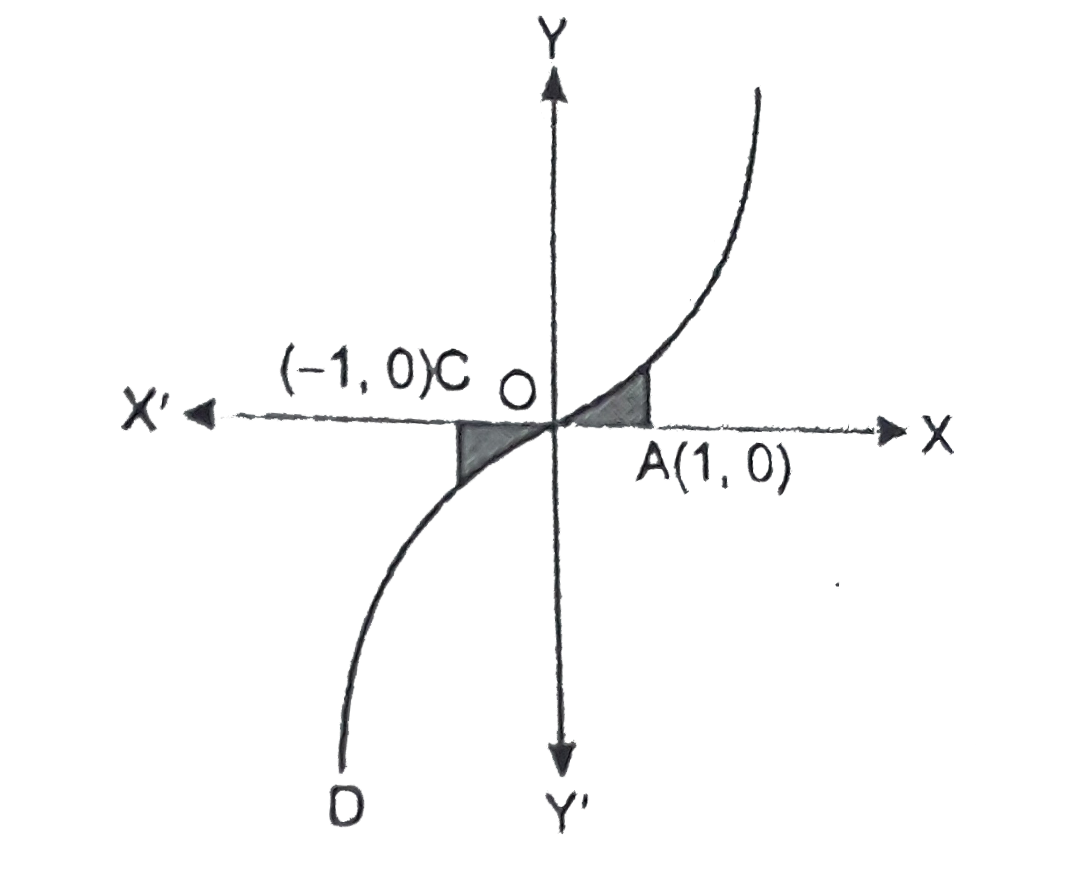
∴ Required area =2∫10x|x|=2∫10x2dx
=2[x33](0)1=23(13−03)
=23 sq. unit.
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8.2
Explore 7 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- Continuity and DifferentiabilityBook:NAGEEN PRAKASHANChapter:Continuity and DifferentiabilityExercise:Miscellaneous Exercise
Explore 23 Videos
Similar Questions
Knowledge Check
The area bounded by the curve y = log x, X- axis and the ordinates x = 1, x = 2 is
Alog 4 sq. unitsBlog 2 sq. unitsC(log 4 - 1) sq. unitsD(log 4 + 1 ) sq. unitsThe area bounded by the curve y=x|x|, x-axis and the ordinates x=1,x=-1 is given by
A0B1/3C2/3D1The area bounded by the curve y=x|x|, x-axis and the ordinates x=1,x=-1 is given by
A0B13C23D43
Find the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionArea bounded by the curve y=x3, the x-axis and the ordinates x=−2andx=1 is
View SolutionArea bounded by the curve y=x2, the x-axis and the ordinates x=−2andx=1 is :
View SolutionThe area bounded by the curve y=x(x2−1) and x-axis is
View SolutionThe area bounded by the curve y=(x−1)(x−2)(x−3), x-axis and ordinates x=0,x=3 is :
View Solution

