The area (in square units) bounded by the curve $y = x^{3}$ , the x-axis and the ordinates at $x = - 2 and x = 1$ is

A

$- 9$

B

$\frac{- 15}{4}$

C

$\frac{15}{4}$

D

$\frac{17}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given curve is $y = x^{3}$
If we replace x by -x and y by -y then we get $y = x^{3}$ .
Therefore, curve is symmetric in opposite quadrants and passes through the orgin (0, 0).

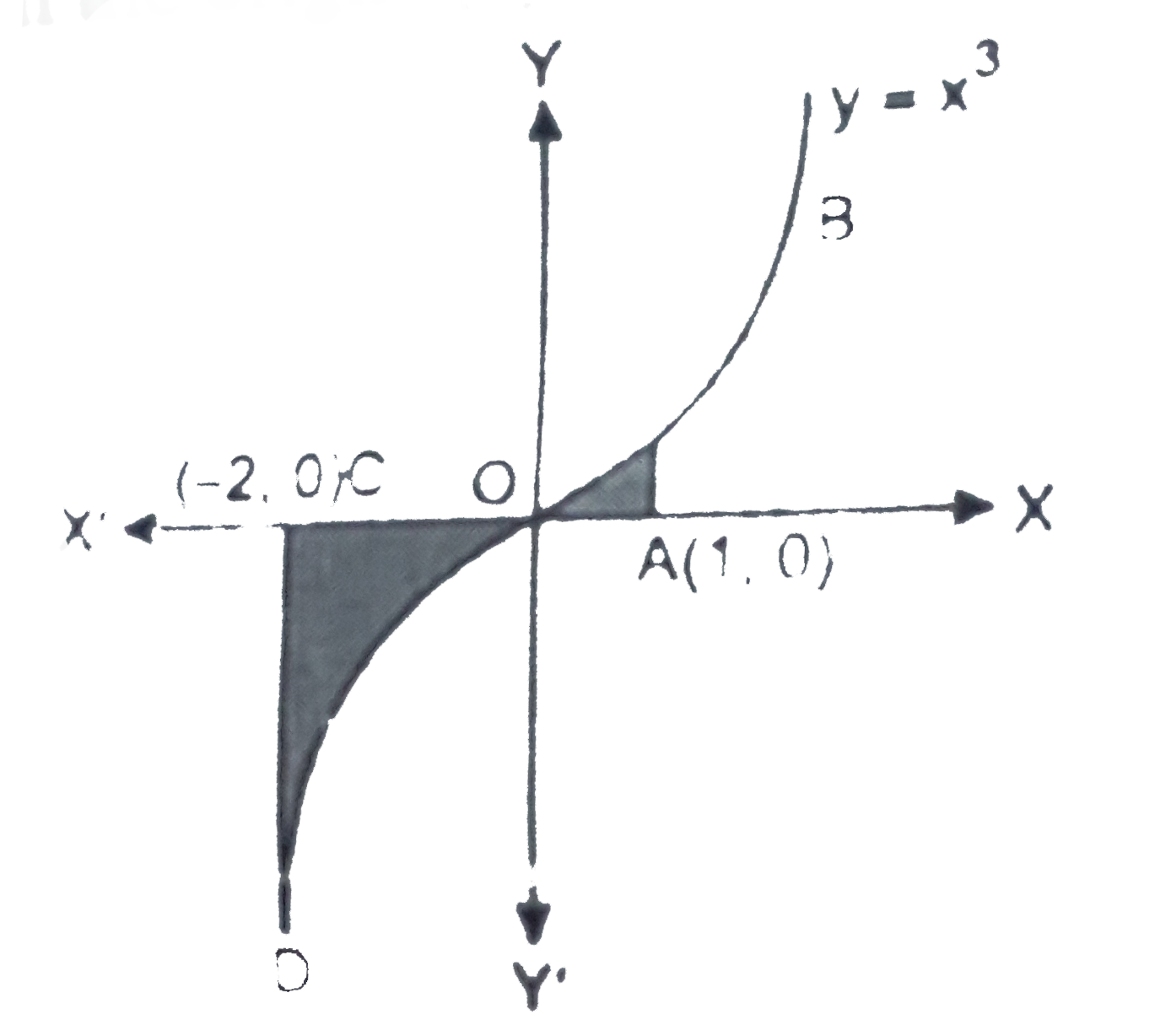
$∴$ Required area $= \int_{- 2}^{1} ∣ ∣ x^{3} ∣ ∣ d x$
$= \int_{- 2}^{0} ∣ ∣ x^{3} ∣ ∣ d x + \int_{0}^{1} ∣ ∣ x^{3} ∣ ∣ d x$
$= \int_{- 2}^{0} (- x^{3}) d x + \int_{0}^{1} x^{3} d x$
$= - {[\frac{x^{4}}{4}]}_{- 2}^{0} + {[\frac{x^{4}}{4}]}_{0}^{1}$
$= - [0 - \frac{{(- 2)}^{4}}{4}] + [\frac{1}{4} - 0]$
$= - (- 4) + (\frac{1}{4}) = \frac{17}{4}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Area bounded by the curve $y = x^{3}$ , the x-axis and the ordinates $x = - 2 and x = 1$ is
A-9
B $- \frac{15}{4}$
C $\frac{15}{4}$
D $\frac{17}{4}$
Question 2 - Select One
Area bounded by the curve $y = x^{2},$ the x-axis and the ordinates $x = - 2 and x = 1$ is :
A $- 9$
B $- \frac{15}{4}$
C $\frac{15}{4}$
D $\frac{17}{4}$
Question 3 - Select One
The area in square units bounded by the curves $y = x^{3}, y = x^{2}$ and the ordinates $x = 1, x = 2$ is
A $17 / 12$
B $12 / 13$
C $2 / 7$
D $7 / 2$

NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise

Home
Ask Doubt
Profile