Find the area enclosed between the parabola $y^{2} = 4 a x$ and the line $y = m x$ .

Video Solution

Text Solution

Verified by Experts

Given, curve $y^{2} = 4 a x$ …(1)
and equation of line, $y = m x$ …(2)

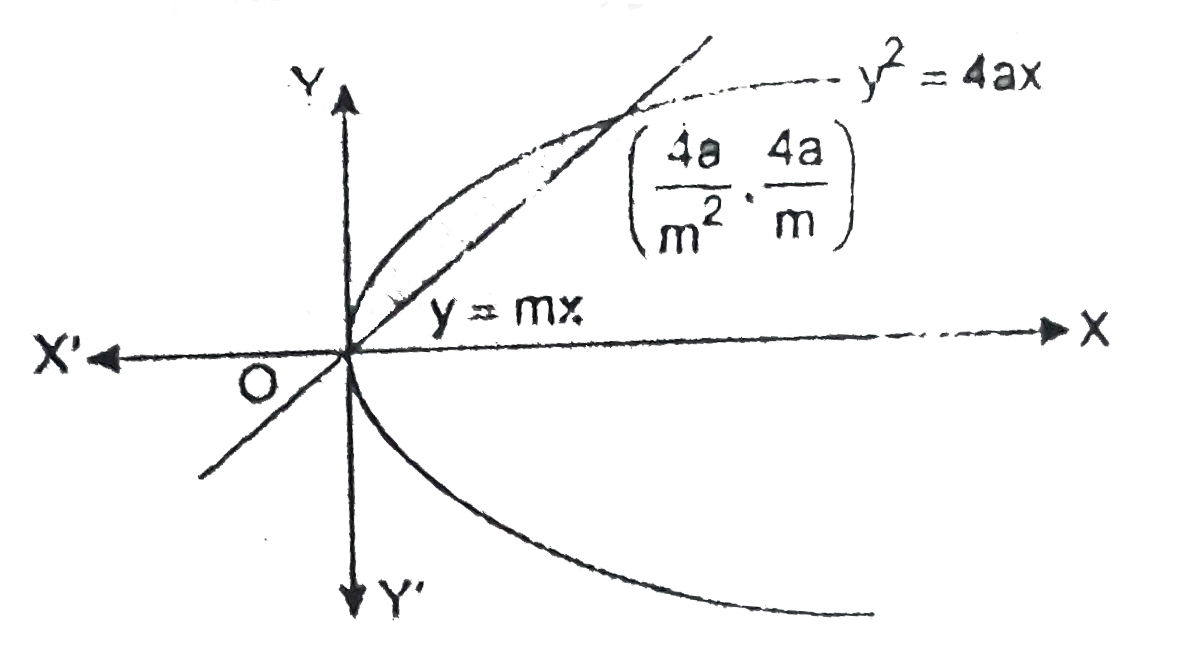
From equations (1) and (2),
${(m x)}^{2} = 4 a ξ m p l i e s x (m^{2} x - 4 a) = 0$
$\Rightarrow x = 0 or x = \frac{4 a}{m^{2}}$
When, $x = 0, y = m \times 0 = 0$
When, $x = \frac{4 a}{m^{2}}, y = m \times \frac{4 a}{m^{2}} = \frac{4 a}{m}$
$∴$ The points of intersection of two curves are (0, 0) and $(\frac{4 a}{m^{2}}, \frac{4 a}{m}) .$
$∴$ Required area $\int_{0}^{4 a / m^{2}} (\sqrt{4 a x} - m x) d x$
$= 2 \sqrt{a} {[\frac{x^{3 / 2}}{3 / 2}]}_{0}^{4 a / m^{2}} - {[m \cdot \frac{x^{2}}{2}]}_{0}^{4 a / m^{2}}$
$= \frac{4}{3} \sqrt{a} {(\frac{4 a}{m^{2}})}^{3 / 2} - \frac{m}{2} {(\frac{4 a}{m^{2}})}^{2}$
$= \frac{4}{3} \sqrt{a} \cdot (\frac{4 a}{m^{2}}) \sqrt{\frac{4 a}{m^{2}}} - \frac{m (16 a^{2})}{2 m^{4}}$
$= \frac{32}{3} \cdot \frac{a^{2}}{m^{3}} - \frac{8 a^{2}}{m^{3}}$
$= \frac{8 a^{2}}{3 m^{3}}$ sq. units.

Updated on:21/07/2023