A cylindrical tank contains water up to a height H. If the tank is accelerated upwards with acceleration a, the pressure at the A is p1. If the tank is accelerated downwards with acceleration a the pressure at A is p2. Then
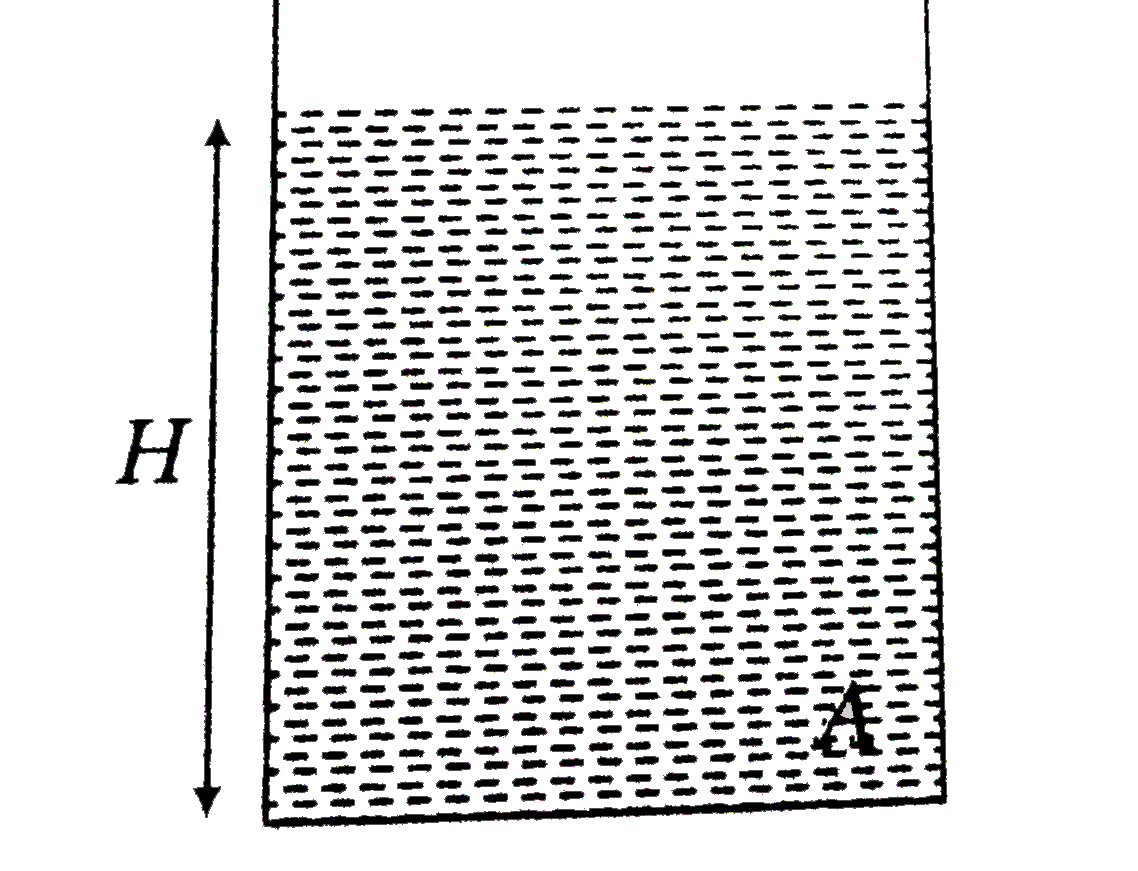
p1<p2
p1=p2
p1>p2
Data insufficient
The correct Answer is:C
When moving upwards dpdh=−ρ(g+a) and when moving downwards dpdh=−ρ(g−a)
In first case, pressure decreases with h more repidly.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
An open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.

View SolutionA water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View Solution
Knowledge Check
An open cylindrical tank is of radius 2.8 m and height 3.5 m. What is the capacity of the tank?
A96.24 m3B84.26 m3C86.24 m3D82.64 m3If a vessel containing a fluid of density ρ upto height h is accelerated vertically downwards with accelerations a0. Then the pressure by fluid at the bottom of a vessel is
Ap=p0+ρgh+ρha0Bp=p0+ρghCp=p0+ρh(g−a0)Dp=p0ρghA closed rectangular tank is completely filled with water and is accelerated horizontally with an acceleration towards the righ. Pressure is i. maximum and ii. minimum at
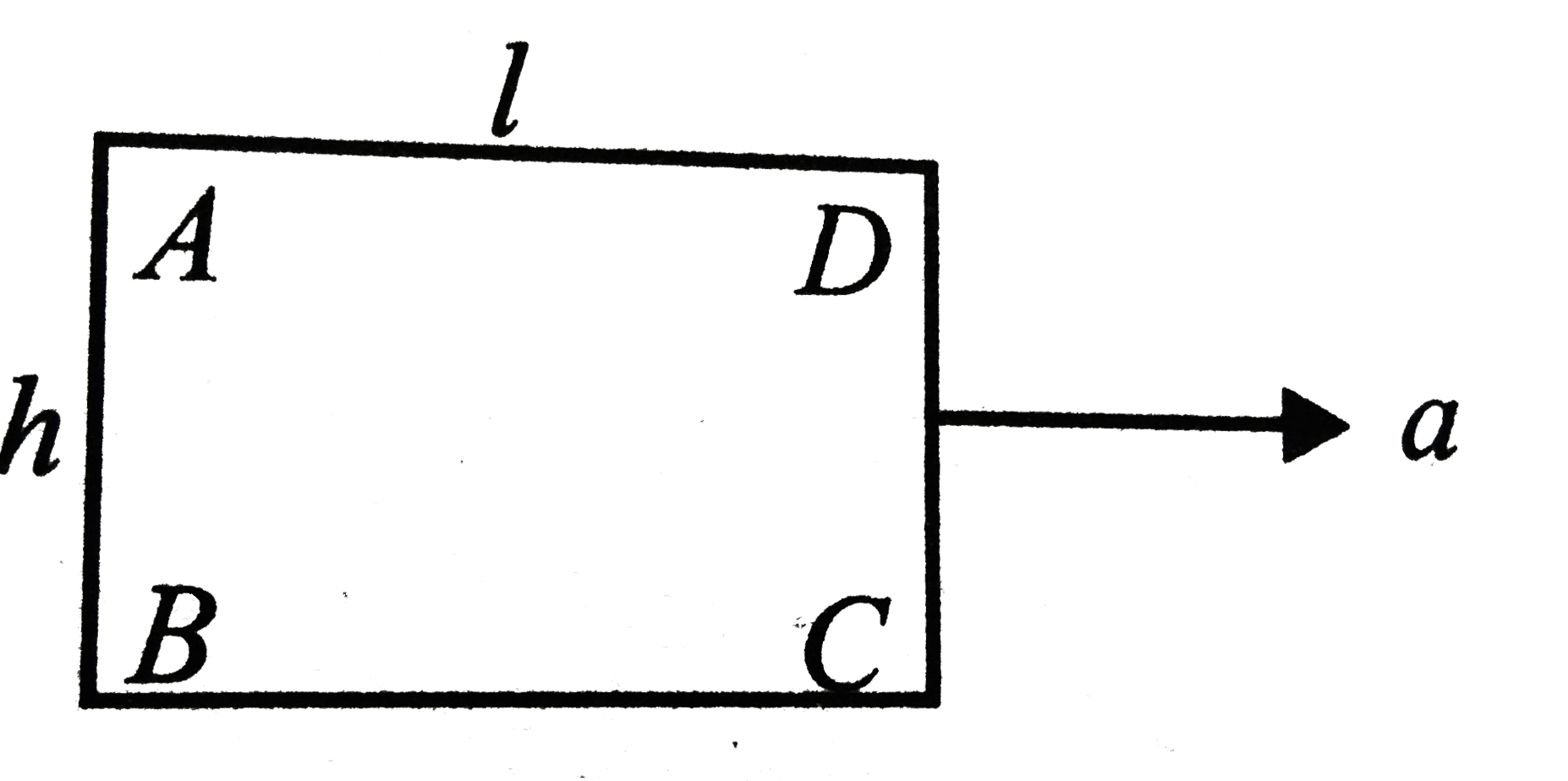 Ai. B ii DBi C ii DCi B ii CDi B ii A
Ai. B ii DBi C ii DCi B ii CDi B ii A
A stationary vertical cylindrical container of very large height filled with a gas of molar mass M at constant Temperature. The pressure at the bottom is P1 and at the top is P2. If the acceleration due to gravity is assumed to be constant for the whole cylinder, which is equal to g. Then the height of the cylinder is :
View SolutionA completely filled cylinderical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time t0 such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time?
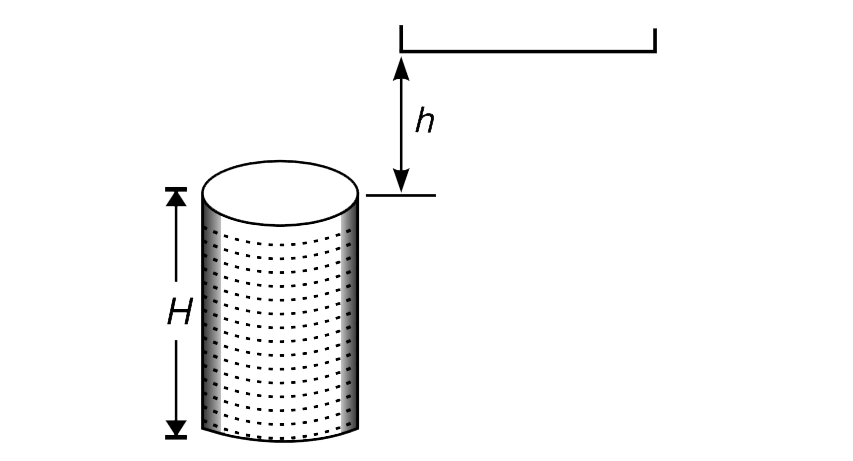
View SolutionWater rises to a height h1 in a capillary tube in a stationary lift. If the lift moves up with uniform acceleration it rises to a height h2, then acceleration of the lift is
View SolutionThe pulley in the diagram are all smooth and light. The acceleration of A is a upwards and the acce,leration of C is f downwards. The acceleration of B is
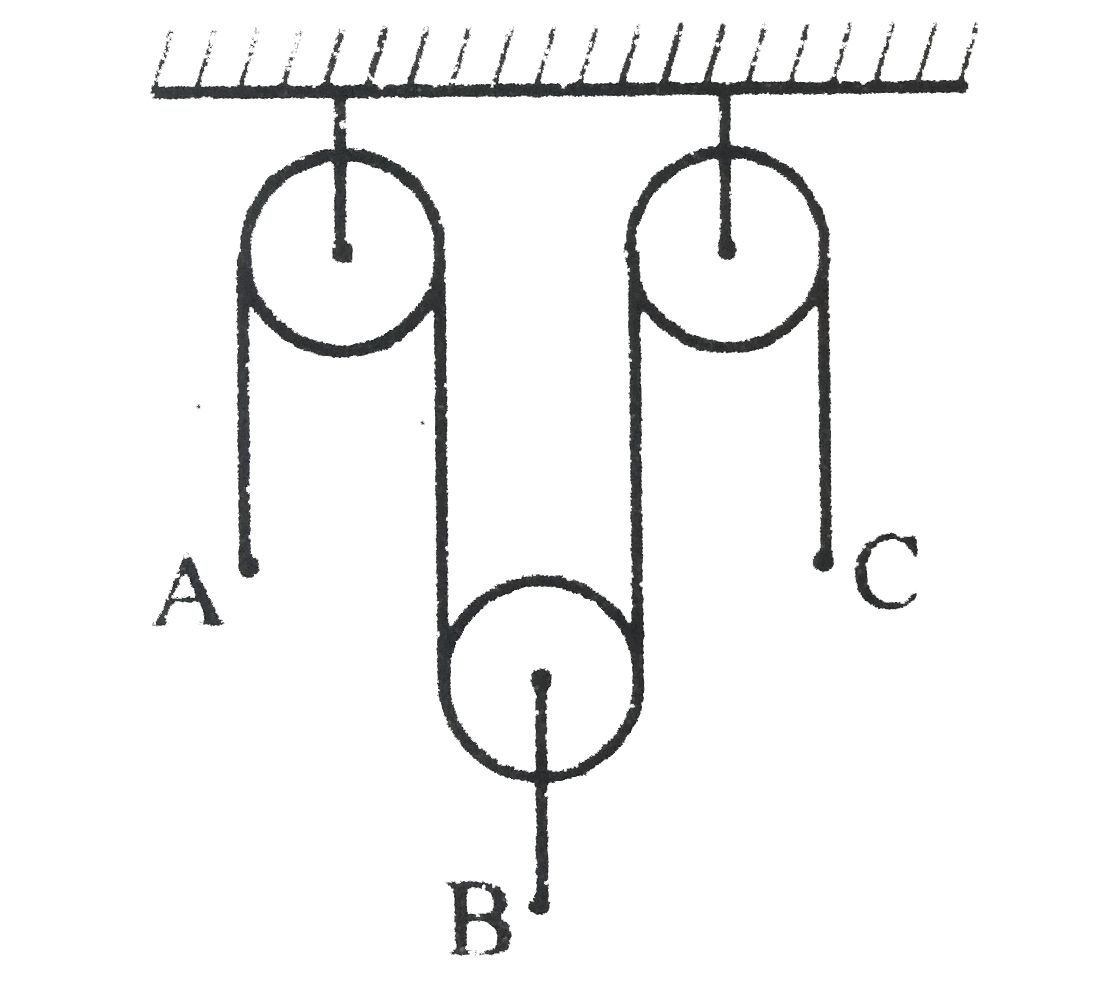
View SolutionA block is partially immeresed in a liquid and the vessel is accelerating upwards with an acceleration 'a'. The block is observed by two observers O1 and O2, one at rest and the other accelerating with an acceleration 'a' upward. The total buoyant force on the block is :
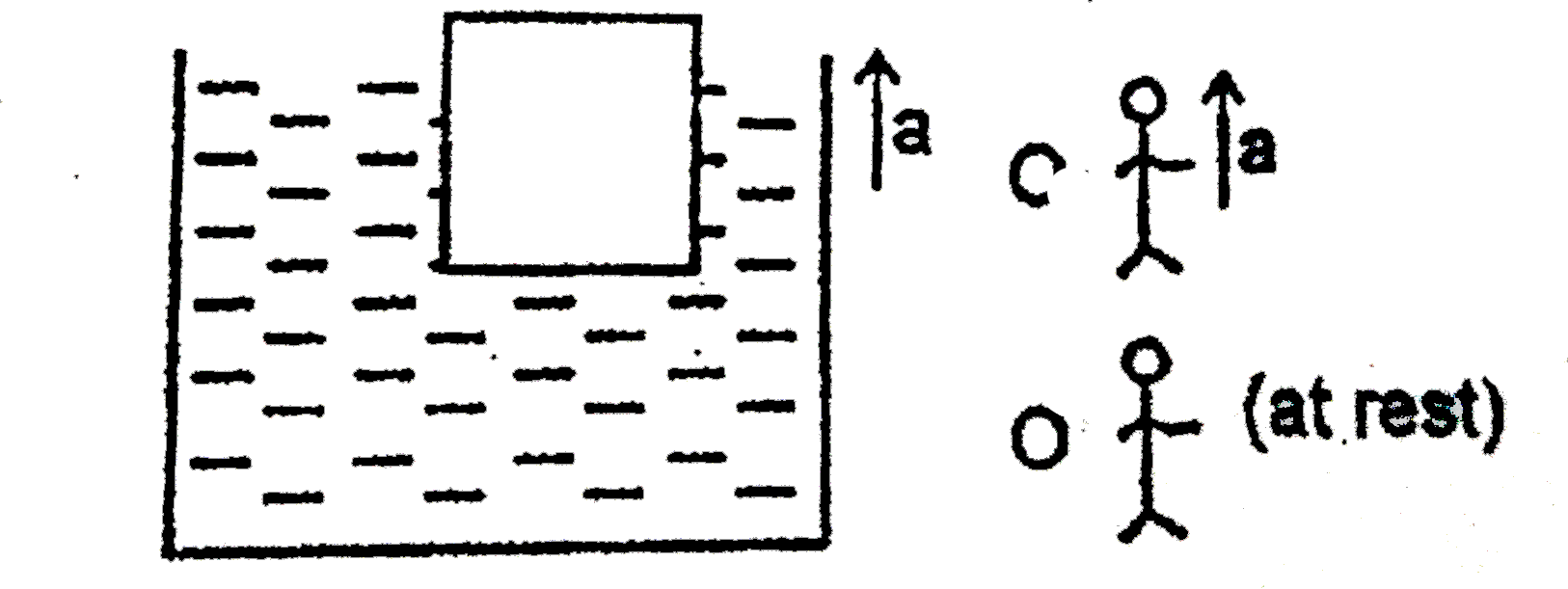
View Solution
