Two identical cylindrical vessel with their bases at the same level each contain a liquid of density $ρ$ . The height of the liquid in one vessel is $h_{1}$ and in the other is $h_{2}$ the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?

A

$2 ρ A {g (h_{2} - h_{1})}^{2}$

B

$ρ A {g (h_{2} - h_{1})}^{2}$

C

$\frac{1}{2} ρ A {g (h_{2} - h_{1})}^{2}$

D

$\frac{1}{4} ρ A {g (h_{2} - h_{1})}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Common height after they are connected can be determined by equating the volume. Hence
$(A_{1} + A_{2}) h = A_{1} h_{1} + A_{2} h_{2} (A_{1} = A_{2} = A)$
$∴ h = \frac{h_{1} + h_{2}}{2}$
Work done by gravity $= - Δ U = U_{i} - U_{f}$
$= {A h_{1} ρ . g . \frac{h_{1}}{2} + A h_{2} ρ . g . \frac{h_{2}}{2}} - A (h_{1} + h_{2}) ρ . g . \frac{(h_{1} + h_{2})}{4}$
$= \frac{ρ A g}{4} {(h_{2} - h_{1})}_{2}^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density $ρ$ . The area of either base is A but in one vessel the liquid height is $h_{1}$ and in the other liquid height is $h_{2} (h_{2} < h_{1})$ . If the two vessel are connected, the work done by gravity in equalizing the level is
A $\frac{1}{2} {(h_{1} - h_{2})}_{1}^{2} A ρ g$
B $\frac{1}{2} {(h_{1} + h_{2})}_{1}^{2} A ρ g$
C $\frac{1}{2} {(h_{1}^{2} - h_{2}^{2})}^{2} A ρ g$
D $\frac{1}{4} {(h_{1} - h_{2})}_{1}^{2} A ρ g$
Question 2 - Select One
A liquid of density $ρ$ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is $h_{1}$ and that in the other vessel is $h_{2}$ . If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
A $(h_{1} - h_{2}) g ρ$
B $(h_{1} - h_{2}) g A ρ$
C $\frac{1}{2} {(h_{1} - h_{2})}_{1}^{2} g A ρ$
D $\frac{1}{4} {(h_{1} - h_{2})}_{1}^{2} g A ρ$
Question 3 - Select One
A U-tube of cross section A and 2A contains liquid of density $ρ$ . Initially, the liquid in the two arms are held with a level difference h as shown in figure. After being released the levels equalize after some time. The work done by gravity forces on the liquid in the process is :

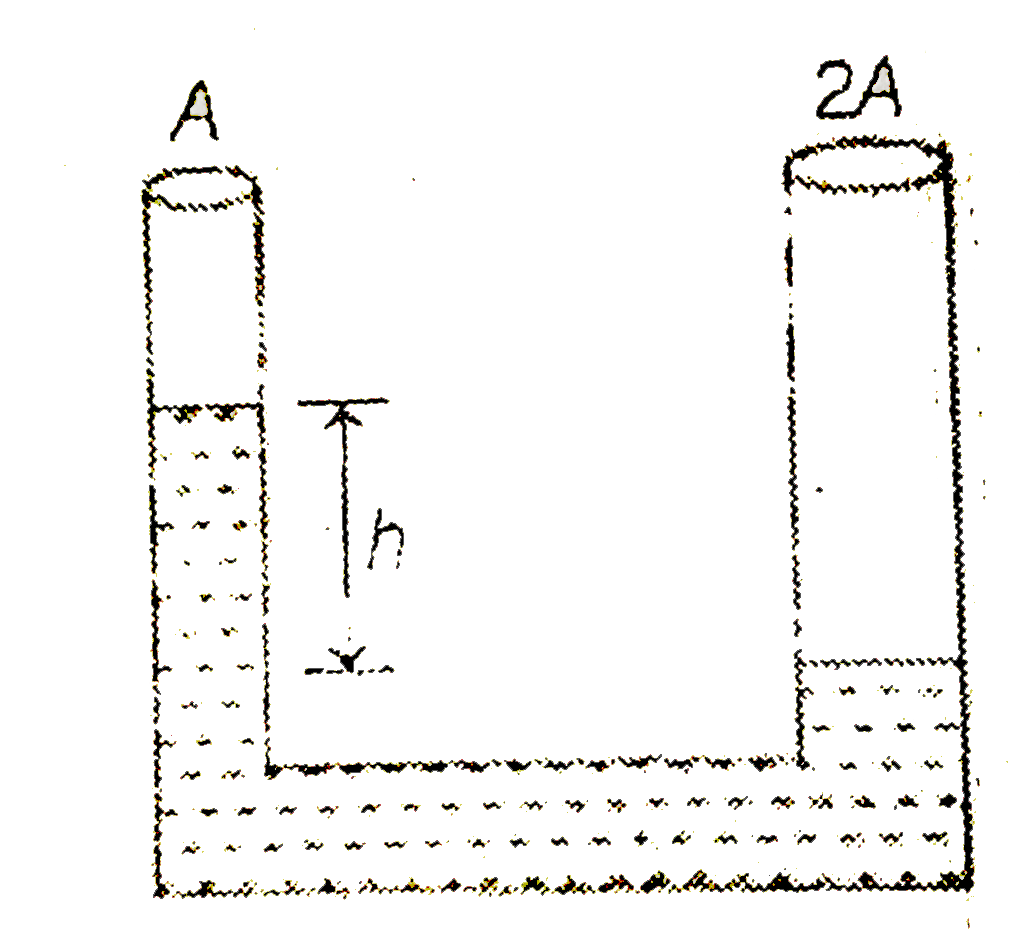A $\frac{2}{3} ρ A g h^{2}$
B $ρ A g h^{2} / 3$
C $ρ A g h^{2} / 6$
D $\frac{3}{4} ρ A g h^{2}$

DC PANDEY-FLUID MECHANICS-Taking it together

Home
Ask Doubt
Profile