A container has a small hole at its bottom. Area of cross-section of the hole is A1 and that of the container is A2. Liquid is poured in the container at a constant rate Qm3s−1. The maximum level of liquid in the container will be
Q22gA1A2
Q22gA21
Q2gA1A2
Q22gA2^(2)
The correct Answer is:B
Level in the container will become maximum when rate of inflow = rate of outflow.
Q=A1v=A1√2ghmax
∴ hmax=Q22gA21
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cylindrical container has a cross sectional area of A0=1cm2 at 0∘C. A scale has been marked on vertical surface of the container which shows correct reading at 0∘C. A liquid is poured in the container. When the liquid and container is heated to 100∘C, the scale shows the height of the liquid as 83.33 cm. The coefficient of volume expansion for the liquid is γ=0.001∘C−1 and the coefficient of linear expansion of the material of cylindrical container is α=0.0005∘C−1. A beaker has 300cm3 of same liquid at 0∘C. The two liquids are mixed. Find the final temperature of the mixture assuming that heat exchange takes place between the liquids only, and its specific heat capacity is independent of temperature
View SolutionA pressure exerted by mercury at the bottom of a container of area of cross section 2cm2 is 10 Pa. Determine the weight of the mercury in the container.
View Solution
Knowledge Check
A stone is placed inside a container. The normal reaction between the stone and the container is N1. Now a liquid is poured inside the container such that normal reaction between stone and the container is N2 then
(Assume no liquid between stone and container at the contact surface)AN2<N1BN2>N1CN2=N1DNone of theseIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
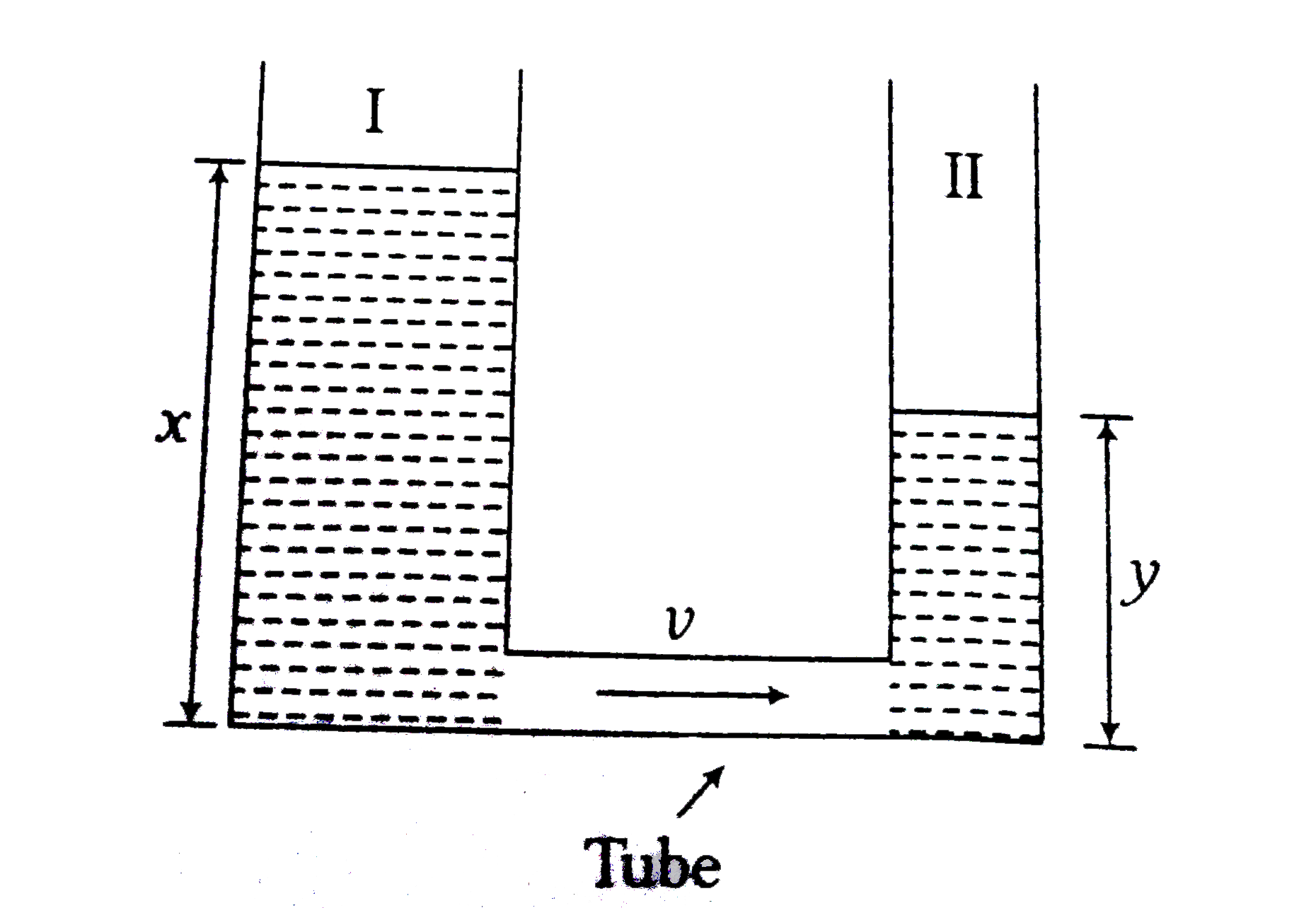 A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of these
A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of theseOn heating a liquid of coefficient of cubical expansion γ in a container having coefficient of linear expansion γ/3. The level of liquid in the container will
AriseBfallCwill remain almost stationaryDit is difficult to say
A pressure exerted by mercury at the bottom of a container of area of cross section 2cm2 is 10 Pa. Determine the weight of the mercury in the container.
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
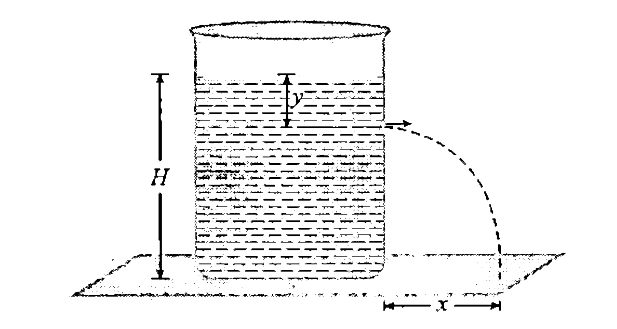
View SolutionFrom a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.

View SolutionA container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case

View SolutionA hollow cylindrical container floats in water with half its length immersed. A liquid of specific gravity σ is slowly poured into the container until the levels of the liquid inside the container and of water outside are the same. It is observed that the container is submerged to two-thirds its length. Then the value of σ is
View Solution
