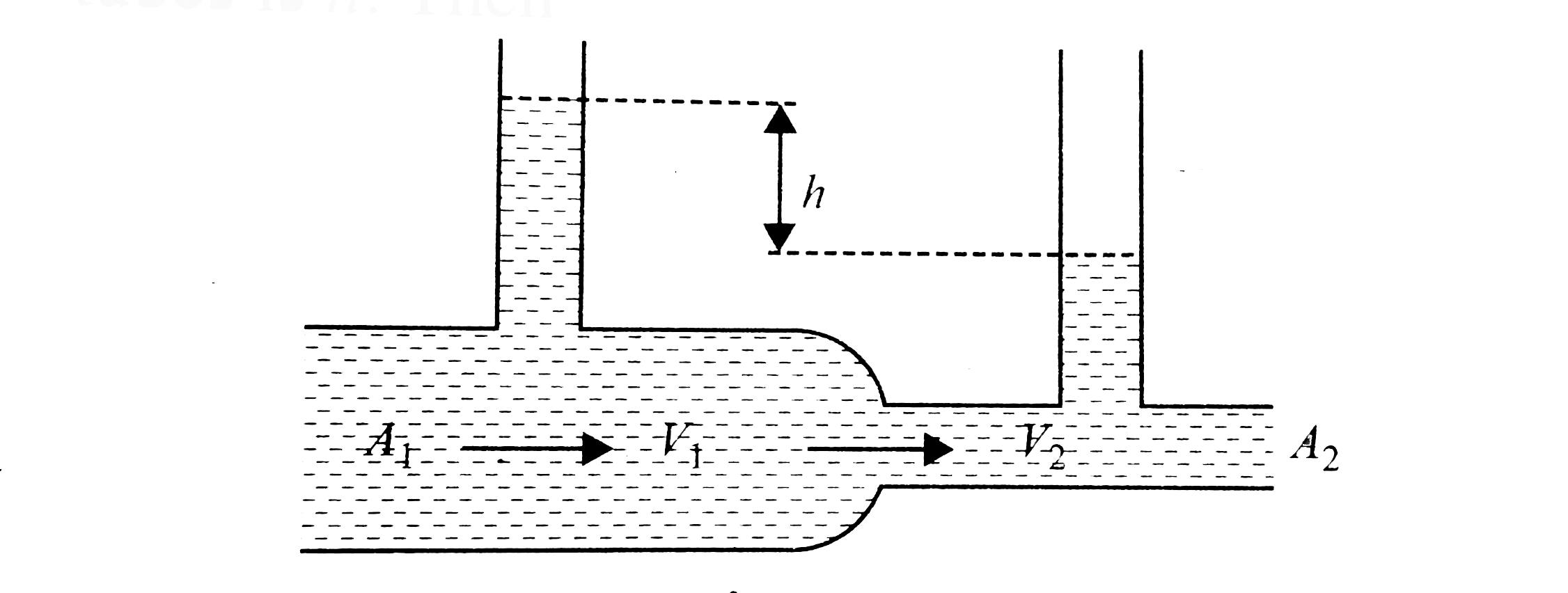
From a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.

The volume of the liquid flowing through the tube in time is A1v1
v2−v1=√2gh
v22−v11=2gh
The energy per unit mass of the liquid is the same in both sections of the tube
(c) p1ρ+v212=p2ρ+v222
or p1−p2=ρ2(v22−v21)
But p1−p2=ρgh=ρ2(v22−v21)
or v22−v21=2gh
Topper's Solved these Questions
- FLUID MECHANICSBOOK - BITSAT GUIDECHAPTER - FLUID MECHANICSEXERCISE - BITSAT Achives
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - BITSAT GUIDECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - All Questions
33 Videos
- GAUSS LAW AND ELECTRIC POTENTIAL THEORYBOOK - BITSAT GUIDECHAPTER - GAUSS LAW AND ELECTRIC POTENTIAL THEORYEXERCISE - BITSTAT ARCHIVES
4 Videos
Similar Questions
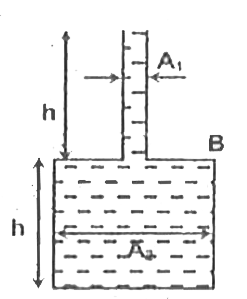
The vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
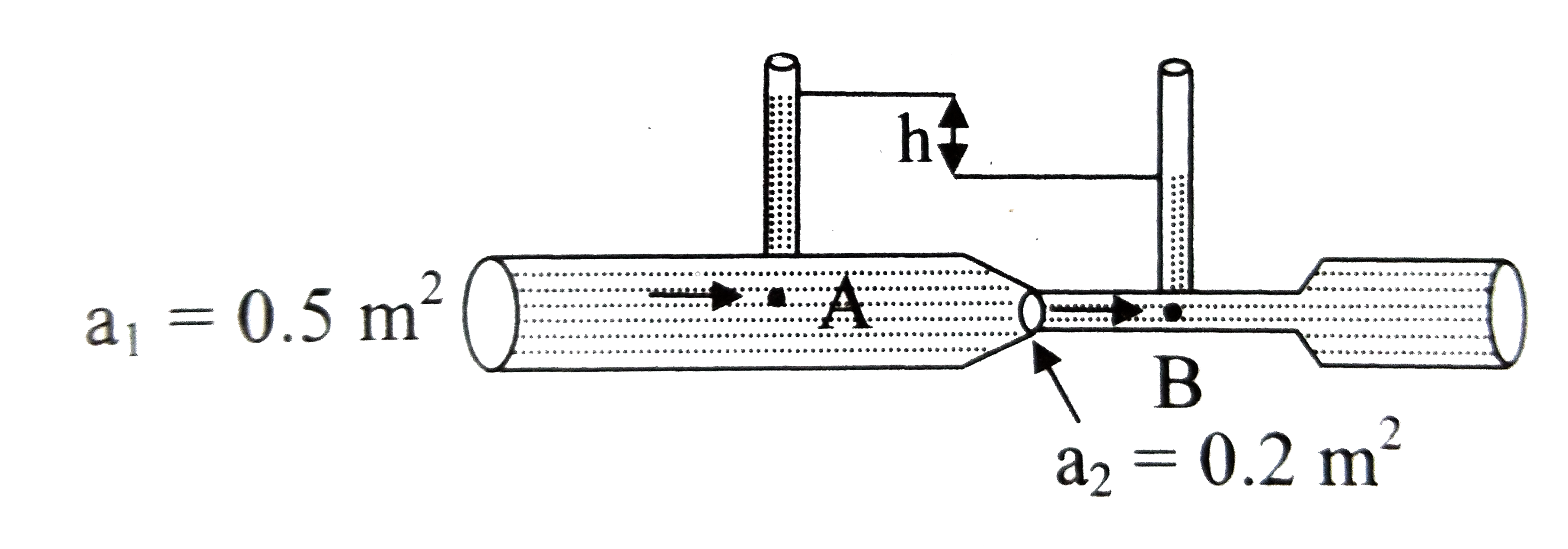
View SolutionAn incompressible, non-viscous liquis of density r flows through a horizontal tube as shown below. The flow condition is steady. Area of cross section at A and B are a1anda2 respectively. The height difference of liquid in two tubes inserted at A and B is h.
View Solution
Knowledge Check
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=ghA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
 Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube
Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tubeTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
AK1A2=K2A1BK1A1=K2A2CK1=K2DK1A1=K2A2
A liquid flows through a pipe of non-uniform cross-section. If A1andA2 are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
View SolutionA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is

View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionA liquid of density ρ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F. Choose the incorrect option.
View SolutionA container has a small hole at its bottom. Area of cross-section of the hole is A1 and that of the container is A2. Liquid is poured in the container at a constant rate Qm3s−1. The maximum level of liquid in the container will be
View Solution
