A liquid X of density 3.36g/cm3 poured in a U-tube which contains Hg. Another liquid Y is poured in left arm with heght 8 cm upper levels of X and Y are same. What is density of Y?
0.8g/c
1.2g/c
1.4g/c
1.6g/c
To solve the problem, we need to find the density of liquid Y in the U-tube setup where liquid X of known density is present. Let's go through the steps systematically.
Step 1: Understand the Setup
We have a U-tube with two arms. In one arm, we have liquid X with a density of 3.36 g/cm³, and in the other arm, we have liquid Y with a height of 8 cm. The upper levels of both liquids X and Y are the same.
Step 2: Determine the Height of Liquid X
Since the upper levels of liquid X and Y are the same, we can denote the height of liquid X as hX. Given that the height of liquid Y is 8 cm, we can express the height of liquid X as:
hX=hY+2cm=8cm+2cm=10cm
Step 3: Apply the Hydrostatic Pressure Principle
According to the hydrostatic pressure principle, the pressure exerted by the column of liquid X must equal the pressure exerted by the column of liquid Y plus the pressure exerted by the mercury (Hg) column.
The pressure exerted by a column of liquid is given by the formula:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
Step 4: Write the Pressure Balance Equation
For liquid X and liquid Y, the pressure balance can be written as:
ρXghX=ρYghY+ρHgghHg
Where:
- ρX=3.36g/cm3
- hX=10cm
- hY=8cm
- ρHg is the density of mercury (approximately 13.6 g/cm³)
Since g is common in all terms, we can cancel it out:
ρXhX=ρYhY+ρHghHg
Step 5: Substitute Known Values
Substituting the known values into the equation:
3.36g/cm3×10cm=ρY×8cm+13.6g/cm3×2cm
33.6=8ρY+27.2
Step 6: Solve for Density of Liquid Y
Now, rearranging the equation to solve for ρY:
33.6−27.2=8ρY
6.4=8ρY
ρY=6.48=0.8g/cm3
Final Answer
The density of liquid Y is 0.8g/cm3.
---
We have a U-tube with two arms. In one arm, we have liquid X with a density of 3.36 g/cm³, and in the other arm, we have liquid Y with a height of 8 cm. The upper levels of both liquids X and Y are the same.
Since the upper levels of liquid X and Y are the same, we can denote the height of liquid X as hX. Given that the height of liquid Y is 8 cm, we can express the height of liquid X as:
hX=hY+2cm=8cm+2cm=10cm
According to the hydrostatic pressure principle, the pressure exerted by the column of liquid X must equal the pressure exerted by the column of liquid Y plus the pressure exerted by the mercury (Hg) column.
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
For liquid X and liquid Y, the pressure balance can be written as:
ρXghX=ρYghY+ρHgghHg
Where:
- ρX=3.36g/cm3
- hX=10cm
- hY=8cm
- ρHg is the density of mercury (approximately 13.6 g/cm³)
ρXhX=ρYhY+ρHghHg
Substituting the known values into the equation:
3.36g/cm3×10cm=ρY×8cm+13.6g/cm3×2cm
33.6=8ρY+27.2
Now, rearranging the equation to solve for ρY:
33.6−27.2=8ρY
6.4=8ρY
ρY=6.48=0.8g/cm3
The density of liquid Y is 0.8g/cm3.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - BITSAT GUIDECHAPTER - FLUID MECHANICSEXERCISE - BITSAT Achives
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - BITSAT GUIDECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - All Questions
33 Videos
- GAUSS LAW AND ELECTRIC POTENTIAL THEORYBOOK - BITSAT GUIDECHAPTER - GAUSS LAW AND ELECTRIC POTENTIAL THEORYEXERCISE - BITSTAT ARCHIVES
4 Videos
Similar Questions
There are three different liquids ( liquid 1 , liquid 2 and liquid 3) having density 13.6 gm/cc ., 1.3 gm/cc and 0.8 gm/cc . Liquid 1 is poured separately into the two arms till upper surface of liquid 2 & 3 are same . What is the height of liquid 3 if height of liquid 2 is 16 cm ?
View SolutionLength of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View Solution
Knowledge Check
A monometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas 'A' as follows
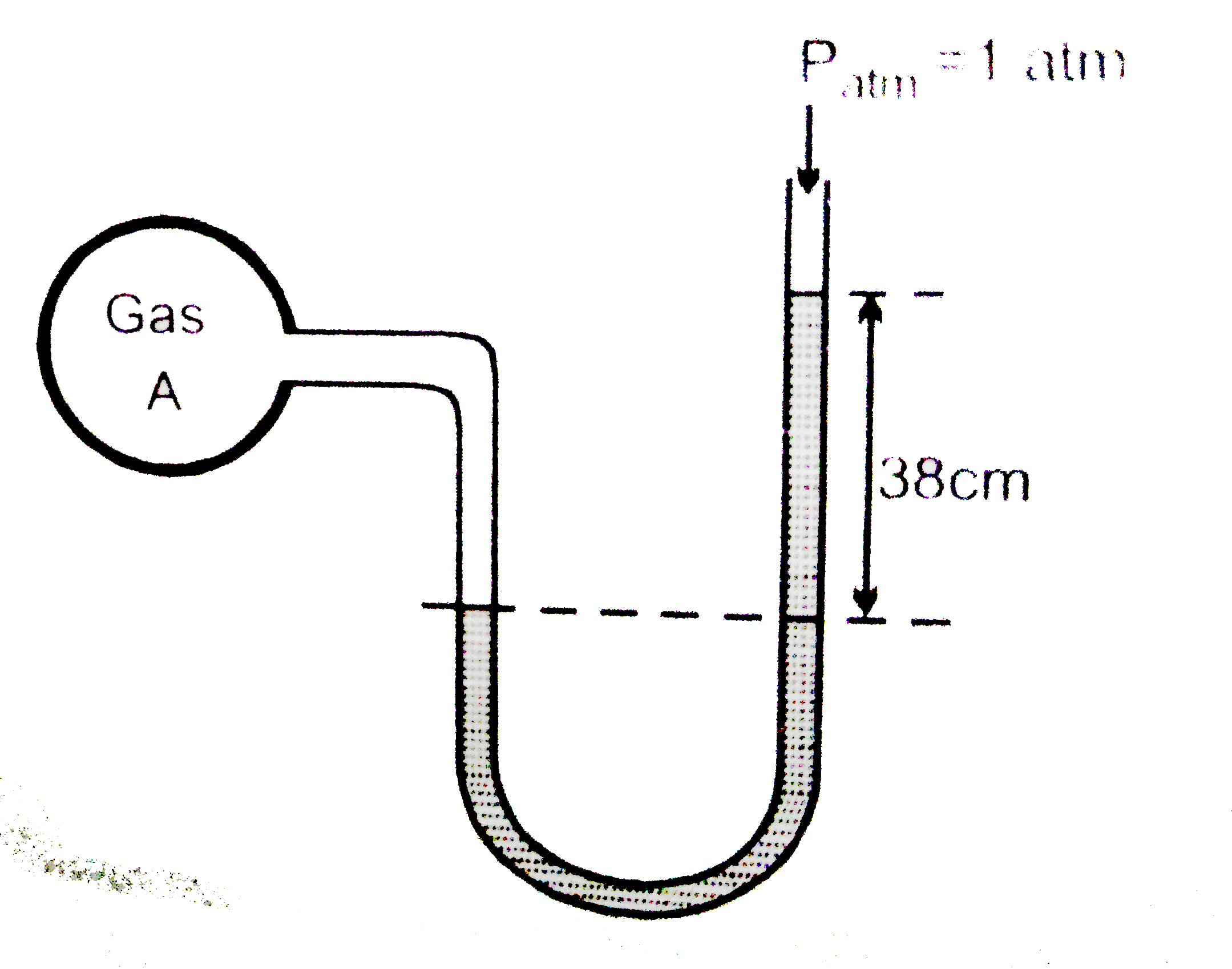
If the same liquid is used in barometer to measure the atmospheric pressure, then what will be the lengh of the liquid columnm which exerts pressure equal to 1 atm ? (density of Hg=13.6g/cm3)A190 cmB76 cmC30.4 cmD266 cm
A monometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas A'asfollows<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NRA_PHY_CHM_JMA_C03_E01_213_Q01.pngwh=80%sty≤=background:white;><br>Ifthesameliqusused∈¯ometer→measuretheatmosphericpressure,thenwˆwillbethe≤n>hoftheliquolumn,whichexertspressureequal→1atm?(densityofHg=13.6g//cm^(3))
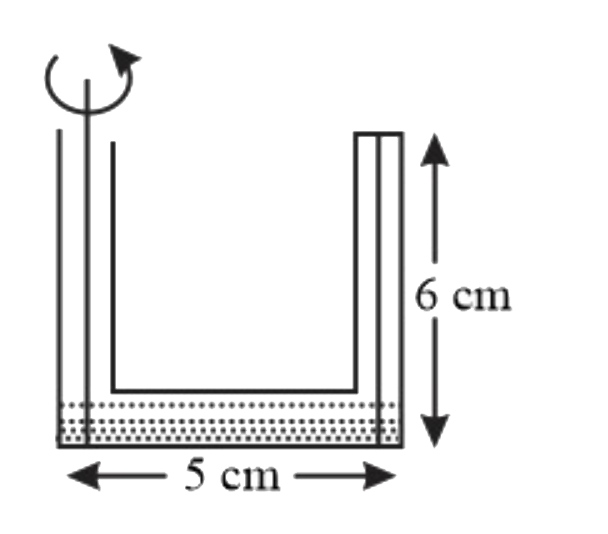
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View SolutionA U-tube having uniform cross-section but unequal arm length I1=100 cm and I2=50 cm has same liquid of density ρ1 filled in it upto a height h=30 cm as shown in figure. Another liquid of density ρ2=ρ1/2 is poured in arm. A Both liquids are immiscible What length of the second liquid (in cm) should be poured in A so that second overtone of A is in unison with fundamental tone of B. (Neglect end correction)
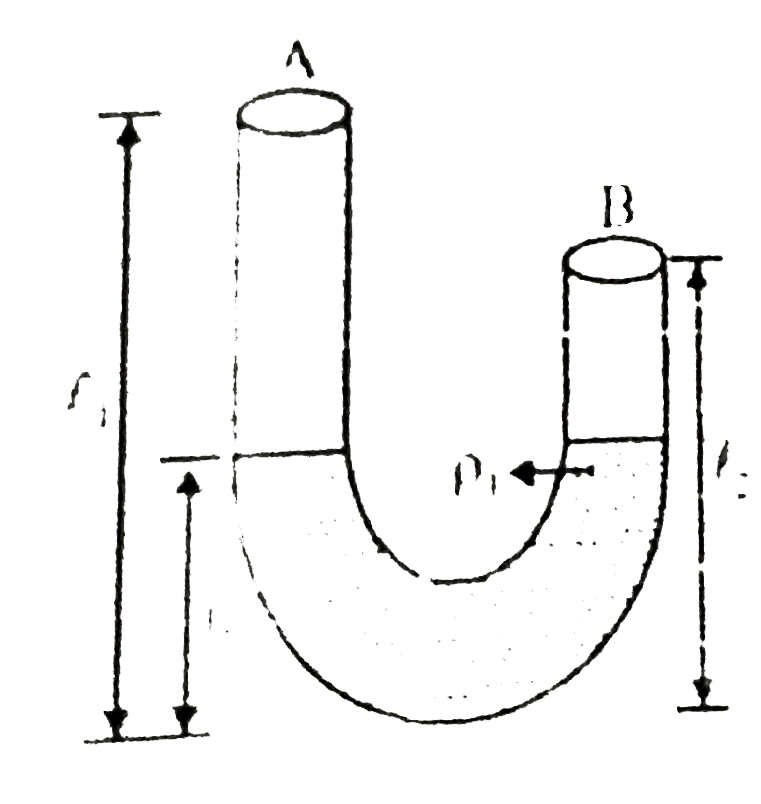
View SolutionA manometer tube contains a liquid of density 4×103kgm−3. When connected to a vessel containing a gas, the liquid level in the other arm of the tube is higher by 20 cm. When connected to another sample of enclosed gas, the liquid level in the other arm of the manometer tube falls 8 cm below the liquid level in the first arm. Which of the two samples exerts more pressure and by what amount ?
View SolutionA manometer tube contanins a liquid of density 3×103kgm−3. When connected to a vessel containing a gas, the liquid level in the other arm of the tube is higher by 10 cm. When connected to another sample of enclosed gas, the liquid level in the other arm of the manometer tube falls 7 cm below the liquid level in the first arm. Which of the two samples exerts more pressureand by what amount ?
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
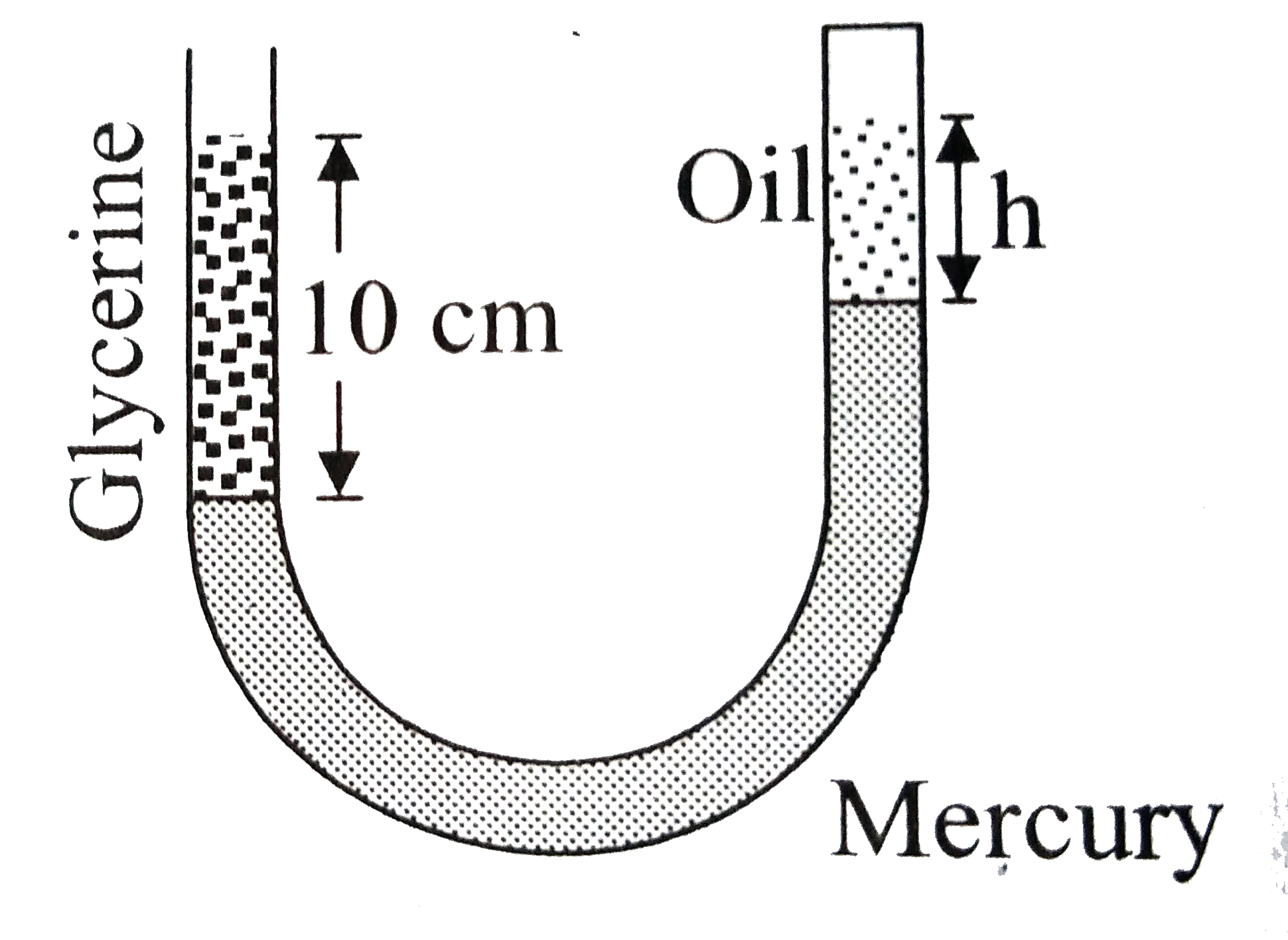
View SolutionA vertical U tube of uniform cross section contains mercury in both of its arms. A glycerine (d=1.3g/cm3) column of length 10cm is introduced into one of the arms. Oil of density 0.8g/cm3 is poured in the other arm until the upper surfaces of the oil and glycerine are in the same horizontal level. Find the length of oil column. Densit of mercury is 13.6g/cm3.

View Solution
