Length of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

The correct Answer is:5
Due to rotation let the shift of the liqu\id be xcm.
Let the cross sectoinal area of the tube of A.

In the right limb for compressed air,
p1v1=p2v2
p0A×6=p2a(6−x)
p2=6p16−x
Force at te corver C of right limb due to liquid above,
p1=[6p16−x+xρg]A
Mass of the liquid in the horizontal arm M=ρ(l−x)A
It is rotated about left limb. Then the cenripetal force is
F2=mω20r=ρ(l−x)Aω201+x2(l2−x2)
F2=mω20r=ρ(1=x)Aω201+x2=ρAω202(12−x2)
But F1=F2
⇒ρAω20(12−x2)2=[δρ0δ−x+xρx]A
=105×100x(212−x2)×10−42
=[δ×10500(δ−x)+x×105×10×10−2]
On solving we get x=0.01m=1cm
The length of the air column =6−1=5cm
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:True/False
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:SCQ_TYPE
Explore 13 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
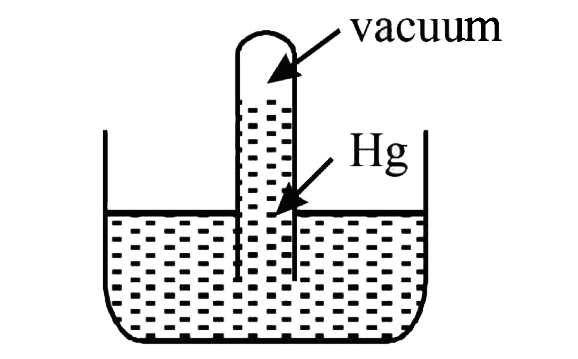
View SolutionA metal ball immersed in alcohol weights W1 at 0∘C and W2 at 50∘C. The coefficient of expansion of cubical the metal is less than that of the alcohol. Assuming that the density of the metal is large compared to that of alcohol, it can be shown that
View SolutionAssertion: Pascal law is the working principle of hydraulic lift.
Reason: Pressure =thrustarea
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionGravitational acceleration on the surface of the planet is √611g. where g is the gravitational acceleration on the surface of the earth. The average mass density of the planet is 23 times that of the earth. If the escape speed on the surface of the earth is taken to be 11kms−1 the escape speed on the surface of the planet in kms−1 will be
View SolutionA U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area =1cm^(2) , It is filled with water of volume 60 cc. What volume of a liquid of density 4g//cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?
View SolutionLength of a horizontal arm of ends of both the vertical arms pressure P0=105N/m2. A liquid of density ρ=103kg/m3 is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0=√40/3rad/sec. If length of each vertical arm is a=1m and in the sealed end liquid rises to a height y=1/2m, find pressure in the sealed tube during rotation. (in ×105N/m2)

View SolutionA tube of length 'L' is filled completely with an in compressiblem liquid of mass 'M' and closed at both ends. The tube is then rotated in a horizontal plane about one of it's ends with a uniform angular velocity 'ω'. Then which of following statements are true :
View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionLength of a horizontal arm of U-tube is L and ends of both the vertical arms are open to atompsheric pressure P_(0) , A liquid of density rho is poured in the tube such that liquid just fills the horizontal part of the tube as shown in figure . Now one end of the opened ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed omega_(0) . if length of each vertical arm is a and in the sealed end liquid rises to a height y, find pressure in the sealed tube during rotation.
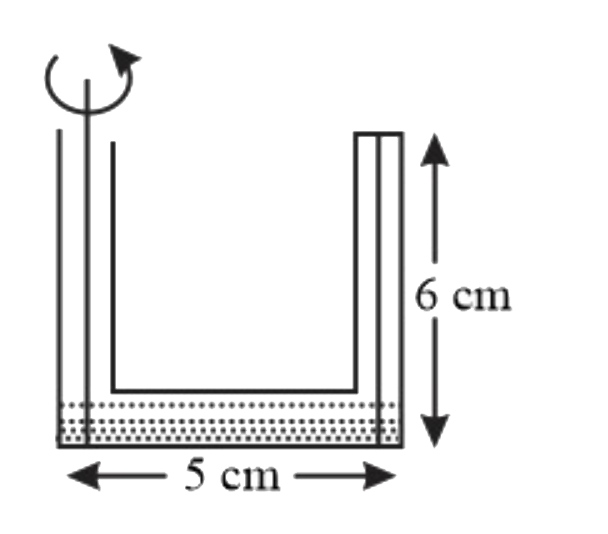
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
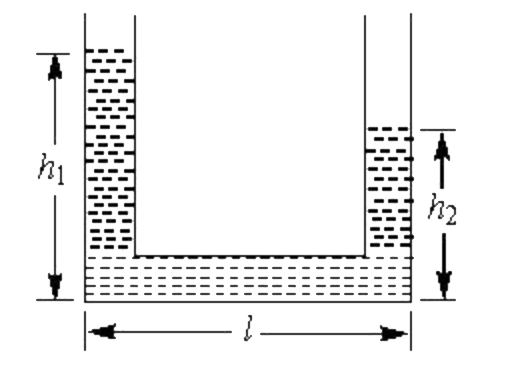
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
View SolutionThe arms of a vertical U tube of uniform inner cross section contains mercury. In one of the arms of the tube, water column of length 8 cm is introduced. In the other arm, oil of density 0.75 g/cm ""^(3) is poured till the upper surfaces of water and oil are at same horizontal level. Calculate the length of oilcolumn.
View SolutionA liquid can rise to a height of h in a capillary tube of length l (l>h). The tube filled with the liquid is kept horizontal with its two ends open. Now the tube is kept vertical with the liquid in it. Some liquid flows out. Find the height of the liquid remaining in the tube if the surface tension of the liquid is σ.
View SolutionLength of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View Solution

