A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area=1cm2, It is filled with water of volume 60 cc. What volume of a liquid of density 4g/ should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?
60cc
45cc
50cc
35cc
The correct Answer is:D
To solve the problem step by step, we need to determine how much liquid of density 4g/cc should be poured into one side of the U-tube so that no water remains in the horizontal arm.
Step 1: Understand the setup
We have a U-tube with:
- Length of the horizontal arm = 20 cm
- Cross-sectional area = 1cm2
- Volume of water = 60 cc
Step 2: Calculate the height of water in the U-tube
The volume of water is given as 60 cc. Since the cross-sectional area is 1cm2, we can calculate the height of the water column in the U-tube using the formula:
Volume=Area×Height
Thus,
60cc=1cm2×Height
This gives us:
Height=60cm
Step 3: Determine the pressure balance
When we pour the liquid of density 4g/cc into one side of the U-tube, we want the pressure at the bottom of both sides to be equal.
Let:
- h = height of the liquid of density 4g/cc poured into one side.
- The pressure exerted by the water column on the left side will be P1=ρ1gh1 (where ρ1=1g/cc for water and h1=60cm).
- The pressure exerted by the liquid on the right side will be P2=ρ2gh2 (where ρ2=4g/cc and h2=h).
Step 4: Set up the equation for pressure balance
Since the pressures at the same level must be equal:
P1=P2
This gives us:
ρ1gh1=ρ2gh2
Substituting the values:
1g/cc×60cm=4g/cc×h
Cancelling g from both sides:
60=4h
Thus,
h=604=15cm
Step 5: Calculate the total volume of the liquid
Now, we need to find the total volume of the liquid in the U-tube:
1. The volume of the liquid of density 4g/cc in the left limb:
Vleft=Area×Height=1cm2×15cm=15cm3
2. The volume of the liquid in the horizontal arm:
Vhorizontal=Area×Length=1cm2×20cm=20cm3
Step 6: Total volume of liquid
Adding both volumes:
Vtotal=Vleft+Vhorizontal=15cm3+20cm3=35cm3
Conclusion
The volume of the liquid of density 4g/cc that should be poured into the U-tube is 35cm3.
---
We have a U-tube with:
- Length of the horizontal arm = 20 cm
- Cross-sectional area = 1cm2
- Volume of water = 60 cc
The volume of water is given as 60 cc. Since the cross-sectional area is 1cm2, we can calculate the height of the water column in the U-tube using the formula:
Volume=Area×Height
Thus,
60cc=1cm2×Height
This gives us:
Height=60cm
When we pour the liquid of density 4g/cc into one side of the U-tube, we want the pressure at the bottom of both sides to be equal.
- h = height of the liquid of density 4g/cc poured into one side.
- The pressure exerted by the water column on the left side will be P1=ρ1gh1 (where ρ1=1g/cc for water and h1=60cm).
- The pressure exerted by the liquid on the right side will be P2=ρ2gh2 (where ρ2=4g/cc and h2=h).
Since the pressures at the same level must be equal:
P1=P2
This gives us:
ρ1gh1=ρ2gh2
Substituting the values:
1g/cc×60cm=4g/cc×h
Cancelling g from both sides:
60=4h
Thus,
h=604=15cm
Now, we need to find the total volume of the liquid in the U-tube:
1. The volume of the liquid of density 4g/cc in the left limb:
Vleft=Area×Height=1cm2×15cm=15cm3
2. The volume of the liquid in the horizontal arm:
Vhorizontal=Area×Length=1cm2×20cm=20cm3
Adding both volumes:
Vtotal=Vleft+Vhorizontal=15cm3+20cm3=35cm3
The volume of the liquid of density 4g/cc that should be poured into the U-tube is 35cm3.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Length of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
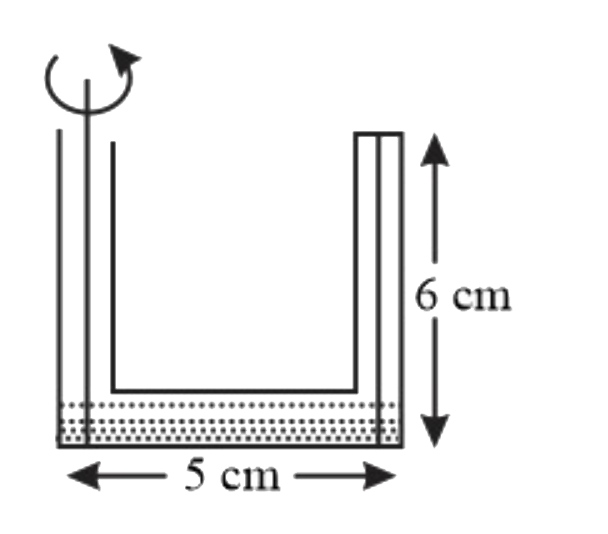
View Solution
Knowledge Check
A U - tube having a horizontal arm of length 20 cm, has a uniform cross - sectional area 1cm2. It is filled with water of volume 60 cc. The volume of a liquid of density 4 g cc−1 required to be poured in one arm of the U - tube so that no water is left in the horizontal arm of the tube is (take g =9.8ms−2)
A60 ccB45 ccC50 ccD35 ccA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is
 AF=0BρAv2C2ρAv2D12ρAv2
AF=0BρAv2C2ρAv2D12ρAv2A U tube pf uniform born of cross sectional area A has been set up vertically with open ends facing up Now mgm of a liquid of density d is poured into it. The column of liquid in this tube will oscillation with a period T such that
AT=2π√MgBT=2π√MAgdCT=2π√MgdADT=2π√M2Adg
There is a U-tube of different cross sectional area A=2.5cm2 and 4A of limbs fitted with the frictionless pistons each of mass m= 1 kg. An ideal liquid of density ρ=2000kg/m3 is filled in the tube and the tube is accelerated in horizontal direction with a constant acceleration 'a'. Find the value of acceleration 'a' (in m/s2 ) for which both pistons stay in the same horizontal level. The length of horizontal section of U-tube is l =1 m. (Take g=10m/s2 )
View SolutionThe plastic tube in Fig. has a cross-sectional area of 5.00 cm2. The tube is filled with water until the short arm (of length d = 0.800 m) is full. Then the short arm is figure sealed and more water is gradually poured into the long arm. When the total height of water in the long arm reaches 2.80 m, the seal is on the verging of popping. What force is then on the seal?
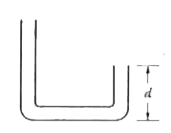
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionA cylindrical tube of cross sectional area 20cm2 is filled with water to a height of 10cm. The tube carries a tight fitting piston of negligible mass. What will be the pressure exerted at the bottom of the tube when a mass of 2 kg placed on the piston? Atmospheric pressure can be ignored.
View Solution_E01_110_Q01.png)
The U-tube shown has uniform cross-section A liquid is filled in the two arms up to height h1 and h2 and then the liquid is allowed to move neglect viscosity and surface tension. When the levels equalize in the two arms, the liquid will
View Solution