A circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

Let us find the pressure at the lowes point 1. Sicne the liquid has density ρ2 and height of liquid column is h′2 on the right and side of point 1 we have
P1=ρ1gh1……i

Since two liquid coluns of heights h1 and h2 and densities ρ1 and ρ2 are situated above point 1, on the left hand side, we have
P2=ρ1gh2+ρ2gh′2.............ii
Equating P1 and P2 from eqn i and ii we have
ρ1h2+ρ2h′2=ρ1h1...........iii
Substituting h′2=Rsinθ+Rcosθ,h2=R(1−cosθ) and h1=R(1−sinθ) in eqn iii we have
ρ1R(1−cosθ)+ρ2R(sinθ+cosθ)=ρ1R(1−sinθ)
This gives
cosθ+sinθcosθ−sinθ=ρ1ρ2⇒tanθ=ρ1−ρ2ρ1+ρ2
Then θ=tan−1(ρ1−ρ2ρ1−ρ3)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

View SolutionTwo non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________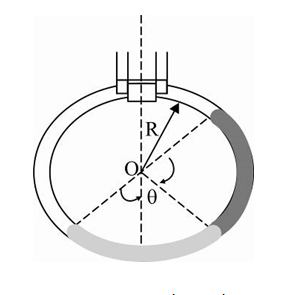
View Solution
Knowledge Check
If two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
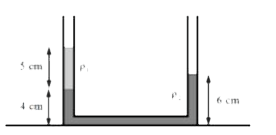
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2The figure represents a U-tube of uniform cross-section filled with two immiscible liquids. One is water with density ρw and the other liquid is of density ρ . The liquid interface lies 2cm above the base. The relation between ρ and ρw is
 .Aρ=ρwBρ=1.02ρwCρ=1.2ρwDNone of these
.Aρ=ρwBρ=1.02ρwCρ=1.2ρwDNone of theseA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
 A13B25C12D45
A13B25C12D45
Two non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
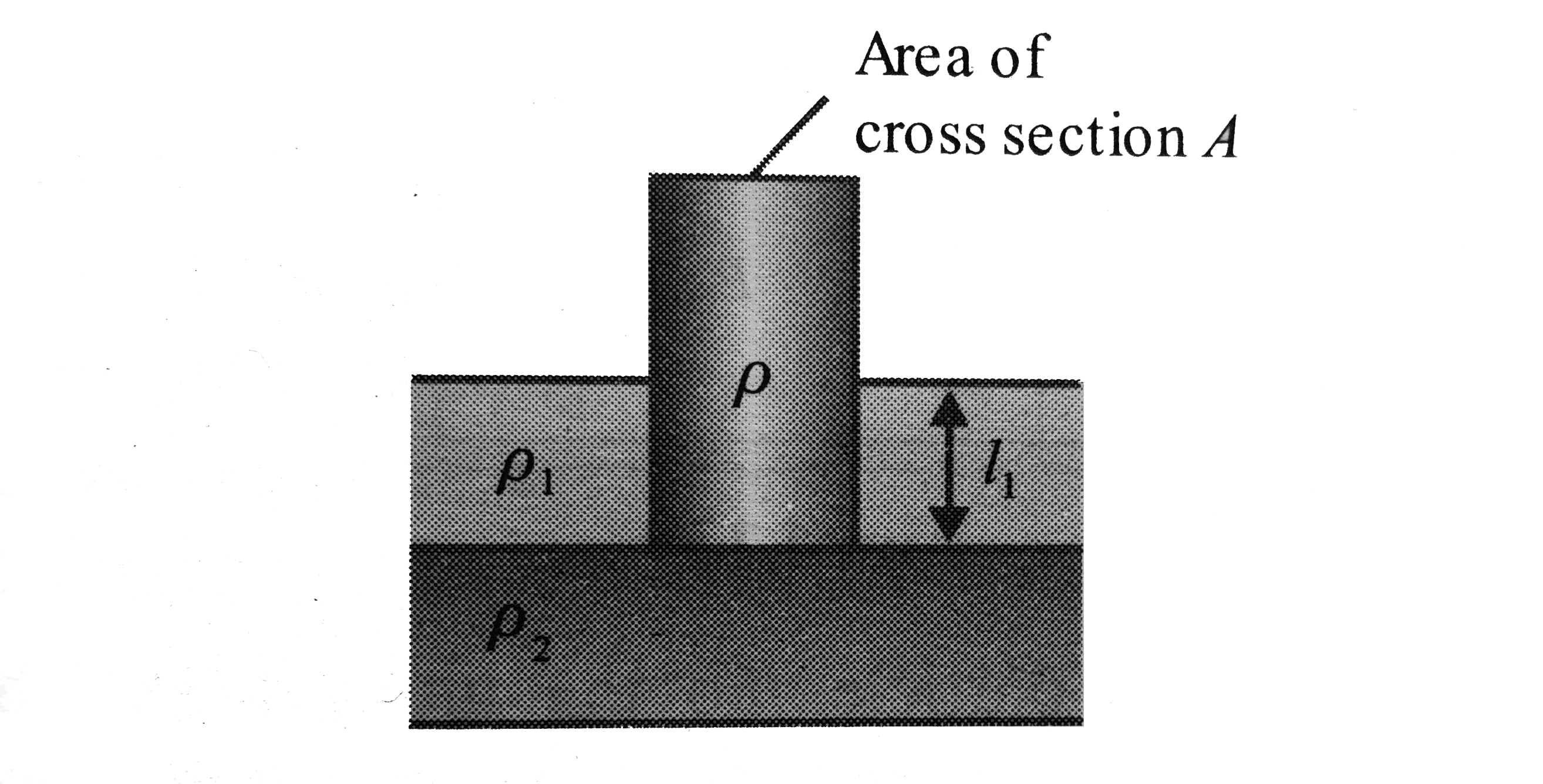
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View SolutionTwo liquids of densities ρ and 3rho having volumes 3V and V are mixed together. Find density of the mixture.
View SolutionA test tube of uniform cross-section is floated vertically in a liquid 'A' (density ρA) upto a mark on it when it is filled with 'x' ml of a liquid 'B' (density ρB). To make the test tube float in liquid B upto the same mark it is filled with y ml of the liquid A. Find the mass of the test tube.
View SolutionIf two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
View Solution
