A conducting ball is given a certain charge and fixed at point P. An another point charge of mass 1 gm and charge 20μC when kept at Q (3m, 9m) starts moving with acceleration →a=(1.08ˆi+1.44ˆj)ms−2. The potential at Q is +720 volt. Calculate
(a) charge given to ball
(b) position of the ball.
To solve the problem step by step, we need to calculate the charge given to the conducting ball and the position of the ball based on the provided information.
Given Data:
- Mass of the point charge m=1g=1×10−3kg
- Charge of the point charge Q2=20μC=20×10−6C
- Position of point Q is (3m,9m)
- Acceleration →a=(1.08^i+1.44^j)m/s2
- Electric potential at Q is V=720V
Step 1: Calculate the Charge on the Conducting Ball
The electric potential V at a distance r from a point charge Q1 is given by:
V=kQ1r
where k=14πϵ0≈9×109N m2/C2.
From the problem, we know:
720=9×109⋅Q1r
Thus,
Q1=720⋅r9×109
Step 2: Determine the Distance r
The distance r between the conducting ball (at point P) and the point charge at Q can be calculated using the coordinates. Let the coordinates of point P be (x,y). Then:
r=√(3−x)2+(9−y)2
Step 3: Calculate the Force Acting on the Point Charge
The force F acting on the point charge is given by:
F=m⋅a
Substituting the values:
F=(1×10−3)⋅(1.08^i+1.44^j)=(1.08×10−3^i+1.44×10−3^j)N
Step 4: Relate Force to Charge
The force due to the electric field from the conducting ball is given by:
F=kQ1Q2r2
Setting the two expressions for force equal gives:
kQ1Q2r2=m⋅a
Step 5: Substitute Values
Substituting Q2=20×10−6C and rearranging gives:
Q1=m⋅a⋅r2kQ2
Substituting the known values:
Q1=(1×10−3)⋅(1.8)⋅r29×109⋅(20×10−6)
Step 6: Solve for Q1
To find r, we can use the potential equation:
r=720⋅Q19×109
Substituting this back into the equation for Q1 will allow us to solve for Q1.
Step 7: Find Position of the Ball
Using the derived equations, we can find the coordinates (x,y) of point P by solving the equations derived from the force and potential relationships.
Final Calculation
After substituting and simplifying, we find:
1. The charge Q1 on the conducting ball.
2. The coordinates of point P.
- Mass of the point charge m=1g=1×10−3kg
- Charge of the point charge Q2=20μC=20×10−6C
- Position of point Q is (3m,9m)
- Acceleration →a=(1.08^i+1.44^j)m/s2
- Electric potential at Q is V=720V
The electric potential V at a distance r from a point charge Q1 is given by:
V=kQ1r
where k=14πϵ0≈9×109N m2/C2.
720=9×109⋅Q1r
Thus,
Q1=720⋅r9×109
The distance r between the conducting ball (at point P) and the point charge at Q can be calculated using the coordinates. Let the coordinates of point P be (x,y). Then:
r=√(3−x)2+(9−y)2
The force F acting on the point charge is given by:
F=m⋅a
Substituting the values:
F=(1×10−3)⋅(1.08^i+1.44^j)=(1.08×10−3^i+1.44×10−3^j)N
The force due to the electric field from the conducting ball is given by:
F=kQ1Q2r2
Setting the two expressions for force equal gives:
kQ1Q2r2=m⋅a
Substituting Q2=20×10−6C and rearranging gives:
Q1=m⋅a⋅r2kQ2
Substituting the known values:
Q1=(1×10−3)⋅(1.8)⋅r29×109⋅(20×10−6)
To find r, we can use the potential equation:
r=720⋅Q19×109
Substituting this back into the equation for Q1 will allow us to solve for Q1.
Using the derived equations, we can find the coordinates (x,y) of point P by solving the equations derived from the force and potential relationships.
After substituting and simplifying, we find:
1. The charge Q1 on the conducting ball.
2. The coordinates of point P.
Topper's Solved these Questions
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - I
Explore 24 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - II
Explore 13 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS
Explore 4 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBook:FIITJEEChapter:ELECTROMAGNETIC WAVE & WAVE OPTICSExercise:ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
Explore 21 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
Similar Questions
A positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA positive charge 'Q' is fixed at a point A negatively charged particle of mass ' 'm' and charge 'q' is revolving in a circular path of radius r1 ,with Q' as the centre.The change in potential energy to change the radius of the circular path from r1 to r2 in joule is
View Solution
Knowledge Check
A ball of mass m1 moving with a certain speed collides elastically with another ball of mass m2 kept at rest . If the first ball starts moving in reversed direction after the impact then
Am1=m2Bm1>m2Cm1<m2DNone of theseA point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi storey building of height h. Find the position of the point charge q when it is in equilibrium
 A√(qQ4πε0mg)BQh2CqhmDnone of these
A√(qQ4πε0mg)BQh2CqhmDnone of theseAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
A236.8N/CB200N/CC23N/CD250N/C
A charged particle of mass m and charge q is kept initially at rest on a frictionless surface. Another charged particle of mass 4m and charge 2q starts moving with velocity v towards it. Calculate the distance of the closest approach for both the charged particles.
View SolutionElectric field intensity at a point B due to a point charge Q kept at a point charge Q kept at point A is 24NC−1, and electric potential at B due to the same charge is 12JC−1. Calculate the distance AB and magnitude of charge.
View SolutionA positive charge Q is fixed at a point in space. There is another charge -q, which moves in a circular path of radius r around the given fixed charge . Assume that the electrostatic force between them is the only force acting on them. Calculate time period of revolution of charge .
View SolutionThe potential of a charge q1 is +10V at the point P .When we bring another charge q2 ,the potential at P becomes 4V.Then q2 is
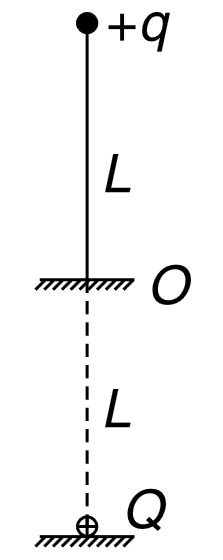
View SolutionA particle of mass m and charge q is attached to a light insulating thread of length L. The other end of the thread is secured at point O. Exactly below point O, there is a small ball having charge Q fixed on an insulating horizontal surface. The particle remains in equilibrium vertically above the ball with the string taut. Distance of the ball from point O is L. Find the minimum value of Q for which the particle will be in a stable equilibrium for any gentle horizontal push given to it.
View Solution

