A uniform electric field of intensity E=106V/m exist in vertically downwards direction in a region. A particle of mass m = 0.01 kg andcharge q=10−6C is suspended byan inextensible thread oflength I=1m. The particle is displaced slightly from its mean position and released. Calculate the time period ofits oscillation. What minimum velocity should be given to the particle at rest from its equilibrium position so that it completes a full circle in vertical plane? Calculate the maximum and minimum tension in the thread in its circular motion in vertical plane. [0.6s,23.42m/s,6.59N,0]
(a) 0.6sec (b) 23.42m/s (c ) 6.588N, Zero
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - I
24 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - II
13 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS
4 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
A particle is executing SHM of amplitude 10 cm. Its time period of oscillation is π seconds. The velocity of the particle when it is 2 cm from extreme position is
View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View Solution
Knowledge Check
A particle performing S.H.M., its velocity when the particle moves from mean to extreme position is
Aslower initially and faster laterallyBuniformly movesCfaster initially and momentraily falls to zeroDfast moves and stop at extreme positionA particle is executing S.H.M.if v1 and v2 are the velocities of the particle at distances x1 and x2 from mean position respectively , then time period of oscillation is
A2π ⎷(x22+x21)(V21+V22)B2π ⎷(x22−x21)(V21−V22)C2π ⎷(x22−x21)(V22−V21)D2π ⎷(x21−x22)(V21+V22)A particle of mass m is suspended from a fixed O by a string of length L. At t=0, it is displaced from its equilibrium position and released. The graph which shows the variation of the tension T in the string with time t is :
 A
A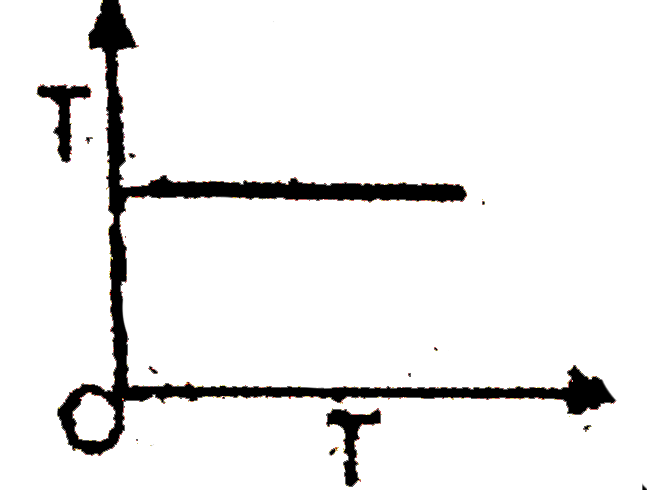 B
B C
C D
D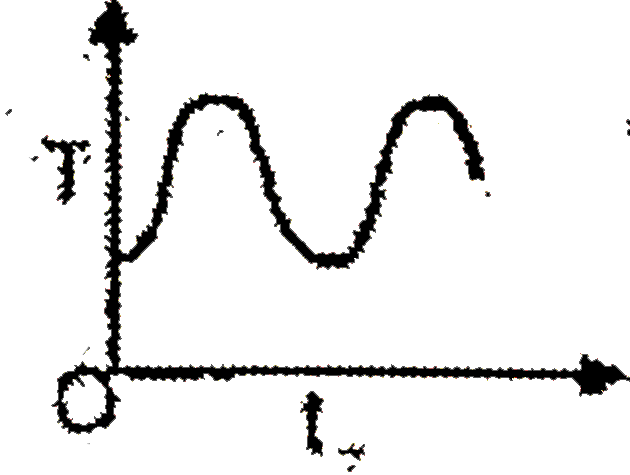
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA particle oscillates, according to the equation x = 5 cos (πt/2) m. Then the particle moves from equilibrium position to the position of maximum displacement in time of
View SolutionA particle of mass m is released from rest and follows a particle as a function of time?
View SolutionA water particle of mass 10.0 mg and having a charge of 1.50×10−6C stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View Solution
