A magnetic field B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d, Fig. The wires are in the x-y plane. The wire AB (of length d) has resistance R and parallel wires have negligible resistance. If AB is moving with velocity υ, what is the current in the circuit ? What is the force needed to keep the wire moving at constant velocity ?
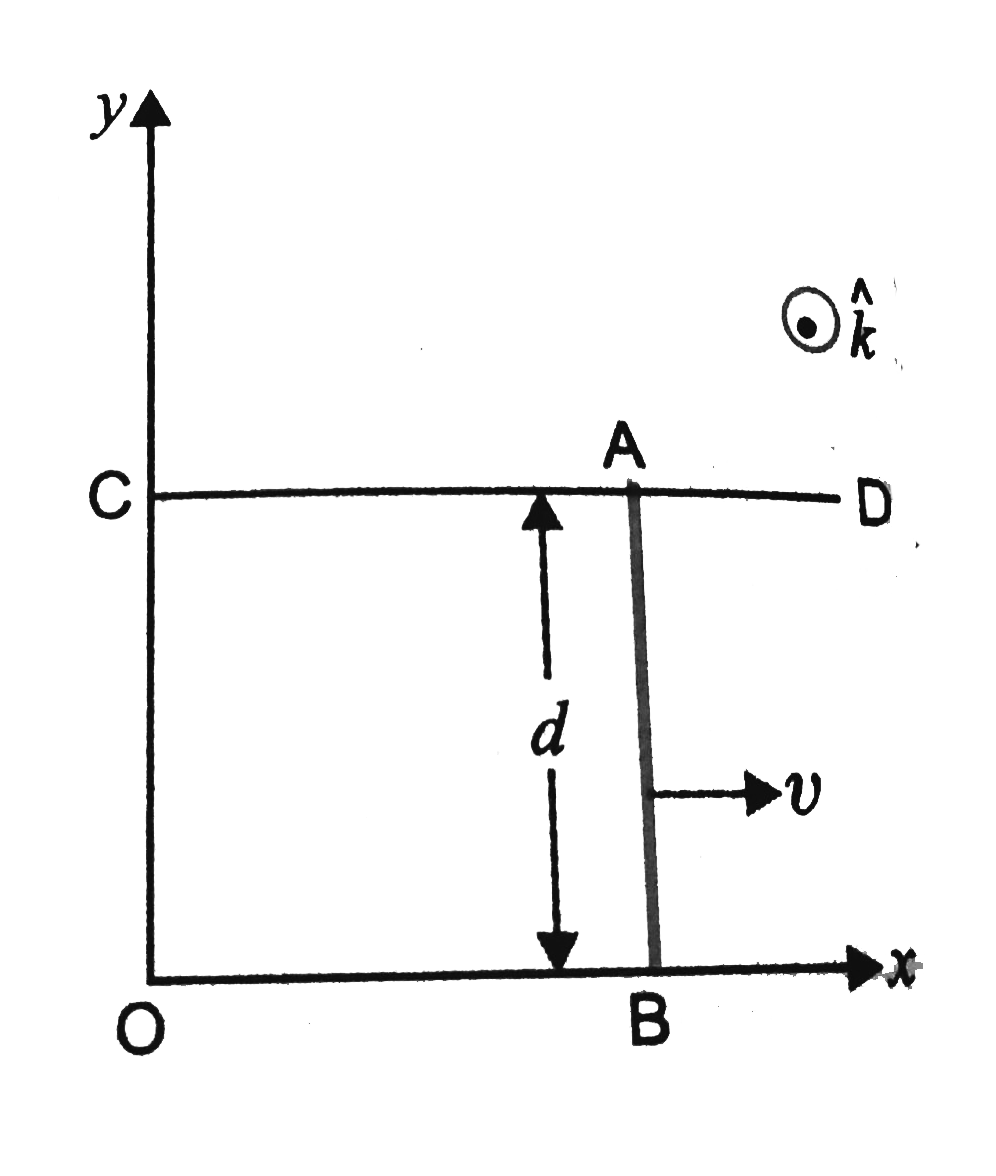
Let us assume that the parallel wires at are y=0 i.e., along x-axis and y=d. At t=0, AB has x=0, i.e, along y-axis and moves with a velocity v. Let at time t, wire is at x(t)=vt.
Now, the motional emf across AB is =(B0sinωt)vd(−ˆj)
emf due to change in field (along) OBAC)
=−B0ωcosωtx(t)d
Total emf in the circuit =emf due to change in field (along OBAC)+the motional emf across AB
=−B0d[ωxcos(ωt)+vsin(ωt)]
Electric current in clockwise direction is given by
=B0dR(ωxcosωt+vsinωt)
The force acting on the conductor is given by F=ilBsin90∘=ilB
Substituting the values, we have
Force needed along i=B0dR(ωxcosωt+vsinωt)×dxxB0sinωt
=B20d2R(ωxcosωt+vsinωt)sinωt
This is the required expression for force.
Topper's Solved these Questions
Similar Questions
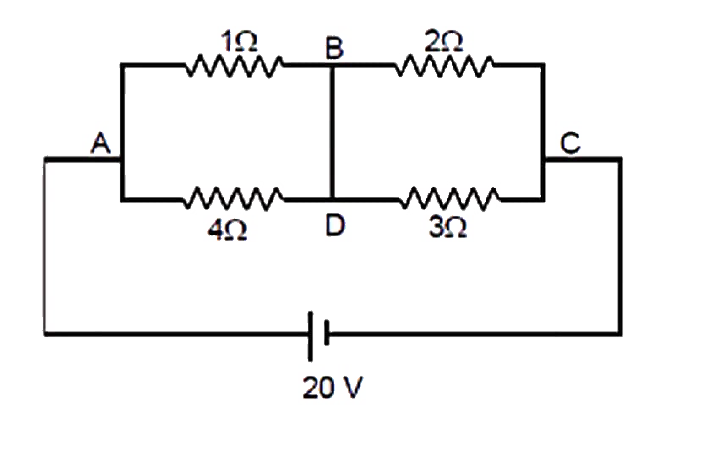
In the given circuit diagram , a connecting wire of negligible resistance is joining the points B and D, the current in the connecting wire is
View SolutionA wire having a resistance of 18Ω is cut into three equal parts. What is the equivalent resistance if these three parts are joined in parallel ?
View Solution
Knowledge Check
Figure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
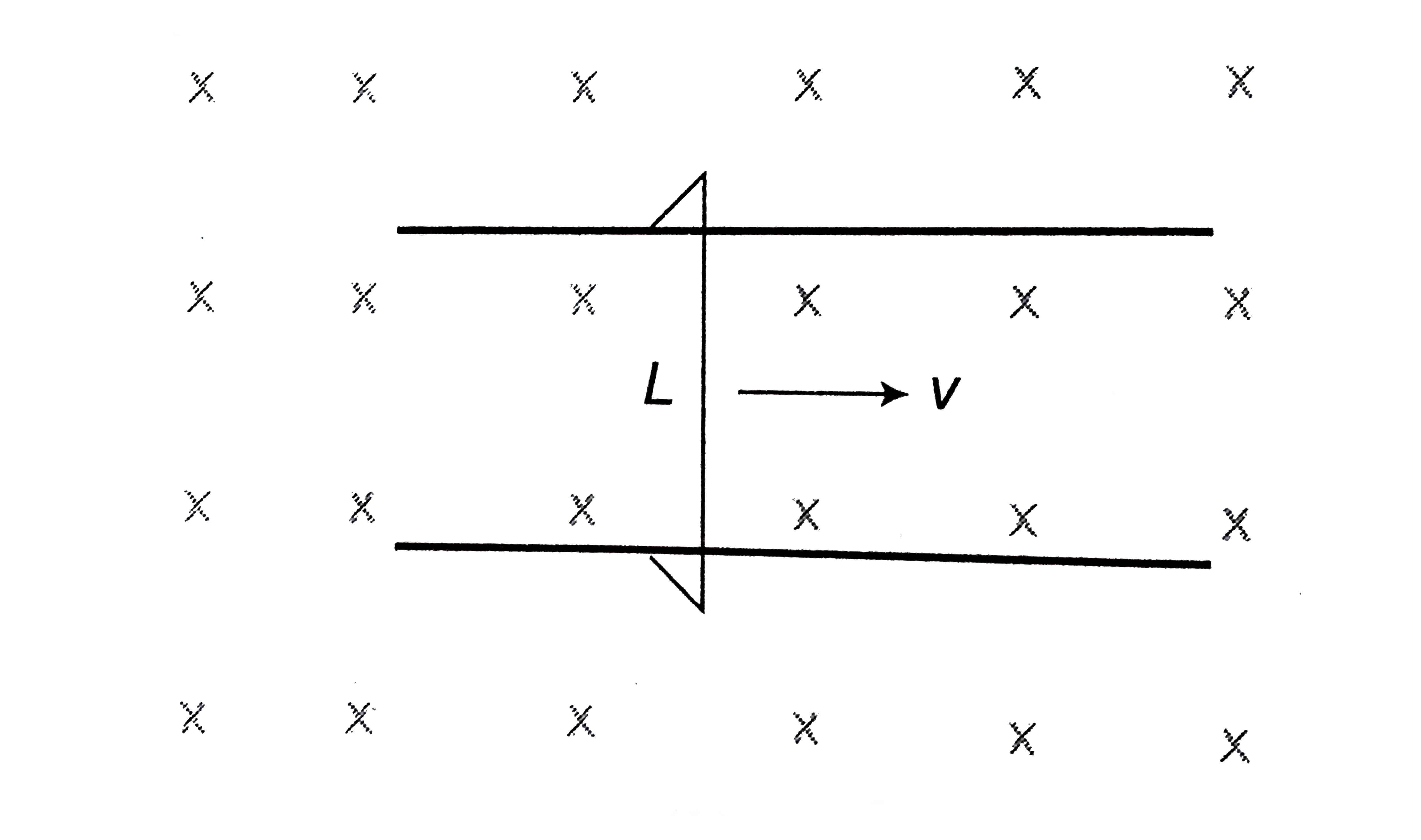 ABvLBBv2LCzeroDB2v2L/R
ABvLBBv2LCzeroDB2v2L/RThe resistance of a wire of length l and diameter d is R. The wire is stretched to double its length. The resistance of the wire will now be
AR2B2RC4RD16RWe have two wires A and B of same mass and same material. The diameter of wire A is half of that of B. If the resistance of the wire A is 24 Ω , then the resistance of the wire B will be
A12ΩB3ΩC1.5ΩD48Ω
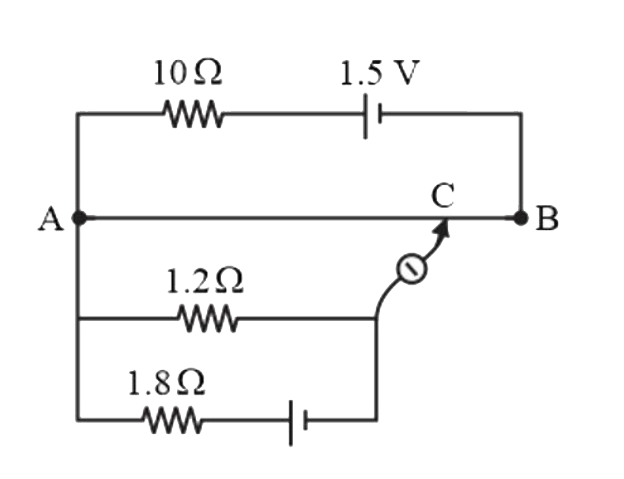
In the below circuit , AB is a wire of length 100 cm with 5Ω resistance . If there is no deflection in the galvanometer , the current flowing in the wire AB is
View SolutionTwo metallic wires A and B are connected in parallel. Wire A has length l and radius r, wire B has a length 2 l and radius 2r. Compute the ratio of the total resistance of parallel combination and the resistance of wire A.
View SolutionA wire has a resistance of 16Ω. It is melted and drawn into a wire of half its length. Calculate the resistance of the new wire. What is the percentage change in its resistance ?
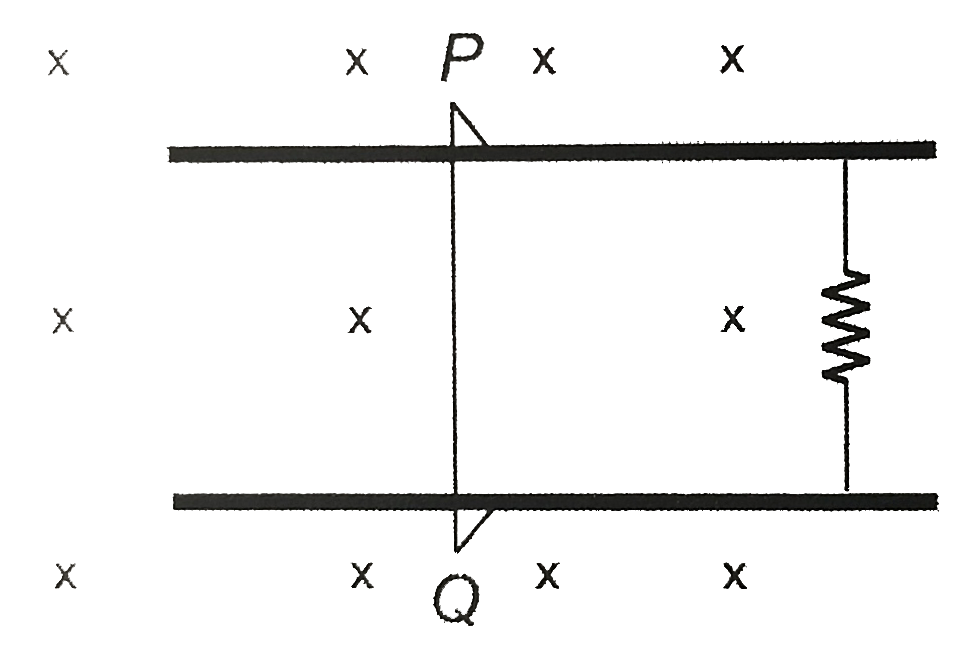
View SolutionConsider the situation shown in the figure. The wire PQ has mass m , resistance r and can slide 0n the smooth, horizontal parallel rails separated by a distance l . The resistance of the rais is negiligible. A uniform magnetic field B exists in the reactangular region and a resistance R connects the rail outside the field region. At t=0 , the wire PQ is pushed toward right with a speed v0 . Find
(a) the current in the loop at an instant when the speed of the wire PQ is v
(b) the acceleration of the wire as this instant
(c) the velocity v as a function of x
(d) the maximum distance the wire will move
(e) the velocity as a function of time
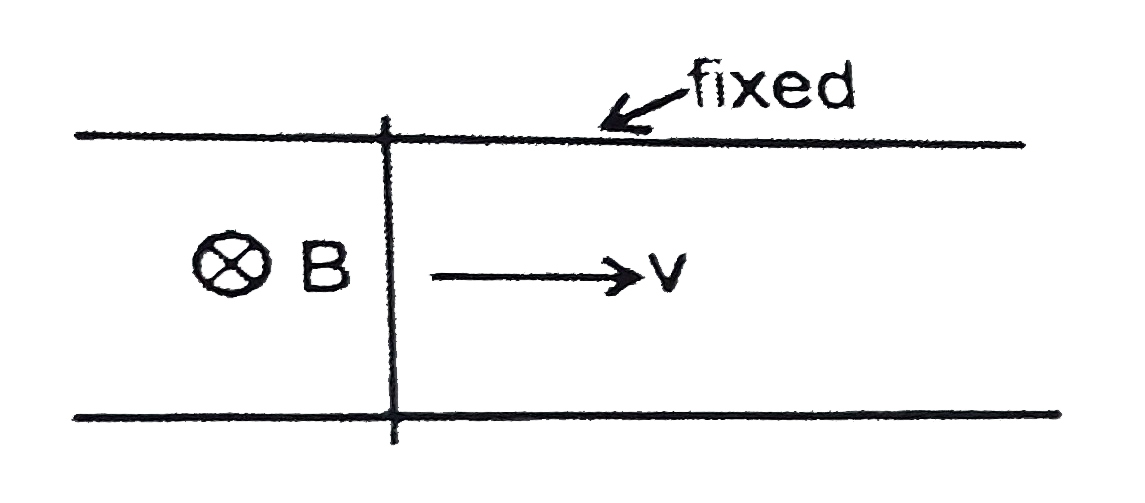
View SolutionFigure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
View Solution
