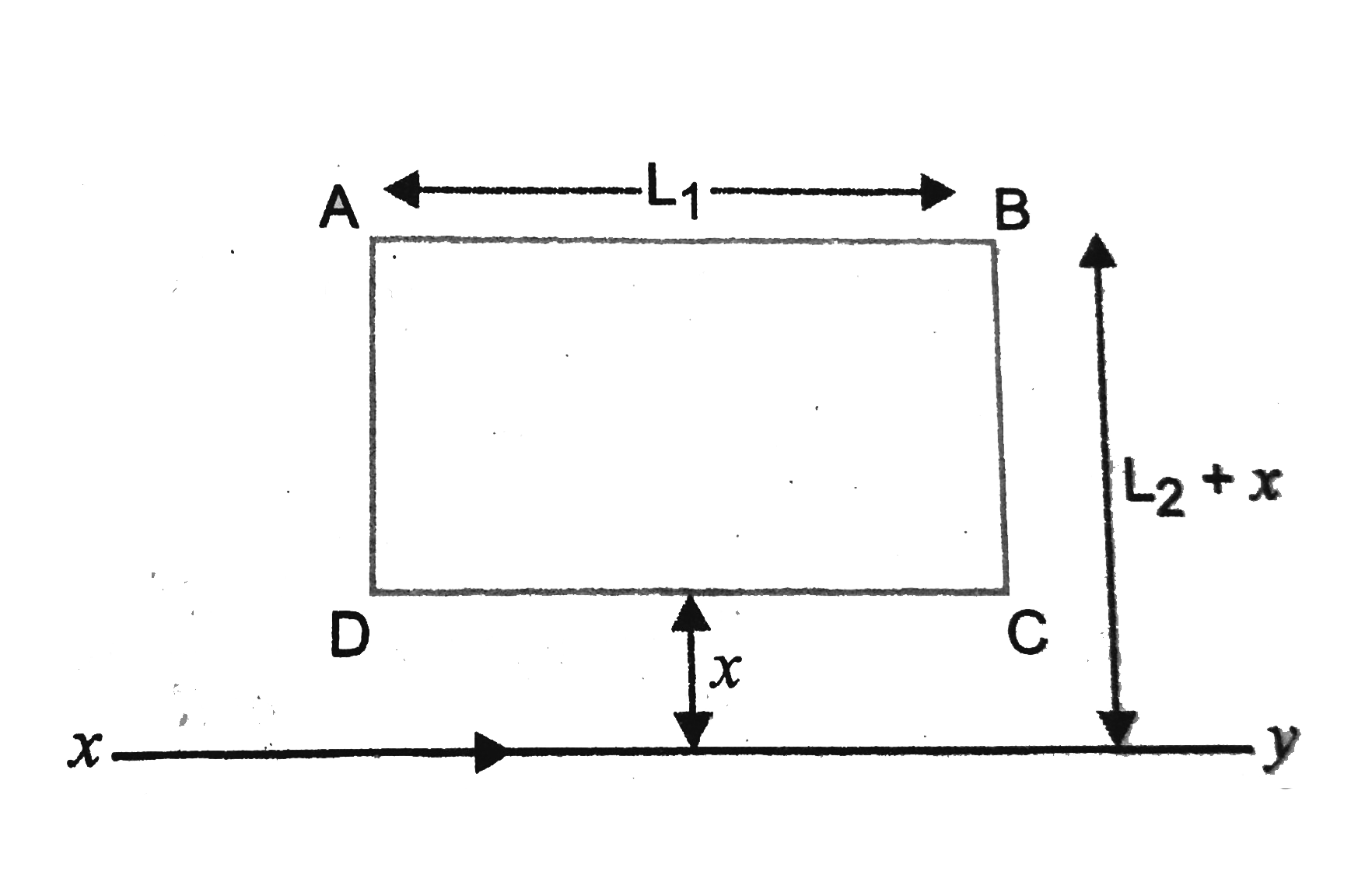
Consider an infinitely long wire carrying a current I (t),
With dIdt=λ = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig

Let us consider a strip of length l and width dr at a distance r from infinite long current carrying wire. The magnetic field at strip due to current carrying wire is given by Field B(r)=μ0I2πr (out of paper)
Total flux through the loop is Flux =μ0I2πl∫xxOdrr=μoI2πInxxo......(i)
The emf induced canbe obtained by differentiating the eq. (i) wrt t and then applying Ohm's law
εR=I
We have, induced current =1Rdϕdt=εR=μ0I2πλRInxx0
(∵dIdt=λ).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2iA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
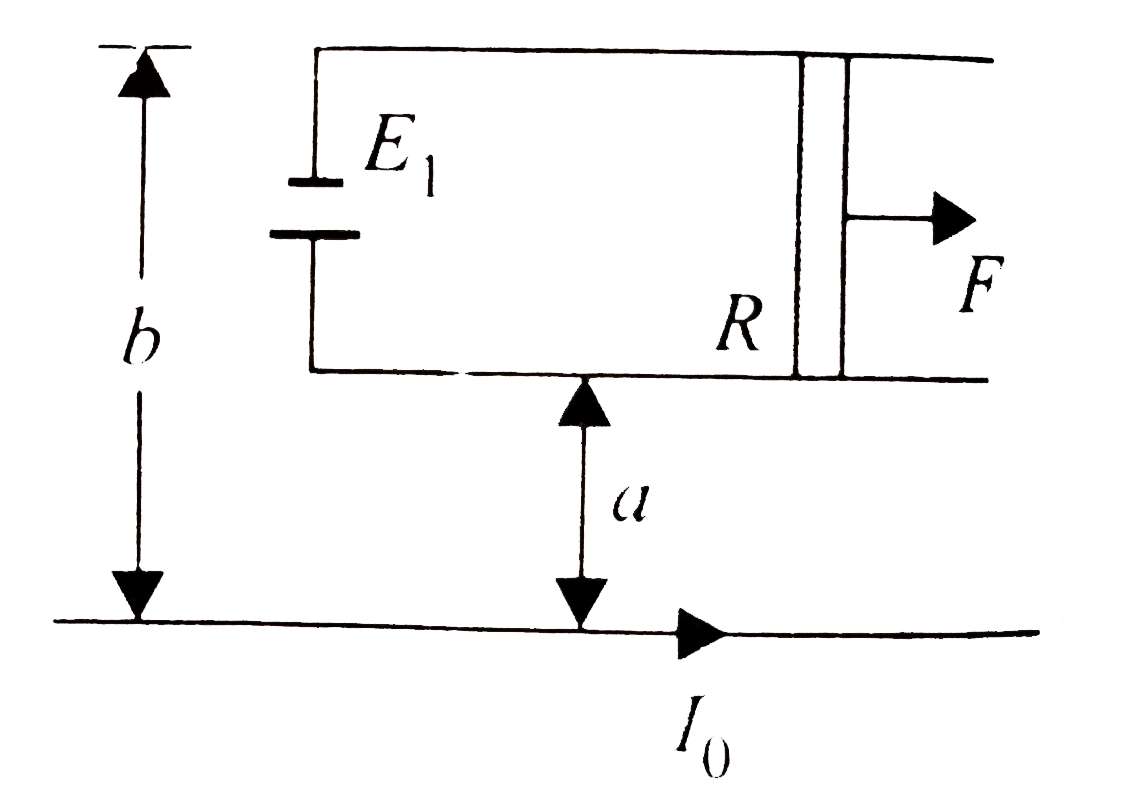
Find the value of current in the circuit if the rod slides with constant velocity v0A1R{E−μ0I0v02π1n∣∣∣ba∣∣∣}B1R{E+μ0I0v02π1n∣∣∣ba∣∣∣}C1R{E−μ0I0v0π1n∣∣∣ba∣∣∣}DNone of theseAn infinitely long straight wire is carrying a current I1. Adjacent to it there is another equilateral triangular wire having current I2. Choose the wrong options
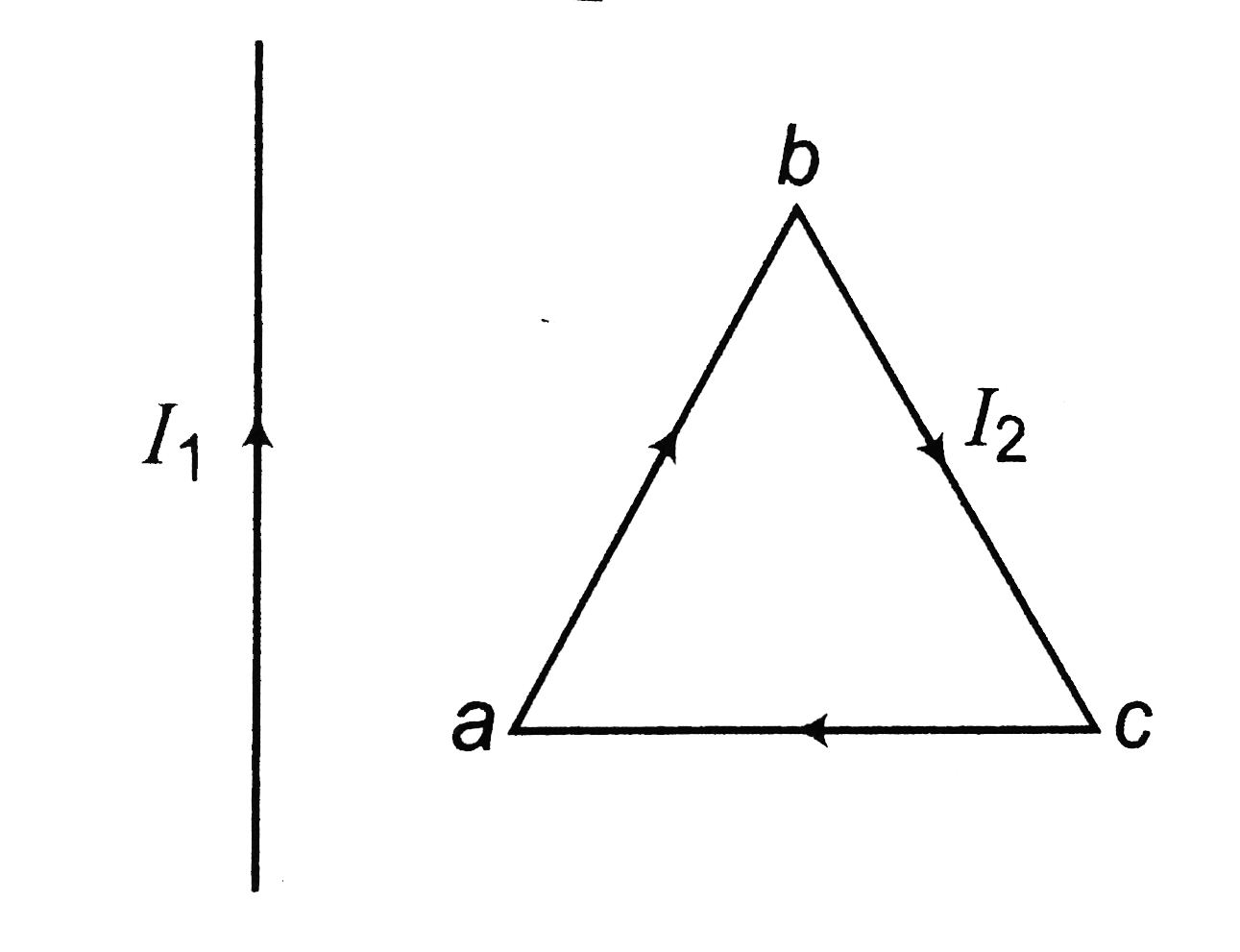 Anet force on loop is leftwardsBnet force on loop is rilght wardsCnet force on loop is upwardsDnet force on loop is downwards
Anet force on loop is leftwardsBnet force on loop is rilght wardsCnet force on loop is upwardsDnet force on loop is downwards
A rectangular loop of wire ABCD is kept close to an infinitely long wire carring a current I (t) =I0(1=t/T) for 0≤t≤ and I (0) for t gt T, Fig. Find the total charges passing through a given point in the loop, in time T. resistance of the loop is R
View SolutionIn Fig. 30-45 , a rectangular loop of wire with length a= 2.2 cm, width b = 0.80 cm, and resistance R = 0.40 mn is placed near an infinitely long wire carrying current i = 4.7 A. The loop is then moved away from the wire at constant speed v = 3.2 mm/s. When the center of the loop is at distance r = 1.5b, what are (a) the magnitude of the magnetic flux through the loop and (b) the current induced in the loop?
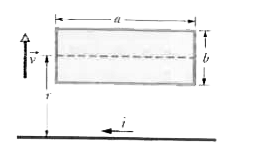
View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.

View SolutionA rectangular loop of length 'l' and breadth 'b' is placed at a distance of x from an infinitely long wire carrying current 'i' such that the direction of current is parallel to breadth. If the loop moves away from the current wire in a direction perpendicular to it with a velocity 'v', the magnitude of the e.m.f. in the loop is: (μ0= permeability of free space)
View SolutionConsider the magnetic field produced by a finitely long current carrying wire .
View Solution


