Consider a metal ring kept on top of a fixed solenoid (say on a carboard) The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on then
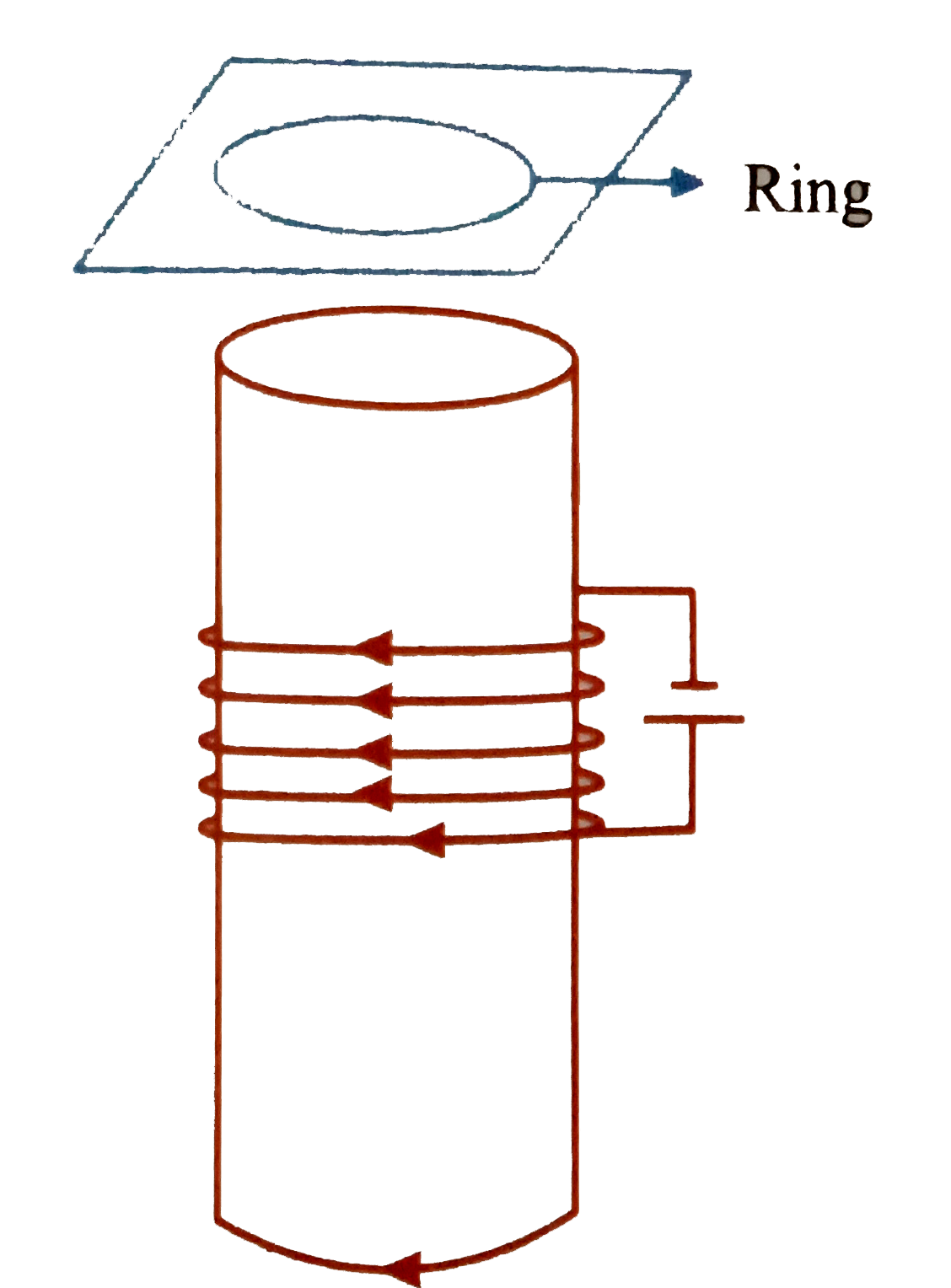
When the current is switched on, magnetic flux is linked through the ring. Thus, increases in flux takes place, According to Lenz's law, this increse in flux will be opposed and it can happen in the ring moves away from the solenoid.
This happen because the flux increases will cause a counter clockwise current (as seen from the top in the ring in figure .)i.e., opposite direction to that in the solenoid.
This makes the same sense of flow of current in the ring (when viewed form the bottom of the ring ) and solenoid forming same magnetic pole infront of each other. Hence, they will repel each other and the ring will move upward.
Topper's Solved these Questions
Similar Questions
Consider a metal ring kept on top of a fixed solenoid (say on a cardboard) as shown in Fig. 6.28. The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on, the metal ring jumps up. Explain.
View SolutionConsider a metal ring kept (supported by a cardboard) on top of a fixed solenoid carrying a current I (refer to the figure given in previous question). The centre of the ring coincides with the axis of the solenoid. If the current in the solenoid is switched off, what will happen to the ring?
View Solution
Knowledge Check
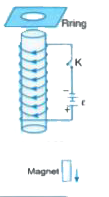
Consider metal ring kept on a horizontal plane . A bar magnet is held above the ring with its length along the axis is held above the ring with its length along the axis of the ring . If the magnet is dropped freely the acceleration of the falling magnet is : ( g is accelration due to gravity )
AMore than gBEqual to gCLess than gDDepends on mass of magnetThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
 A(2M+L)I0RBMI0RC(2M−L)I0RD(M+L)I0R
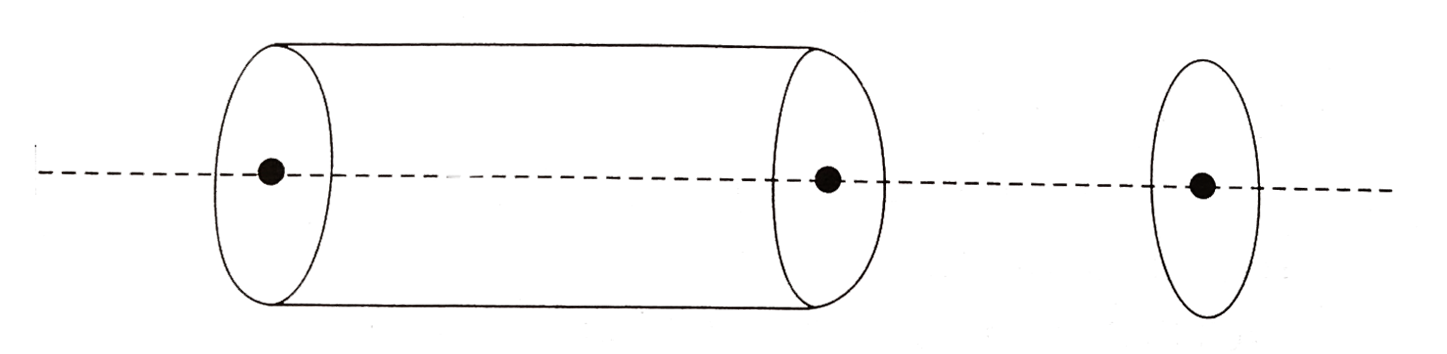
A(2M+L)I0RBMI0RC(2M−L)I0RD(M+L)I0RA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centreAdIdt=Rμ0niIBdIdt=−2Rπμ0a2ICdIdt=−2Rμ0a2IDNone of these
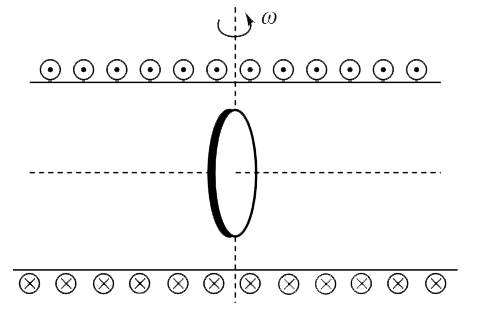
A long solenoid has n turns per unit length and carries a current i=i0sinωt. A coil of N turns and area A is mounted inside the solenoid and is free to rotate about its diameter that is perpendicular to the axis of the solenoid. The coil rotates with angular speed ω and at time t = 0 the axis of the coil coincides with the axis of the solenoid as shown in figure. Write emf induced in the coil as function of time.
View SolutionA tightly- wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surgace current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
View SolutionThe cruuent in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/s and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View SolutionA long solenoid of diameter 0.1m has 2×104 turns per metre. At the centre of the solenoid, a coil of 100 turns and radius 0.01m is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to 0A from 4A in 0.05 .If the resistance of the coil is 10π2ohm, the total charge (in μC ) flowing through the coil during this time is
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.01As−1. The solenoid has 2000 turns/m and its radius 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds. (b) find the electric field induced at a point on the circumference of the circle. (c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View Solution
