Determine the maximum value of Z=11x+7y subject to the constraints
Video Solution
Text Solution
The correct Answer is:N/a
We have maximise Z=11x+7y …(i)
Subject to the constraints
We see that, the feasible region as shaded determined by the system of constraints (ii) to (iv) is OABC and is bounded. So, now we shall corner point method to determine the maximum value of Z.
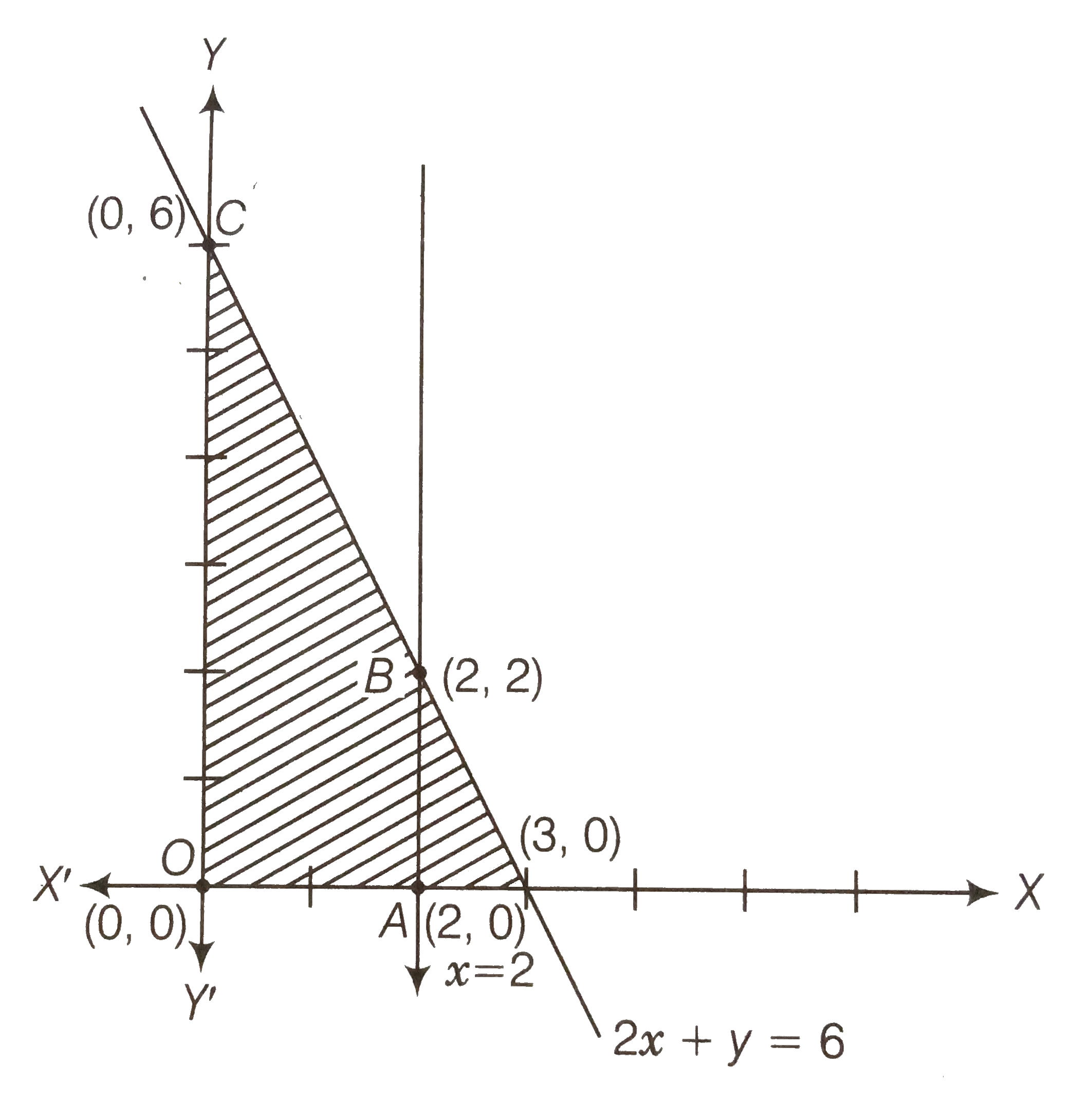

|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The maximum value of Z=3x+4y subject to the constraints:
x+y≤4,x≥0,y≥0 is :A0B12C16D18The maximum value of Z=9x+13y subject to constraints 2x+3y≤18,2x+y≤10,x≥0,y≥0, is
A130B81C79D99The maximum value of Z=3x+5ysubjected to the constraints x+y≤2,4x+3y≤12,x≥0,y≥0 is
A10B9C15D20
Maximise the function Z=11x+7y, subject to the constraints x≤3,y≤2,x≥0,y≥0
View SolutionThe point at which the maximum value of Z=4x+6y subject to the constraints 3x+2y≤12,x+y≥4,x≥0,y≥0 is obtained at the point
View SolutionThe maximum value of Z = 4x + 2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
View SolutionThe minimum value of Z= 4x+5y subject to the constraints x≤30,y≤40 and x≥0,y≥0 is
View SolutionThe maximum vlaue of Z=9x+13y subject to constraints 2x+3y≤18,2x+y≤10,x≥0,y≥0 is
View Solution